7. Электронные таблицы

Ниже приведен фрагмент электронной таблицы. Определите значение \(D3\), если в нее скопировать формулу из ячейки \(D2\). Знак \(\$\) означает абсолютную адресацию.
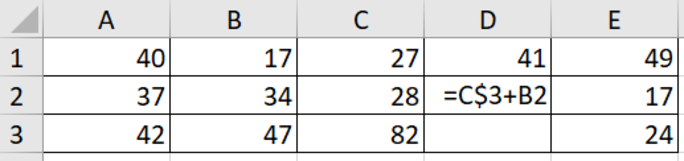
В ячейке \(D2\) записана формула \(=C\$3+B2\). Посмотрим, что произойдет с каждым из слагаемых в формуле при копировании ячейки вниз.
Абсолютная адресация означает, что при копировании то, что стоит после знака абсолютной адресации (причем только один символ, то есть в \(\$C1\) абсолютная адресация распространяется только на \(C\), а на 1 — уже относительная, то есть символ может меняться при копировании ячейки), замораживается и не меняется.
В \(C\$3\) для \(C\) адресация относительная, то есть при копировании ячейки \(C\) может измениться. Изменится ли? Копирование происходит на ячейку вниз, то есть столбик, в который идет копирование, не отличается от столбика, из которого идет.
При относительной адресации значение столбика в формуле изменяется на столько, на сколько изменяется значение столбика, куда копируем, относительно ячейки, из которой это делаем. В данном случае столбик не изменился, значит, остается \(C\).
\(\$3\) — абсолютная адресация, поэтому так и остается 3 строчка. Значит, первое слагаемое не меняется.
Теперь рассмотрим второе. \(B2\) — относительная адресация и для \(B\), и для 2, значит, может измениться и то, и то. Как мы поняли ранее, столбик не меняется, поэтому не меняется и \(B\). А вот строчка меняется: мы опускаемся на одну вниз, значит, и в формуле значение поменяется на единицу больше. Тогда \(B2\) превращается в \(B3\).
Таким образом, для \(D3\) формула имеет вид \(=C\$3 + B3\). Подставим значения из таблицы: \(= 82 + 47 = 129\).
Ниже приведен фрагмент электронной таблицы. Определите значение \(B1\), если в нее скопировать формулу из ячейки \(D3\). Знак \(\$\) означает абсолютную адресацию.
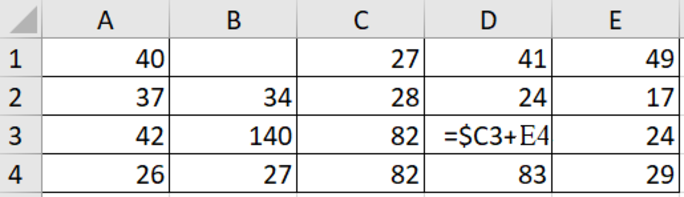
В ячейке \(D3\) записана формула \(=\$C3+E4\). Посмотрим, что произойдет с каждым из слагаемых в формуле при копировании ячейки в \(B1\).
Абсолютная адресация означает, что при копировании то, что стоит после знака абсолютной адресации (причем только один символ, то есть в \(\$Q1\) абсолютная адресация распространяется только на \(Q\), а на 1 — уже относительная, то есть символ может меняться при копировании ячейки), замораживается и не меняется.
В \(\$С3\) для 3 адресация относительная, то есть при копировании ячейки 3 может измениться.
При относительной адресации значение столбика в формуле изменяется на столько, на сколько изменяется значение столбика, куда копируем, относительно ячейки, из которой это делаем. Копирование происходит на две строки вверх, то есть значение строки уменьшится на 2. Значит, 3 уменьшится на 2 — и станет 1.
\(\$C\) — абсолютная адресация, поэтому так и остается столбик \(C\). Значит, первое слагаемое — это \(\$C1\).
Теперь рассмотрим второе. \(E4\) — относительная адресация и для \(E\), и для 4, значит, может измениться и то, и то. Мы поднимаемся на две строчки вверх и смещаемся на два столбика влево, то есть и то, и то уменьшается на 2: \(E\) становится \(C\), 4 — становится 2. Значит, \(E4\) — теперь \(C2\).
Таким образом, для \(B1\) формула имеет вид \(=\$C1 + C2\). Подставим значения из таблицы: \(= 27 + 28 = 55\).
С помощью электронных таблиц строят таблицу значений формулы \(9y + 4x\), где \(x\) и \(y\) принимают целые значения от 11 до 15 (включительно: 11, 12, 13, 14, 15). Чтобы это сделать, в таблицу записали числа от 11 до 15 так: в \(A2:A6\) — значения \(y\), \(B1:F1\) — значения \(x\). После в \(B2\) записали формулу и скопировали ее во все ячейки диапазона \(B2:F6\), получив таблицу, приведенную ниже. Определите, какую формулу записали в \(B2\):
\(1) =9*\$A2+4*B1\\
2) =9*\$A2+4*B\$1\\
3) =9*A2+4*B\$1 \\
4) =9*\$A\$2+4*B\$1\)
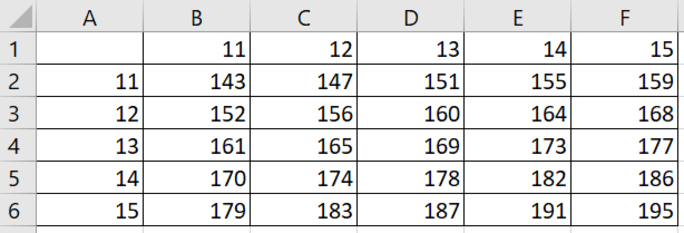
Запишем формулу для ячейки \(B2\). Нужно получить \(9y + 4x\). Значения \(y\) – в столбце \(A\), начиная с второй строки, \(x\) – в строке 1, начиная с столбца \(B\). Значит, формула имеет вид \(=9*A2 + 4*B1\). Но нам нужно, чтобы для значений y мы ссылались только на столбик \(A\) (иначе в какой-то момент мы будем ссылаться на неподходящий столбик \(B\), \(C\) и т.д.), а \(x\) – строчку 1 (аналогично: иначе в какой-то момент мы начнем ссылаться на строчку 2, 3 и т.д., где не те значения), поэтому для y нам нужно абсолютной ссылкой зафиксировать столбик \(A\), а для \(x\) – строчку 1. Тогда формула принимает вид \(=9*\$A2+4*B\$1\). Проверим руками (подставив значения), те ли значения принимаются по такой формуле для некоторых ячеек в таблице. Получаем, что значения действительно верные, значит, формула та.
В электронной таблице в ячейке \(K1\) записана формула \(=D4+\$C2+B\$3\). Определите, какой вид приобретет формула, если скопировать ячейку в \(K3\):
\(1) =D6+\$C4+B\$3\\
2) =D6+\$C3+B\$3\\
3) =D4+\$C4+B\$3\\
4) =D6+\$C4+B\$2\)
Рассмотрим, как изменится каждое слагаемое. В \(D4\) все ссылки относительные. Мы сдвигаемся на две ячейки вниз, не меняя столбик, значит, столбик не изменится, а строчка – да, станет на 2 единицы больше. Значит, \(D4 \rightarrow D6\).
В \(\$C2\) ссылка на \(C\) абсолютная, значит, столбик не изменится. Аналогично прошлому слагаемому, мы сдвигаемся на 2 строки вниз, значит, \(\$C2 \rightarrow \$C4\).
Аналогично \(B\$3 \rightarrow B\$3\): столбик не меняется, а ссылка на строчку абсолютная, потому значение строчки не меняется.
Формулу из ячейки \(K1\) скопировали в ячейку \(M7\). Значение ячейки \(M7\) вычисляется по формуле \(18x + 2y\) (\(x\) — значение ячейки \(C18\), \(y\) — \(M18\)). Определите формулу, записанную в ячейке \(K1\):
\(1) =18*A12+2*K12\\
2) =18*A24+2*K12\\
3) =18*A12+2*K24\\
4) =18*A12+2*M12\\\)
Значение ячейки \(M7\) вычисляется по формуле \(18x + 2y = 18 \cdot C18 + 2 \cdot M18\).
При копировании ячейки \(K1\) в \(M7\) значение столбика увеличивается на 2, а строки — на 6. Значит, в ячейке \(К1\) стояла формула \(=18*A12+2*K12\).
Формулу из ячейки \(K1\) скопировали в ячейку \(M7\). Значение ячейки \(M7\) вычисляется по формуле \(9x + 4y\) (\(x\) — значение ячейки \(C18\), \(y\) — \(M18\)). Определите формулу, записанную в ячейке \(K1\):
\(1) =9*A24+4*K12\\
2) =9*A12+4*K24\\
3) =9*A12+4*K12\\
4) =9*A12+4*N12\\\)
Значение ячейки \(M7\) вычисляется по формуле \(9x + 4y = 9 \cdot C18 + 4 \cdot M18\).
При копировании ячейки \(K1\) в \(M7\) значение столбика увеличивается на 2, а строки — на 6. Значит, в ячейке \(К1\) стояла формула \(=9*A12+4*K12\).
В ячейке \(A1\) записана формула \(=K\$1+A18\). Определите формулу, которая получится в ячейке \(D3\) при копировании из \(A1\):
\(1) =N\$1+D18\\
2) =N1+D20\\
3) =N\$3+D20\\
4) =N\$1+D20\\\)
Мы копируем из ячейки \(A1\) в ячейку \(D3\), то есть сдвигаемся на 3 столбца вправо и на 2 строки вниз.
Рассмотрим каждое слагаемое в формуле. \(K\$1\) — ссылка на \(K\) относительная, то есть столбик меняется: сдвигается на 3 вправо. Ссылка на 1 — абсолютная, то есть не меняется. Значит, \(K\$1 \rightarrow N\$1\).
В \(A18\) все ссылки относительные, то есть столбик сдвигается на 3 вправо, а строчка — на 2 вниз. Тогда \(A18 \rightarrow D20\).
Значит, формула имеет вид \(=N\$1+D20\).



