Простейший анализ диаграмм

На диаграмме отображено количество участников марафона из разных регионов России по предметам.
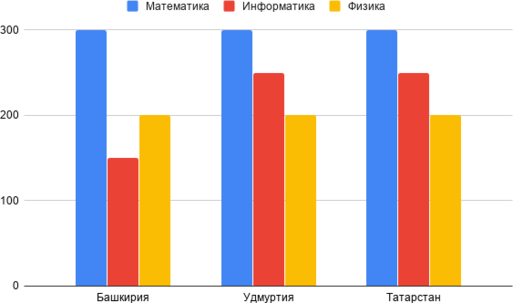
Какая из диаграмм правильно отражает соотношение общего количества участников (из всех трех регионов) по каждому из предметов?
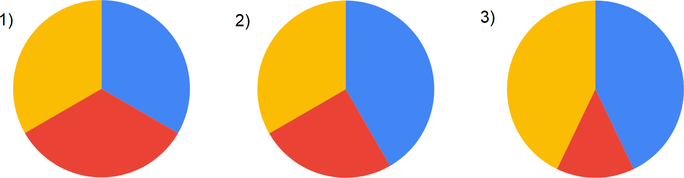
Так как на круговых диаграммах отображается процентное соотношение, вычислим его для наших данных, представленных в виде столбчатой диаграммы.
Для начала посчитаем общее количество участников по всем регионам и всем предметам: \(300+150+200+300+250+200+300+250+200=2150\)
Далее разделим суммарное количество участников марафона из региона на общее количество, которые мы нашли до этого:
Башкирия: \(150+250+350=750\)
\(750/2150=15/43\approx0.34\approx34\%\)
Удмуртия: \(300+250+200=750\)
\(750/2150=15/43\approx0.34\approx34\%\)
Татрстан: \(300+250+200=750\)
\(750/2150=15/43\approx0.34\approx34\%\)
Как мы можем заметить, процентные соотношения равны, значит и секторы диаграммы долдны быть равны, значит, наш ответ 1.
Дан фрагмент электронной таблицы:

Какое целое число должно быть записано в ячейке А1, чтобы диаграмма, построенная по значениям ячеек А2:С2, соответствовала рисунку? Известно, что все значения ячеек из рассматриваемого диапазона неотрицательны.
Для начала посчитаем значения формул в ячейках:
\(A2: x+6-3=x+3\)
\(B2: (5x+5)/5=x+1\)
\(C2: (x+1)*(x-4)=x^2-4x+x-4=x^2-3x-4\)
Из диаграммы видно, что секторы равны, значит, приравняем два любых уравнения и найдем ответ:
\(x^2-3x-4=x+1\)
\(x^2-4x-5=0\)
\(D=16+20=6^2\)
\(x_1=(4+6)/2=5\)
\(x_2=(4-6)/2=-1\)
Так как по условию все числа неотрицательные, наш ответ — 5.
Дан фрагмент электронной таблицы:

Какое целое число должно быть записано в ячейке А1, чтобы диаграмма, построенная по значениям ячеек А2:С2, соответствовала рисунку? Известно, что все значения ячеек из рассматриваемого диапазона неотрицательны.
Для начала посчитаем значения формул в ячейках:
\(A2: x+5-4=x+1\)
\(B2: (6x+6)/6=x+1\)
\(C2: (x+1)*(x-4)=x^2-4x+x-4=x^2-3x-4\)
Из диаграммы видно, что секторы равны, значит, приравняем два любых уравнения и найдем ответ:
\(x^2-3x-4=x+1\)
\(x^2-4x-5=0\)
\(D=16+20=6^2\)
\(x_1=(4+6)/2=5\)
\(x_2=(4-6)/2=-1\)
Так как по условию все числа неотрицательные, наш ответ — 5.
Дан фрагмент электронной таблицы:

Какое целое число должно быть записано в ячейке C1, чтобы диаграмма, построенная по значениям ячеек А2:С2, соответствовала рисунку? Известно, что все значения ячеек из рассматриваемого диапазона неотрицательны.
Для начала посчитаем значения формул в ячейках:
\(A2: x-1\)
\(B2: (9+1)/5=2\)
\(C2: 2x\)
Из диаграммы видно, что секторы равны, значит, приравняем два любых уравнения и найдем ответ:
\(2x=2\)
\(x=1\)
Дан фрагмент электронной таблицы:

Какое целое число должно быть записано в ячейке С1, чтобы диаграмма, построенная по значениям ячеек A2:C2, соответствовала рисунку? Известно, что все значения ячеек из рассматриваемого диапазона неотрицательны.
Для начала посчитаем значения формул в ячейках:
\(A2: x+3\)
\(B2: (4x-4)/4=x-1\)
\(C2: 7x\)
Из диаграммы видно, что секторы равны, значит, приравняем два любых уравнения и найдем ответ:
\(7x=x+3\)
\(6x=3\)
\(x=2\)


