Описанная окружность (страница 5)

Рассмотрим картинку:

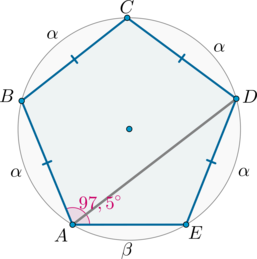
Т.к. равные хорды стягивают равные дуги, то меньшие полуокружности дуги \(\buildrel\smile\over{AB}\), \(\buildrel\smile\over{BC}\), \(\buildrel\smile\over{CD}\), \(\buildrel\smile\over{DE}\) равны:

\[\buildrel\smile\over{AB}=\buildrel\smile\over{BC}= \buildrel\smile\over{CD}=\buildrel\smile\over{DE}=\alpha.\]

Следовательно, \(\angle A=\frac12\cdot 3\alpha=97,5^\circ \quad \Rightarrow \quad \alpha=65^\circ\).

Т.к. градусная мера всей окружности равна \(360^\circ\), то

\[4\alpha+\beta=360^\circ \quad \Rightarrow \quad \beta=100^\circ\]

Тогда вписанный \(\angle ADE=\frac12\beta=50^\circ\).

Рассмотрим картинку:

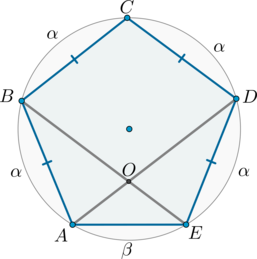
1) Т.к. равные хорды стягивают равные дуги, то меньшие полуокружности дуги \(\buildrel\smile\over{AB}\), \(\buildrel\smile\over{BC}\), \(\buildrel\smile\over{CD}\), \(\buildrel\smile\over{DE}\) равны:

\[\buildrel\smile\over{AB}=\buildrel\smile\over{BC}= \buildrel\smile\over{CD}=\buildrel\smile\over{DE}=\alpha.\]

Пусть также \(\buildrel\smile\over{EA}=\beta\).

2) \(\angle CBE=\frac12(\alpha+\alpha)=\alpha\), \(\angle BCD=\frac12(\alpha+\beta+\alpha)=\alpha+\frac12\beta\). Следовательно, \(\angle CBE+\angle BCD=2\alpha+\frac12\beta\).

Заметим, что вся окружность равна \(360^\circ\), следовательно, \(4\alpha+\beta=360^\circ\), откуда \(2\alpha+\frac12\beta=180^\circ\). Таким образом, \(\angle CBE\) и \(\angle BCD\) – односторонние углы при прямых \(CD\) и \(BE\) и секущей \(BC\). Следовательно, \(CD\parallel BE\).

Аналогично доказывается, что \(AD\parallel BC\).

3) Значит, \(BCDO\) – параллелограмм (\(BO\parallel CD, BC\parallel OD\)). А в параллелограмме противоположные стороны равны, следовательно, \(BO=CD=3\).

Рассмотрим картинку:

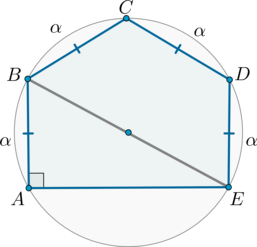
Т.к. равные хорды стягивают равные дуги, то меньшие полуокружности дуги \(\buildrel\smile\over{AB}\), \(\buildrel\smile\over{BC}\), \(\buildrel\smile\over{CD}\), \(\buildrel\smile\over{DE}\) равны:

\[\buildrel\smile\over{AB}=\buildrel\smile\over{BC}= \buildrel\smile\over{CD}=\buildrel\smile\over{DE}=\alpha.\]

Следовательно, \(\angle A=90^\circ=\frac32\alpha\), откуда \(\alpha=60^\circ\).

Значит, вписанный \(\angle AEB=\frac12\alpha=30^\circ\). Следовательно, из прямоугольного треугольника \(AEB\)

\[\mathrm{tg}\,30^\circ=\dfrac{AB}{AE} \quad \Rightarrow \quad AE=12.\]

Рассмотрим картинку:

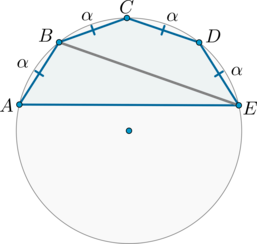
Т.к. равные хорды стягивают равные дуги, то меньшие полуокружности дуги \(\buildrel\smile\over{AB}\), \(\buildrel\smile\over{BC}\), \(\buildrel\smile\over{CD}\), \(\buildrel\smile\over{DE}\) равны:

\[\buildrel\smile\over{AB}=\buildrel\smile\over{BC}= \buildrel\smile\over{CD}=\buildrel\smile\over{DE}=\alpha.\]

Следовательно, \(\angle A=45^\circ=\frac32\alpha\), откуда \(\alpha=30^\circ\).

Значит, вписанный \[\angle ABE=\frac12\buildrel\smile\over{AE}= \frac12\left(360^\circ-4\alpha\right)=120^\circ\]

Тогда, т.к. \(\triangle ABE\) – вписанный, то \(\dfrac{AE}{\sin \angle B}=2R\), где \(R\) – радиус данной окружности. Следовательно:

\[\dfrac{AE}{\sin \angle B}=2R \quad \Rightarrow \quad R=6.\]

Рассмотрим картинку:

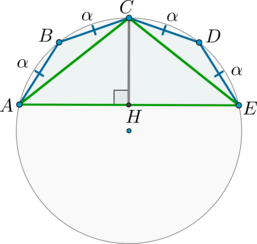
Т.к. равные хорды стягивают равные дуги, то меньшие полуокружности дуги \(\buildrel\smile\over{AB}\), \(\buildrel\smile\over{BC}\), \(\buildrel\smile\over{CD}\), \(\buildrel\smile\over{DE}\) равны:

\[\buildrel\smile\over{AB}=\buildrel\smile\over{BC}= \buildrel\smile\over{CD}=\buildrel\smile\over{DE}=\alpha.\]

Следовательно, \(\angle A=45^\circ=\frac32\alpha\), откуда \(\alpha=30^\circ\).

Тогда \(\angle CAE=\frac12\cdot 2\alpha=30^\circ\).

Заметим, что \(\triangle ACE\) – равнобедренный (\(\angle A=\angle E=\alpha\)), следовательно, \(CH\) – высота и медиана, то есть \(AH=\frac12\cdot AE=4\sqrt3\). Значит:

\[\mathrm{tg}\,30^\circ=\dfrac{CH}{AH} \quad \Rightarrow \quad CH=4.\]

Рассмотрим картинку:

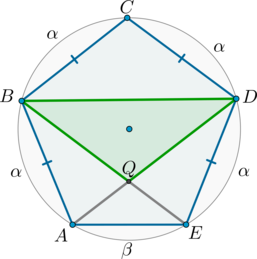
1) Т.к. равные хорды стягивают равные дуги, то меньшие полуокружности дуги \(\buildrel\smile\over{AB}\), \(\buildrel\smile\over{BC}\), \(\buildrel\smile\over{CD}\), \(\buildrel\smile\over{DE}\) равны:

\[\buildrel\smile\over{AB}=\buildrel\smile\over{BC}= \buildrel\smile\over{CD}=\buildrel\smile\over{DE}=\alpha.\]

Пусть также \(\buildrel\smile\over{EA}=\beta\).

2) \(\angle CBE=\frac12(\alpha+\alpha)=\alpha\), \(\angle BCD=\frac12(\alpha+\beta+\alpha)=\alpha+\frac12\beta\). Следовательно, \(\angle CBE+\angle BCD=2\alpha+\frac12\beta\).

Заметим, что градусная мера всей окружности равна \(360^\circ\), следовательно, \(4\alpha+\beta=360^\circ\), откуда \(2\alpha+\frac12\beta=180^\circ\). Таким образом, \(\angle CBE\) и \(\angle BCD\) – односторонние углы при прямых \(CD\) и \(BE\) и секущей \(BC\). Следовательно, \(CD\parallel BE\).

Аналогично доказывается, что \(AD\parallel BC\).

3) Значит, \(BCDQ\) – параллелограмм (\(BQ\parallel CD, BC\parallel QD\)). А в параллелограмме противоположные стороны равны, следовательно, \(BQ=CD=BC=DQ\). То есть \(BCDQ\) – ромб.

4) Таким образом, \(\triangle BCD=\triangle BQD\). Значит, и радиусы описанных около этих треугольников окружностей равны. Но радиус описанной около \(\triangle BCD\) окружности равен радиусу описанной около пятиугольника \(ABCDE\) окружности. Следовательно, ответ \(5\).

Так как трапеция вписана в окружность, то трапеция является равнобедренной, следовательно, \(AB=CD\). Средняя линия равна полусумме оснований, следовательно, \(AD+BC=2\cdot 5=10\). Тогда \[AB+BC+CD+AD=10+2AB=22\quad\Rightarrow\quad AB=6.\]