Радиус, длина и центр окружности (страница 2)

В окружности с центром \(O\) \(AC\) и \(BD\) – диаметры. Центральный угол \(AOD\) равен \(110^\circ\). Найдите вписанный угол \(ACB\). Ответ дайте в градусах.
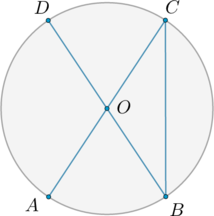
Так как \(BD\) – диаметр, то \(\angle BOD=180^\circ\), следовательно, \(\angle AOB=180^\circ-\angle AOD=70^\circ\). \(\angle AOB\) и \(\angle ACB\) – центральный и вписанный углы соответственно, опирающиеся на одну и ту же дугу, следовательно, \(\angle ACB=\angle AOB:2=35^\circ\).
Четырехугольник \(ABCD\) вписан в окружность. Угол \(ABC\) равен \(105^\circ\), угол \(CAD\) равен \(35^\circ\). Найдите угол \(ABD\). Ответ дайте в градусах.
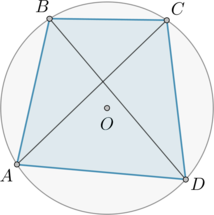
Так как вписанный угол равен половине дуги, на которую он опирается, то \(\buildrel\smile\over{CDA}\,=2\cdot 105^\circ=210^\circ\). Аналогично меньшая дуга \(\buildrel\smile\over{CD}\,=2\cdot 35^\circ=70^\circ\) (см.рис.). Следовательно, меньшая дуга \(\buildrel\smile\over{AD}\,=210^\circ-70^\circ=140^\circ\) (см.рис.). Значит \(\angle ABD\), как вписанный и опирающийся на дугу, равную \(140^\circ\), сам равен \(70^\circ\).
Четырехугольник \(ABCD\) вписан в окружность. Угол \(ABD\) равен \(75^\circ\), угол \(CAD\) равен \(35^\circ\). Найдите угол \(ABC\). Ответ дайте в градусах.

Так как вписанный угол равен половине дуги, на которую он опирается, то меньшая \(\buildrel\smile\over{DA}\,=2\cdot 75^\circ=150^\circ\) (см.рис.). Аналогично меньшая дуга \(\buildrel\smile\over{CD}\,=2\cdot 35^\circ=70^\circ\) (см.рис.). Следовательно, дуга \(\buildrel\smile\over{CDA}\,=150^\circ+70^\circ=220^\circ\). Значит \(\angle ABC\), как вписанный и опирающийся на дугу, равную \(220^\circ\), сам равен \(110^\circ\).
Точки \(A\) и \(C\) разбивают окружность на две дуги, одна из которых равна \(280^\circ\) и на которой отмечена точка \(B\). Найдите угол \(BAC\), если \(AB=AC\). Ответ дайте в градусах.
Рассмотрим картинку:

\(\buildrel\smile\over{ABC}=280^\circ\), следовательно, меньшая дуга \(\buildrel\smile\over{AC}=360^\circ-280^\circ=80^\circ\). Т.к. угол \(ABC\) опирается на эту дугу и является вписанным, то он равен ее половине, то есть \(40^\circ\).
Заметим, что \(\triangle ABC\) – равнобедренный, следовательно, \(\angle BAC=180^\circ-2\cdot 40^\circ=100^\circ\).
Точки \(A\) и \(B\) делят окружность на две дуги, одна из которых равна \(170^\circ\), а другая точкой \(K\) делится в отношении \(11:8\), считая от точки \(A\). Найдите \(\angle BAK\). Ответ дайте в градусах.
Рассмотрим картинку:
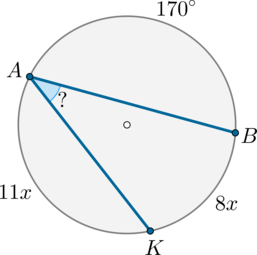
Т.к. \(\buildrel\smile\over{AK}:\buildrel\smile\over{KB}=11:8\), то можно обозначить \(\buildrel\smile\over{AK}=11x, \buildrel\smile\over{KB}=8x\).
Дуга \(\buildrel\smile\over{AKB}=360^\circ -170^\circ=190^\circ\). Следовательно, \(11x+8x=19x=190^\circ \quad \Rightarrow \quad x=10^\circ\). Значит, дуга \(\buildrel\smile\over{KB}=8x=80^\circ\). Угол \(BAK\) вписанный и опирается на эту дугу, следовательно, он равен ее половине, то есть \(40^\circ\).
На окружности в следующем порядке отмечены четыре точки: \(A\), \(B\), \(C\) и \(D\), причем \(AB=BC, \ CD=DA\). Найдите угол \(BAD\). Ответ дайте в градусах.
Рассмотрим картинку:
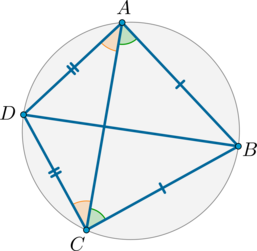
Т.к. \(\triangle BAC\) и \(DAC\) – равнобедренные, то \(\angle BAC=\angle BCA, \ \angle DAC=\angle DCA\). Таким образом, \(\angle A=\angle C\).
Т.к. \(\angle A, \angle C\) – вписанные, то \(\angle A+\angle
C=\frac12\left(\buildrel\smile\over{DCB}+\buildrel\smile\over{DAB}\right)\).
Заметим, что эти дуги в сумме дают всю окружность, то есть \(360^\circ\). Следовательно, \(\angle A+\angle C=180^\circ\), следовательно, \(\angle A=\angle C=90^\circ\).
Секущая \(AB\) пересекает окружность и диаметр \(CD\) так, как показано на рисунке.
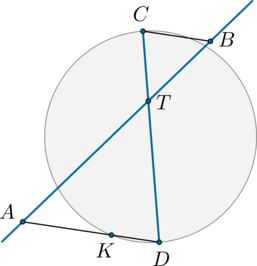
Меньшая дуга \(\buildrel\smile\over{KD}\) равна \(40^\circ\), \(\angle CBA=30^\circ\), прямая \(BC\) параллельна прямой \(AD\). Найдите угол \(BTD\). Ответ дайте в градусах.
Рассмотрим картинку:
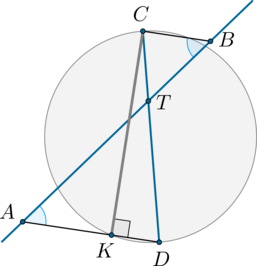
Т.к. \(BC\parallel AD\), то \(\angle CBT=\angle DAT=30^\circ\). \(\angle DCK\), как вписанный и опирающийся на дугу \(KD\), равен ее половине, то есть \(20^\circ\). \(\angle CKD\) опирается на диаметр \(CD\), следовательно, равен половине от половины окружности, то есть \(90^\circ\). Значит, \(\angle CDK=180^\circ -90^\circ -20^\circ=70^\circ\).
\(\angle BTD\) — внешний угол для треугольника \(ATD\), следовательно, он равен сумме двух углов треугольника, не смежных с ним: \(\angle BTD=\angle TDA+\angle TAD=30^\circ+70^\circ=100^\circ\).



