Вписанная окружность (страница 3)

Окружность вписана в угол \(B\), равный \(90^\circ\), причем \(A,C\) – точки касания окружности со сторонами этого угла. Найдите \(AC\), если радиус этой окружности равен \(5\sqrt2\).
Пусть \(O\) – центр окружности.
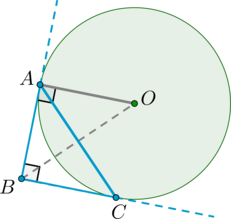
\(OA=5\sqrt2\) – радиус окружности, причем \(OA\perp BA\) (т.к. \(BA\) – касательная, а радиус, проведенный в точку касания, перпендикулярен касательной).
Т.к. окружность вписана в угол, то ее центр лежит на биссектрисе этого угла, то есть \(\angle ABO=45^\circ\). Тогда прямоугольный \(\triangle ABO\) является равнобедренным, то есть \(AB=OA=5\sqrt2\). Т.к. отрезки касательных, проведенных из одной точки к окружности, равны, то \(BC=AB=5\sqrt2\). Следовательно, по теореме Пифагора
\[AC=\sqrt{AB^2+BC^2}=\sqrt{2AB^2}=AB\cdot \sqrt2=5\sqrt2\cdot \sqrt2=10.\]
Окружность вписана в угол \(B\), равный \(90^\circ\), причем \(A,C\) – точки касания окружности со сторонами этого угла. Найдите площадь треугольника \(ABC\), если радиус этой окружности равен \(10\sqrt2\).
Пусть \(O\) – центр окружности.
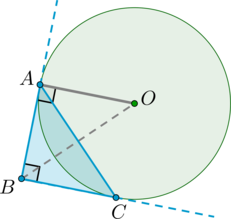
\(OA=10\sqrt2\) – радиус окружности, причем \(OA\perp BA\) (т.к. \(BA\) – касательная, а радиус, проведенный в точку касания, перпендикулярен касательной).
Т.к. окружность вписана в угол, то ее центр лежит на биссектрисе этого угла, то есть \(\angle ABO=45^\circ\). Тогда прямоугольный \(\triangle ABO\) является равнобедренным, то есть \(AB=OA=10\sqrt2\). Т.к. отрезки касательных, проведенных из одной точки к окружности, равны, то \(BC=AB=10\sqrt2\). Следовательно, площадь прямоугольного треугольника \(ABC\) равна
\[S_{\triangle ABC}=\dfrac12\cdot AB\cdot BC=\dfrac12\cdot 10\sqrt2\cdot 10\sqrt2= 100.\]
Окружность вписана в угол \(B\), равный \(90^\circ\). Найдите расстояние от вершины угла до центра этой окружности, если радиус этой окружности равен \(\sqrt2\).
Обозначим одну из точек касания окружности и сторон угла за \(A\). Пусть также \(O\) – центр окружности. То есть необходимо найти \(OB\).
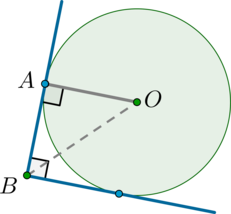
\(OA=\sqrt2\) – радиус окружности, причем \(OA\perp BA\) (т.к. \(BA\) – касательная, а радиус, проведенный в точку касания, перпендикулярен касательной).
Т.к. окружность вписана в угол, то ее центр лежит на биссектрисе этого угла, то есть \(\angle ABO=45^\circ\). Тогда прямоугольный \(\triangle ABO\) является равнобедренным, то есть \(AB=OA=\sqrt2\). По теореме Пифагора:
\[OB=\sqrt{OA^2+AB^2}=\sqrt{\sqrt2^{\,2}+\sqrt2^{\,2}}=2.\]
Окружность вписана в угол \(B\), равный \(60^\circ\). Найдите расстояние от вершины угла до центра этой окружности, если расстояние между точками касания окружности и сторон угла равно \(2\sqrt3\).
Обозначим точки касания окружности и сторон угла за \(A\) и \(C\). Тогда известно, что \(AC=2\sqrt3\). Пусть также \(O\) – центр окружности. То есть необходимо найти \(OB\).
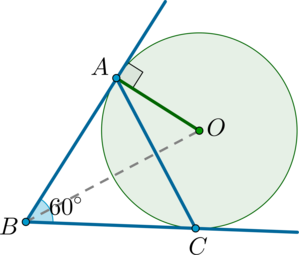
\(OA\) – радиус окружности, причем \(OA\perp BA\) (т.к. \(BA\) – касательная, а радиус, проведенный в точку касания, перпендикулярен касательной).
Рассмотрим \(\triangle ABC\): он равнобедренный (\(AB=BC\) как отрезки касательных, проведенных из одной точки), следовательно, \(\angle A=\angle C=0,5\cdot(180^\circ-60^\circ)=60^\circ\). Таким образом, он равносторонний, следовательно, \(AB=AC=2\sqrt3\).
Т.к. окружность вписана в угол, то ее центр лежит на биссектрисе этого угла, то есть \(\angle ABO=30^\circ\). Тогда из прямоугольного \(\triangle ABO\):
\[\cos 30^\circ=\dfrac{BA}{OB}=\dfrac{2\sqrt3}{OB} \quad \Rightarrow \quad OB=2\sqrt3\cdot \dfrac2{\sqrt3}=4.\]
Окружность вписана в угол \(B\), равный \(60^\circ\). Найдите радиус этой окружности, если расстояние между точками касания окружности и сторон угла равно \(3\sqrt3\).
Обозначим точки касания окружности и сторон угла за \(A\) и \(C\). Тогда известно, что \(AC=3\sqrt3\). Пусть также \(O\) – центр окружности.
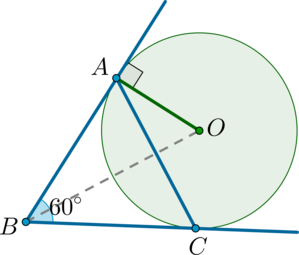
Тогда \(OA\) – радиус окружности, причем \(OA\perp BA\) (т.к. \(BA\) – касательная, а радиус, проведенный в точку касания, перпендикулярен касательной).
Рассмотрим \(\triangle ABC\): он равнобедренный (\(AB=BC\) как отрезки касательных, проведенных из одной точки), следовательно, \(\angle A=\angle C=0,5\cdot(180^\circ-60^\circ)=60^\circ\). Таким образом, он равносторонний, следовательно, \(AB=AC=3\sqrt3\).
Т.к. окружность вписана в угол, то ее центр лежит на биссектрисе этого угла, то есть \(\angle ABO=30^\circ\). Тогда из прямоугольного \(\triangle ABO\):
\[\mathrm{tg}\,30^\circ=\dfrac{OA}{BA}=\dfrac{OA}{3\sqrt3} \quad \Rightarrow \quad OA=3\sqrt3\cdot \dfrac{\sqrt3}3=3.\]
Окружность \(S\) касается стороны \(BC\) и продолжений сторон \(AB\) и \(AC\) треугольника \(ABC\). Найдите длину отрезка касательной к окружности \(S\), проведенной из точки \(A\), если периметр треугольника \(ABC\) равен \(20\).
Рассмотрим рисунок:
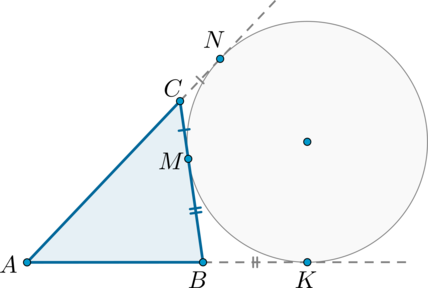
Т.к. отрезки касательных, проведенных из одной точки, равны, то \(CN=CM\), \(BM=BK\), \(AN=AK\). Таким образом, периметр
\(P=AC+CB+BA=AC+CM+MB+BA=AC+CN+BK+BA=\)
\(=(AC+CN)+(KB+BA)=AN+KA=2AN\)
Следовательно, \(AN=\frac12P=10\).
В треугольник вписана окружность радиуса \(2,4\sqrt3\). Одна из сторон треугольника равна \(13\), а разность двух других равна \(5\). Найдите большую сторону этого треугольника.
1) Пусть в треугольнике \(BC=13\), \(AC-AB=5\). Таким образом, наибольшей стороной будет или \(AC\), или \(BC\).
Т.к. отрезки касательных, проведенных из одной точки к окружности, равны, то \(AM=AK=a\), \(BM=BN=b\), \(CN=CK=c\) (где \(M,N,K\) – точки касания).
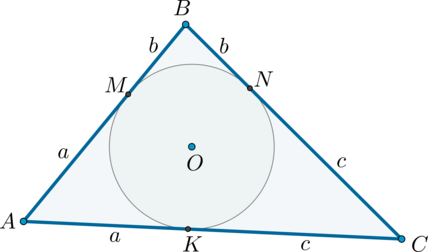
Таким образом, из условия следует, что \(b+c=13\), \(a+c-(a+b)=c-b=5\). Решая систему из этих двух уравнений, находим, что \(b=4\), \(c=9\).
2) Заметим, что полупериметр данного треугольника равен \(a+b+c=a+13\), а площадь по формуле Герона равна
\(S=\sqrt{(a+b+c)(a+b+c-(a+b))(a+b+c-(a+c))(a+b+c-(b+c))}=\)
\(=\sqrt{(a+b+c)\cdot a\cdot b\cdot c}=6\sqrt{a(a+13)}.\)
Тогда по формуле (площадь равна полупериметру, умноженному на радиус вписанной окружности) имеем:
\[S=(a+b+c)\cdot r \quad \Rightarrow \quad 6\sqrt{a(a+13)}= (a+13)\cdot 2,4\sqrt3 \quad \Rightarrow \quad 36a=(a+13)\cdot \left(\dfrac{12}5\sqrt3\right)^2,\]
откуда \(a=12\). Следовательно, \(AC=12+9=21>BC\). Значит, большая сторона равна \(21\).



