Нахождение приближенного значения корня

Одно из чисел \(\sqrt{40}, \sqrt{46}, \sqrt{53}, \sqrt{58}\) отмечено на прямой точкой \(A\).
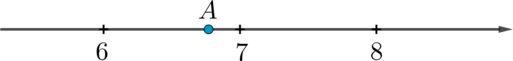
Какое это число?
1) \(\sqrt{40}\qquad \) 2) \(\sqrt{46}\qquad \) 3) \(\sqrt{53}\qquad \) 4) \(\sqrt{58}\)
Точка \(A\) лежит между числами \(6=\sqrt{36}\) и \(7=\sqrt{49}\). Между этими же числами находятся два числа \(\sqrt{40}\) и \(\sqrt{46}\), причем \(\sqrt{40}<6,5\), а \(\sqrt{46}>6,5\). Так как \(A\) лежит ближе к числу \(7\), то она соответствует числу \(\sqrt{46}\). Ответ 2.
Одно из чисел \(\sqrt{41}, \sqrt{48}, \sqrt{53}, \sqrt{63}\) отмечено на прямой точкой \(A\).

Какое это число?
1) \(\sqrt{41}\qquad \) 2) \(\sqrt{48}\qquad \) 3) \(\sqrt{53}\qquad \) 4) \(\sqrt{63}\)
Точка \(A\) лежит между числами \(7=\sqrt{49}\) и \(8=\sqrt{64}\). Между этими же числами находятся два числа \(\sqrt{53}\) и \(\sqrt{63}\), причем \(\sqrt{53}<7,5\), \(\sqrt{63}>7,5\). Так как \(A\) лежит ближе к числу \(7\), то она соответствует числу \(\sqrt{53}\). Ответ 3.
Одно из чисел \(\sqrt{28}, \sqrt{32}, \sqrt{39}, \sqrt{47}\) отмечено на прямой точкой \(A\).
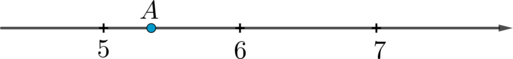
Какое это число?
1) \(\sqrt{28}\qquad \) 2) \(\sqrt{32}\qquad \) 3) \(\sqrt{39}\qquad \) 4) \(\sqrt{47}\)
Точка \(A\) лежит между числами \(5=\sqrt{25}\) и \(6=\sqrt{36}\). Между этими же числами находятся два числа \(\sqrt{28}\) и \(\sqrt{32}\), причем \(\sqrt{28}<5,5\), \(\sqrt{32}>5,5\). Так как \(A\) лежит ближе к числу \(5\), то она соответствует числу \(\sqrt{28}\). Ответ 1.
На координатной прямой отмечены точки \(A, B, C\) и \(D\). Одна из них соответствует числу \(\sqrt{95}\). Какая это точка?

1) \(A\qquad \) 2) \(B\qquad \) 3) \(C\qquad \) 4) \(D\)
Число \(\sqrt{95}\) находится между числами \(\sqrt{81}=9\) и \(\sqrt{100}=10\). Следовательно, это либо \(A\), либо \(B\). Так как \(\sqrt{95}>9,5\), то это точка \(B\) (потому что она находится правее середины отрезка \([9;10]\).
На координатной прямой отмечены точки \(A, B, C\) и \(D\). Одна из них соответствует числу \(\sqrt{33}\). Какая это точка?

1) \(A\qquad \) 2) \(B\qquad \) 3) \(C\qquad \) 4) \(D\)
Число \(\sqrt{33}\) находится между числами \(\sqrt{25}=5\) и \(\sqrt{36}=6\). Следовательно, это либо \(C\), либо \(D\). Так как \(\sqrt{33}>5,5\), то это точка \(D\) (потому что она находится правее середины отрезка \([5;6]\).
Какое из данных чисел принадлежит промежутку \([7;8]\)?
1) \(\sqrt 7\qquad \) 2) \(\sqrt 8\qquad \) 3) \(\sqrt{45}\qquad \) 4) \(\sqrt{60}\)
Так как \(7=\sqrt{49}\), \(8=\sqrt{64}\), то промежутку \([\sqrt{49}; \sqrt{64}]\) принадлежит число из пункта 4.
Какому промежутку принадлежит число \(\sqrt{89}\)?
1) \([8;9]\qquad \) 2) \([9;10]\qquad \) 3) \([10;11]\qquad \) 4) \([11;12]\)
Число \(\sqrt{89}\) лежит между числами \(\sqrt{81}=9\) и \(\sqrt{100}=10\). Следовательно, принадлежит промежутку \([9;10]\). Ответ 2.



