Электрический ток. Закон Ома (страница 3)

К аккумулятору с ЭДС \(\xi\) = 60 В и внутренним сопротивлением \(r \)= 5 Ом подключили лампу сопротивлением \(R_\text{ Л} =10\) Ом и резистор сопротивлением \(R =15\) Ом, а также конденсатор ёмкостью \(С = 80\) мкФ (см. рисунок). Спустя длительный промежуток времени ключ К размыкают. Какое количество теплоты выделится после этого на лампе? 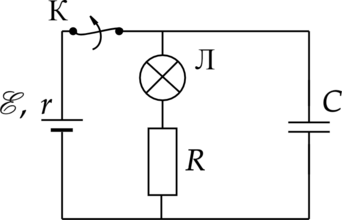
“Досрочная волна 2020 вариант 1”
Найдем по закону Ома для полной цепи силу тока \[I=\dfrac{\xi}{r+R_0}\] где \(\xi\) – ЭДС источника, \(r\) – внутреннее сопротивление источника, \(R_0\) – общее сопротивление цепи. \[R_0=10\text{ Ом}+15\text{ Ом}=25\text{ Ом}\] Значит, сила тока в цепи равна \[I=\dfrac{\xi}{r+R_0}=\dfrac{60\text{ В}}{5\text{ Ом}+25\text{ Ом}}=2 \text{ А}\] Значит напряжение на конденсаторе равно напряжению на участке с сопротивлением \(R_0\), то есть \[U_C=I R_0=2\text{ А} 25\text{ Ом}=50 \text{ В}\] А энергия на конденсаторе равна \[W=\dfrac{C U_C^2}{2}=\dfrac{80\text{ мкФ}\cdot 2500\text{ В$^2$}}{2}=100 \text{ мДж}\] Вся запасенная энергия будет расходоваться на резистор и лампу, при чем \[Q_1=I^2R \Delta t\hspace{5 mm} Q_\text{ Л}=I^2R_\text{ Л} \Delta t \hspace{5 mm} Q_1+Q_2=W\] где \(U\) – напряжения участка из лампы и резистора, \(Q_1\) и \(Q_2\) – выделяемая энергия на резисторе и лампе за время \(\Delta t\) соответственно.
Так как лампочка и резистор подключены последовательно, то \[\dfrac{Q_\text{ Л}}{Q_1}=\dfrac{R_\text{ Л}}{R}\] Отсюда энергия на лампочке \[Q_\text{ Л}=\dfrac{W}{1+\dfrac{R}{R_\text{ Л}}}=\dfrac{100\cdot 10^{-3}\text{ Дж}}{\dfrac{15\text{ Ом}}{10\text{ Ом}}}=40\text{ мДж}\]
В цепи изображённой на рисунке \(R_1=R_2=R_3=3\) Ом, \(r=0,5 \) Ом В начальный момент ключ K замкнут. Во сколько раз уменьшится мощность, выделяемая на \(R_1\) после размыкания ключа?
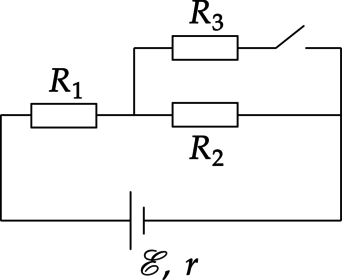
“Основная волна 2019”
Сила тока по закону Ома для полной цепи равна: \[I=\dfrac{\xi}{R_0+r}\] Общее сопротивление в первом и во втором случаях равно: \[R_{01}=R_1+\dfrac{R_2\cdot R_3}{R_3}=4,5\text{ Ом}\] \[R_{02}=R_1+R_2=6\text{ Ом}\] Мощность, выделяемая на резисторе, определяется формулой: \[P=I^2R\] То есть отношение мощностей: \[\dfrac{P_1}{P_2}=\dfrac{I_1^2}{I_2^2}=\left(\dfrac{R_{02}+r}{R_{01}+r}\right)^2=\left(\dfrac{6\text{ Ом}+0,5 \text{ Ом}}{4,5\text{ Ом}+0,5\text{ Ом}}\right)^2=1,69\]
Маша Комиссарова на лабораторной работе собирала цепь и провела 3 опыта с одним и тем же источником тока. В первом опыте к источнику тока подсоединила последовательно резистор с сопротивлением \(R_1=3\) Ом и измерила на нем силу тока, при этом она составила \(I_1=3\) Ом . Во втором опыте к источнику тока подсоединила резистор с сопротивлением \(R_2=5\) Ом и сила тока на нем составила \(I_2=2\) А. В третьем же опыте подсоединила блок из параллельных резисторов \(R_1\) и \(R_2\). Найдите какое значение силы тока должна была получить Маша в третьем случае.
Запишем закон Ома для случаев подключения ключа к 1 и 2 \[I_1=\dfrac{\xi}{R_1+r} \hspace{20 mm} I_2=\dfrac{\xi}{R_2+r}\] Здесь \(I_1\) и \(I_2\) — сила тока на резисторах 1 и 2, \(R_1\) и \(R_2\) — сопротивление резисторов 1 и 2, \(r\) — внутреннее сопротивление источника. Тогда ЭДС равно \[\xi=I_1(R_1+r)=I_2(R_2+r)\] Выразим отсюда внутреннее сопротивление проводника \[r=\dfrac{I_2R_2-I_1R_1}{I_1-I_2}\] Также найдем ЭДС источника, для этого подставим внутреннее сопротивление в закон Ома для полной цепи для первого случая, предварительно выразив ЭДС \[\xi=I_1(R_1+\dfrac{I_2R_2-I_1R_1}{I_1-I_2})\] В третьем же случае общее сопротивление цепи равно \(R=\dfrac{R_1R_2}{R_1+R_2}\)
Тогда сила тока в третьем случае равна \[I_3=\dfrac{I_1(R_1+\dfrac{I_2R_2-I_1R_1}{I_1-I_2})}{\dfrac{R_1R_2}{R_1+R_2}+\dfrac{I_2R_2-I_1R_1}{I_1-I_2}}\] \[I_3=\dfrac{3(3+\dfrac{2 \cdot5-3\cdot 3 }{3-2})}{\dfrac{3\cdot5}{3+5}+\dfrac{2 \cdot5-3\cdot 3 }{3-2}=4,2\text{ А}}\]
При коротком замыкании клемм источника тока сила тока в цепи равна \(I_\text{кз}=12 А\). При подключении к клеммам электрической лампы электрическим сопротивлением \(R_1=5\) Ом сила тока в цепи равна \(I_1=2\) А. Определите внутреннее сопротивление источника.
Ток в замкнутой цепи определяется по закону Ома для полной цепи. \[I=\dfrac{\xi}{R+r},\] где \(\xi\) – ЭДС источника, \(r\) – внутреннее сопротивление источника. При коротком замыкании \(R=0\), а значит внутреннее сопротивление равно \[\xi=I_\text{ кз}r\] Для второго случая, когда лампа подлючена в цепь имеем \[I_1=\dfrac{\xi}{R_1+r}=\dfrac{I_\text{ кз}r}{R_1+r}=\] Выразим внутренее сопротивление \[r=\dfrac{I_1R}{I_\text{ кз}-I_1}=\dfrac{2\text{ А}\cdot 5\text{ Ом}}{12\text{ А}-2\text{ А}}=1\text{ Ом}\]


