.00 Задания 2020-21 года
Ошибка.
Попробуйте повторить позже
На острове Паабалор есть два племени, живущие охотой и собирательством.
Племена потребляют мясо и плоды
) Уравнения и графики КПВ имеют
вид:
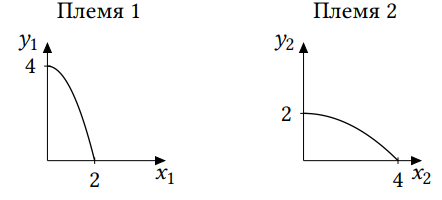
a) (8 баллов) Какое максимальное количество плодов может быть собрано на
острове, если всего нужно добыть 3 единицы мяса?
б) (8 баллов) Какое максимальное количество плодов может быть собрано на
острове, если всего нужно добыть 5 единиц мяса?
в) (14 баллов) Определите уравнение КПВ острова.
a) Найдем, как нужно разделить обязанности племен по добыче 3 единиц мяса, чтобы в итоге количество собранных плодов было максимально, то есть решим задачу
при условии , а также
. Подставляя в целевую
функцию
, получаем задачу
При этом найти максимум этой функции надо на отрезке [0;2], так как первое
племя не может добыть больше 2 единиц мяса. При этом производство второго
племени будет изменяться от 1 до 3 . Эти количества для второго племени
возможны, так что дополнительных ограничений не возникает. Находя вершину
этой параболы с ветвями вниз, получаем, что , что принадлежит отрезку
[0;2]. Значит, это и есть искомый максимум. Второе племя будет производить
единиц мяса. Общее количество собранных плодов при этом равно
.
Тот же ответ можно получить, если оптимизировать по функцию
. Оптимизировать нужно на отрезке
, так как
в силу ограничения на общее количество мяса и
, и
в силу
ограничения на общее количество мяса и
.
Кроме того, точку можно получить, приравнивая производную
целевой функции к нулю, или, что эквивалентно, приравнивая альтернативные
издержки производства для двух племен. Для первого племени альтернативные
издержки равны
, для второго
.
б) Теперь нужно решить задачу
при условиях . Аналогично пункту а),
получаем задачу
Второе племя не может добыть больше 4 единиц мяса. Значит, первому племени
надо будет добыть минимум одну единицу мяса. Таким образом, максимум этой
функции мы будем искать на отрезке [1;2]. Вершиной данной параболы с
ветвями вниз является точка , и значит, максимум будет
достигаться на краю отрезка, в точке
. Второе племя произведет все
оставшиеся четыре единицы, а количество собранных плодов будет равно
3.
Тот же ответ можно получить, если оптимизировать по функцию 6 -
. Оптимизировать нужно на отрезке
в силу
ограничения на общее количество мяса и
.
Кроме того, решение можно получить, если заметить, что производная
целевой функции
отрицательна на отрезке [1;2], или, что
эквивалентно, для любого
альтернативные издержки добычи мяса
первым племенем в точке
больше, чем альтернативные издержки добычи мяса
вторым племенем в точке
.
в) КПВ есть не что иное, как график функции, показывающей, какое
максимальное количество Игрека можно произвести, если всего требуется
произвести единиц Икса. Две точки на КПВ острова мы уже нашли - (3;5) и
(5;3). Теперь осталось найти остальные, решив ту же задачу максимизации уже
для произвольного значения
, то есть
при условиях . Ясно, что
. Переходя
к оптимизации по одной переменной, получаем задачу
где - параметр. Если
, эту задачу надо решать на отрезке
-
для любого
, второе племя сможет произвести
. Если же
, так как первое племя должно будет произвести минимум
единицы мяса.
Нетрудно определить, что вершина параболы с ветвями вниз
находится в тотiле
.
Случай 1. , и поэтому
принадлежит этому отрезку для
любого
, а значит,
будет решением задачи. Тогда
.
Случай 2. , и поэтому
.
принадлежит этому
отрезку при
, или
. Значит, решением будет
Действительно, если вершина параболы с ветвями вниз лежит левее
допустимого отрезка, оптимум достигается в левом конце отрезка. При
максимальное количество собранных плодов будет равно
Обобщая, получаем, что КПВ острова задается уравнением
Тот же ответ можно получить, оптимизируя по и обобщая анализ в пунктах
а) и б). При
максимизацию по
нужно проводить на отрезке [0;4], а при
на отрезке
. Граничное значение
определяется из
условия
.
Кроме того, решить пункт можно с помощью производной или анализа
альтернативных издержек. При является доступным распределение
, при котором производная целевой функции равна нулю
(альтернативные издержки двух племен равны). Поскольку альтернативные
издержки обоих племен возрастают, производная целевой функции убывает, и
значит, это точка максимума. При
это распределение не является
доступным, так как
. При оптимизации по
производная целевой
функции отрицательна на отрезке
альтернативные издержки первого
племени больше в точке
, чем альтернативные издержки второго племени в
точке
- и потому оптимальным является минимальное значение
, то
есть
.
а) 5
б) 3
в)
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




