Теоремы, связанными с углами (страница 2)

Из точки \(A\) на окружности проведены две прямые, пересекающие повторно окружность в точках \(B\) и \(C\), причем оказалось, что \(AC\) – диаметр, равный \(10\). Найдите длину отрезка \(AB\), если угол между этими прямыми равен \(60^\circ\).
Рассмотрим картинку:
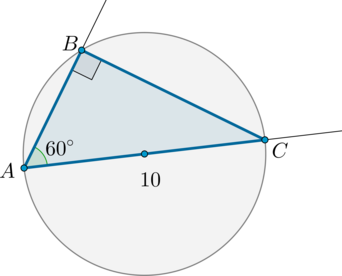
Рассмотрим \(\triangle ABC\): он прямоугольный (\(\angle B=90^\circ\), т.к. опирается на диаметр), следовательно, \(\angle C=90^\circ-\angle A=30^\circ\). Катет \(AB\), лежащий против угла \(30^\circ\), равен половине гипотенузы \(AC\), то есть равен \(5\).
На рисунке диаметр \(AB\) пересекает хорду \(PT\) и делит ее пополам, а также пересекает хорду \(KT\). Дуга \(PB\), меньшая полуокружности, равна \(75^\circ\); дуга \(AK\), меньшая полуокружности, равна \(15^\circ\).

Найдите угол между прямыми \(AB\) и \(KT\). Ответ дайте в градусах.
Рассмотрим картинку:
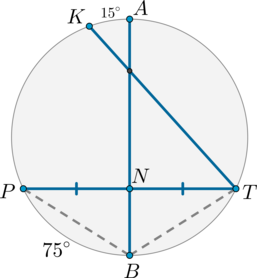
Т.к. диаметр, делящий хорду пополам, перпендикулярен ей, то \(AB\perp PT\). Следовательно, \(\triangle PNB=\triangle TNB\) как прямоугольные по двум катетам (\(PN=TN\), \(NB\) – общий). Следовательно, \(PB=TB\).
Т.к. равные хорды стягивают равные дуги, то \(\buildrel\smile\over{TB}=\buildrel\smile\over{PB}=75^\circ\).
Тогда угол между хордами \(AB\) и \(KT\) равен полусумме дуг, заключенных между ними, то есть \(0,5\left(15^\circ+75^\circ\right)=45^\circ\). Т.к. нам необходимо найти угол между прямыми (а это обязательно острый угол), то в данном случае он равен углу между данными хордами.
Касательные \(CA\) и \(CB\) к окружности образуют угол \(ACB\), равный \(112^\circ\). Найдите величину меньшей дуги \(AB\), стягиваемой точками касания. Ответ дайте в градусах.
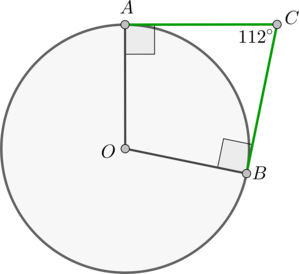
Пусть \(O\) – центр окружности. Проведем радиусы \(OA\) и \(OB\). Так как радиус, проведенный в точку касания, перпендикулярен касательной, то \(OA\perp AC, OB\perp BC\). Заметим, что \(OACB\) – четырехугольник. Так как сумма углов четырехугольника равна \(360^\circ\), то \[\angle AOB=360^\circ-112^\circ-90^\circ-90^\circ=68^\circ.\] \(\angle AOB\) – центральный угол, опирающийся на дугу \(AB\), следовательно, \(\buildrel\smile\over{AB}=\angle AOB=68^\circ\).
Хорда \(AB\) стягивает дугу окружности в \(92^\circ\). Найдите угол \(ABC\) между этой хордой и касательной к окружности, проведенной через точку \(B\). Ответ дайте в градусах.

Так как угол между хордой и касательной, проведенными из одной точки окружности, равен половине дуги, заключенной между ними, то \(\angle ABC=0,5\cdot 92^\circ=46^\circ\).
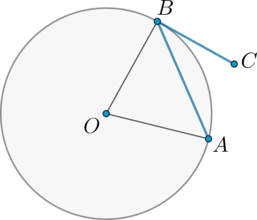
Угол между хордой \(AB\) и касательной \(BC\) к окружности равен \(32^\circ\). Найдите величину меньшей дуги, стягиваемой хордой \(AB\). Ответ дайте в градусах.
1 способ
Так как угол между хордой и касательной, проведенными из одной точки окружности, равен половине дуги, заключенной между ними, то меньшая дуга \(\buildrel\smile\over{AB}\) равна \(2\cdot 32^\circ=64^\circ\).
2 способ
Так как радиус, проведенный в точку касания, перпендикулярен касательной, то \(\angle OBC=90^\circ\). Следовательно, \(\angle OBA=90^\circ-32^\circ=58^\circ\). Так как \(OB=OA\) – радиусы, то \(\triangle OBA\) равнобедренный, следовательно, \(\angle AOB=180^\circ -2\cdot 58^\circ=64^\circ\). Так как дуга равна центральному углу, опирающемуся на нее, то меньшая дуга \(\buildrel\smile\over{AB}\) равна \(\angle AOB\) и равна \(64^\circ\).
Через концы \(A\) и \(B\) дуги окружности в \(62^\circ\) проведены касательные \(AC\) и \(BC\). Найдите угол \(ACB\). Ответ дайте в градусах.
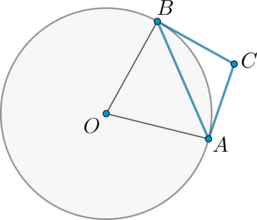
Так как угол между касательной и хордой, проведенными из одной точки окружности, равен половине дуги, заключенной между ними, то \(\angle ABC=\angle BAC=0,5\cdot 62^\circ=31^\circ\). Следовательно, из \(\triangle ABC\): \(\angle ACB=180^\circ-2\cdot 31^\circ=118^\circ\).
Угол \(ACO\) равен \(24^\circ\). Его сторона \(CA\) касается окружности с центром в точке \(O\). Найдите градусную меру дуги \(AD\), заключенной внутри этого угла, где \(B\) и \(D\) – точки пересечения секущей \(CO\) с окружностью. Ответ дайте в градусах.
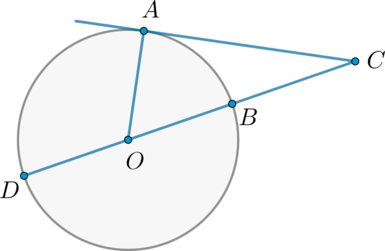
Найдем градусную меру меньшей дуги, стягиваемой хордой \(AB\). Она равна центральному углу \(AOB\), на нее опирающемуся. Так как радиус, проведенный в точку касания, перпендикулярен касательной, то \(\angle OAC=90^\circ\). Следовательно, из \(\triangle OAC\): \(\angle AOC=90^\circ-24^\circ=66^\circ\). Тогда \(\angle AOD=180^\circ-\angle AOC=114^\circ\). Дуга \(AD\), заключенная внутри угла \(ACD\), равна центральному углу \(AOD\) и равна \(114^\circ\).



