Нахождение угла между прямой и плоскостью

\(\blacktriangleright\) Угол между прямой и плоскостью – это угол между прямой и ее проекцией на эту плоскость (т.е. это угол \(0\leqslant \alpha\leqslant 90^\circ\)).
\(\blacktriangleright\) Чтобы найти угол между прямой \(a\) и плоскостью \(\phi\) (\(a\cap\phi=B\)), нужно:
Шаг 1: из какой-то точки \(A\in a\) провести перпендикуляр \(AO\) на плоскость \(\phi\) (\(O\) – основание перпендикуляра);
Шаг 2: тогда \(BO\) – проекция наклонной \(AB\) на плоскость \(\phi\);
Шаг 3: тогда угол между прямой \(a\) и плоскостью \(\phi\) равен \(\angle
ABO\).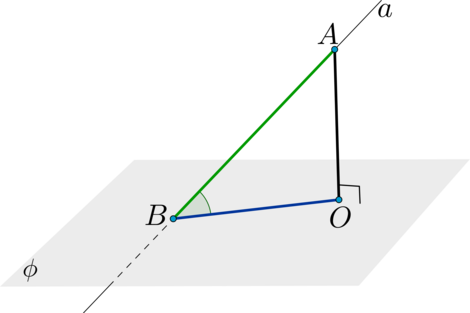
Прямая \(l\) пересекает плоскость \(\alpha\). На прямой \(l\) отмечен отрезок \(AB=25\), причем известно, что проекция этого отрезка на плоскость \(\alpha\) равна \(24\). Найдите синус угла между прямой \(l\) и плоскостью \(\alpha\)
Рассмотрим рисунок: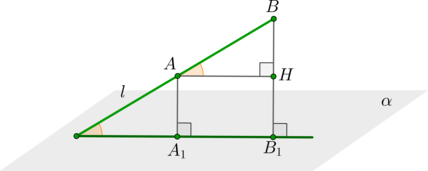
Пусть \(A_1B_1=24\) – проекция \(AB\) на плоскость \(\alpha\), значит, \(AA_1\perp \alpha\), \(BB_1\perp \alpha\). Так как две прямые, перпендикулярные к плоскости, лежат в одной плоскости, то \(A_1ABB_1\) – прямоугольная трапеция. Проведем \(AH\perp BB_1\). Тогда \(AH=A_1B_1=24\). Следовательно, по теореме Пифагора \[HB=\sqrt{AB^2-AH^2}=7.\] Заметим также, что угол между прямой и плоскостью – это угол между прямой и ее проекцией на плоскость, следовательно, искомый угол – угол между \(AB\) и \(A_1B_1\). Так как \(AH\parallel A_1B_1\), то угол между \(AB\) и \(A_1B_1\) равен углу между \(AB\) и \(AH\).
Тогда \[\sin\angle BAH=\dfrac{BH}{AB}=\dfrac7{25}=0,28.\]
\(ABC\) – правильный треугольник со стороной \(3\), \(O\) – точка, лежащая вне плоскости треугольника, причем \(OA=OB=OC=2\sqrt3\). Найдите угол, который образуют прямые \(OA, OB, OC\) с плоскостью треугольника. Ответ дайте в градусах.
Проведем перпендикуляр \(OH\) на плоскость треугольника.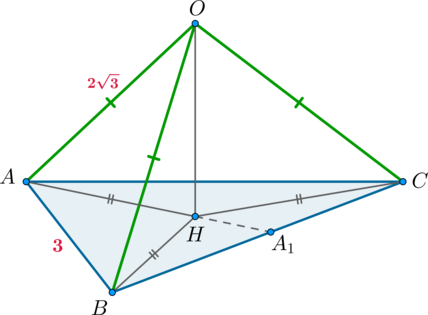
Рассмотрим \(\triangle OAH, \triangle OBH, \triangle OCH\). Они являются прямоугольными и равны по катету и гипотенузе. Следовательно, \(AH=BH=CH\). Значит, \(H\) – точка, находящаяся на одинаковом расстоянии от вершин треугольника \(ABC\). Следовательно, \(H\) – центр описанной около него окружности. Так как \(\triangle
ABC\) – правильный, то \(H\) – точка пересечения медиан (они же высоты и биссектрисы).
Так как угол между прямой и плоскостью – это угол между прямой и ее проекцией на эту плоскость, а \(AH\) – проекция \(AO\) на плоскость треугольника, то угол между \(AO\) и плоскостью треугольника равен \(\angle OAH\).
Пусть \(AA_1\) – медиана в \(\triangle ABC\), следовательно, \[AA_1=\sqrt{AB^2-BA_1^2}=\dfrac{3\sqrt3}2.\] Так как медианы точкой пересечения делятся в отношении \(2:1\), считая от вершины, то \[AH=\dfrac23AA_1=\sqrt3.\] Тогда из прямоугольного \(\triangle OAH\):\[\cos
OAH=\dfrac{AH}{AO}=\dfrac12\quad\Rightarrow\quad \angle
OAH=60^\circ.\]
Заметим, что из равенства треугольников \(OAH, OBH, OCH\) следует, что \(\angle OAH=\angle OBH=\angle OCH=60^\circ\).
Прямая \(l\) перпендикулярна плоскости \(\pi\). Прямая \(p\) не лежит в плоскости \(\pi\) и не параллельна ей, также не параллельна прямой \(l\). Найдите сумму углов между прямыми \(p\) и \(l\) и между прямой \(p\) и плоскостью \(\pi\). Ответ дайте в градусах.
Из условия следует, что прямая \(p\) пересекает плоскостью \(\pi\). Пусть \(p\cap l=O\), \(l\cap \pi=L\), \(p\cap\pi=P\).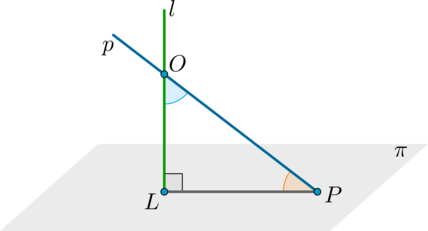
Тогда \(\angle POL\) – угол между прямыми \(p\) и \(l\).
Так как угол между прямой и плоскостью – угол между прямой и ее проекцией на эту плоскость, то \(\angle OPL\) – угол между \(p\) и \(\pi\). Заметим, что \(\triangle OPL\) прямоугольный с \(\angle
L=90^\circ\). Так как сумма острых углов прямоугольного треугольника равна \(90^\circ\), то \(\angle POL+\angle OPL=90^\circ\).
Замечание.
Если прямая \(p\) не пересекает прямую \(l\), то проведем прямую \(p'\parallel p\), пересекающую \(l\). Тогда угол между прямой \(p\) и \(l\) будет равен углу между \(p'\) и \(l\). Аналогично угол между \(p\) и \(\pi\) будет равен углу между \(p'\) и \(\pi\). А для прямой \(p'\) уже верно предыдущее решение.
\(ABCDA_1B_1C_1D_1\) – куб. Точка \(N\) – середина ребра \(BB_1\), а точка \(M\) – середина отрезка \(BD\). Найдите \(\mathrm{tg}^2\, \alpha\), где \(\alpha\) – угол между прямой, содержащей \(MN\), и плоскостью \((A_1B_1C_1D_1)\). Ответ дайте в градусах.
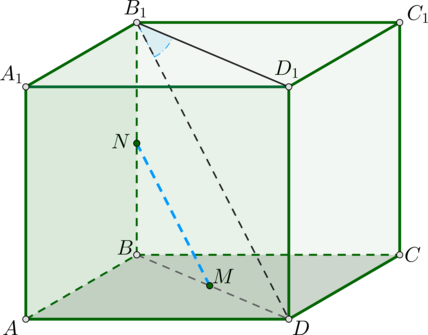
\(NM\) – средняя линия в треугольнике \(DBB_1\), тогда \(NM \parallel B_1D\) и \(\alpha\) равен углу между \(B_1D\) и плоскостью \((A_1B_1C_1D_1)\).
Так как \(DD_1\) – перпендикуляр к плоскости \(A_1B_1C_1D_1\), то \(B_1D_1\) проекция \(B_1D\) на плоскость \((A_1B_1C_1D_1)\) и угол между \(B_1D\) и плоскостью \((A_1B_1C_1D_1)\) есть угол между \(B_1D\) и \(B_1D_1\).
Пусть ребро куба \(x\), тогда по теореме Пифагора \[B_1D_1^2 = x^2 + x^2\qquad\Rightarrow\qquad B_1D_1 = x\sqrt{2}.\] В треугольнике \(B_1D_1D\) тангенс угла между \(B_1D\) и \(B_1D_1\) равен \(\mathrm{tg}\,\angle DB_1D_1=\dfrac{DD_1}{B_1D_1} = \dfrac{1}{\sqrt{2}}=\mathrm{tg}\,\alpha\), откуда \(\mathrm{tg}^2\, \alpha = \dfrac{1}{2}\).
\(ABCDA_1B_1C_1D_1\) – куб. Точка \(N\) – середина ребра \(BB_1\), а точка \(M\) делит отрезок \(BD\) в отношении \(1:2\), считая от вершины \(B\). Найдите \(9\mathrm{ctg}^2\, \alpha\), где \(\alpha\) – угол между прямой, содержащей \(MN\), и плоскостью \((ABC)\). Ответ дайте в градусах.
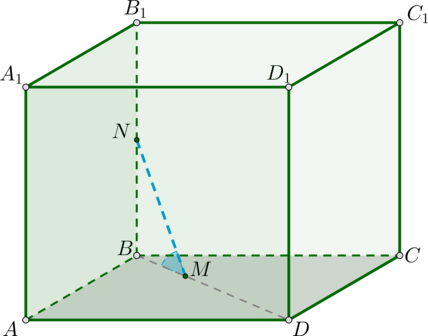
Так как \(NB\) – часть \(BB_1\), а \(BB_1\perp (ABC)\), то и \(NB\perp (ABC)\). Следовательно, \(BM\) – проекция \(NM\) на плоскость \((ABC)\). Значит, угол \(\alpha\) равен \(\angle NMB\).
Пусть ребро куба равно \(x\). Тогда \(NB=0,5x\). По теореме Пифагора \(BD=\sqrt{x^2+x^2}=\sqrt2x\). Так как по условию \(BM:MD=1:2\), то \(BM=\frac13BD\), следовательно, \(BM=\frac{\sqrt2}3x\).
Тогда из прямоугольного \(\triangle NBM\): \[\mathrm{ctg}\,\alpha=\mathrm{ctg}\,\angle NMB=\dfrac{BM}{NB}=\dfrac{2\sqrt2}3 \quad\Rightarrow\quad 9\mathrm{ctg}^2\,\alpha=8.\]
Чему равен \(\mathrm{ctg^2}\,\alpha\), если \(\alpha\) – угол наклона диагонали куба к одной из его граней?
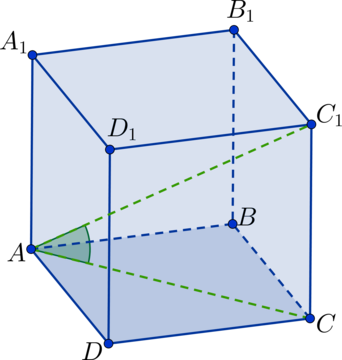
Искомый угол будет совпадать с углом между диагональю куба и диагональю любой его грани, т.к. в данном случае диагональ куба будет являться наклонной, диагональ грани – проекцией этой наклонной на плоскость грани. Таким образом, искомый угол будет равен, например, углу \(C_1AC\). Eсли обозначить ребро куба за \(x\), то \(AC=\sqrt{x^2+x^2}=\sqrt2 x\), тогда квадрат котангенса искомого угла: \[\mathrm{ctg^2}\,\alpha =(AC:CC_1)^2= (\sqrt2 x:x)^2 = 2.\]
Дан треугольник \(ABC\) с углом \(\angle A=60^\circ\). Вне плоскости треугольника отмечена точка \(O\) такая, что \(OB=OC\) и \(OB\perp AB\), \(OC\perp AC\). Известно, что \(OB=\sqrt{22}\), \(OA=5\). Найдите косинус угла между прямой \(OA\) и плоскостью треугольника.
Проведем \(OH\perp(ABC)\).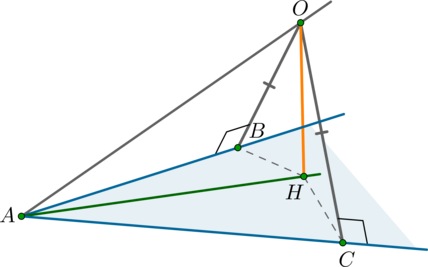
Тогда \(AH\) – проекция прямой \(OA\) на плоскость \(ABC\) и необходимо найти косинус угла \(\angle OAH\).
Заметим, что \(\triangle OAB=\triangle OAC\) как прямоугольные по катету и гипотенузе. Следовательно, \(AB=AC\). Следовательно, \(\triangle ABH=\triangle ACH\) также как прямоугольные по катету и гипотенузе. Значит, \(\angle BAH=\angle CAH=30^\circ\).
По теореме Пифагора \[AB=\sqrt{AO^2-OB^2}=\sqrt3.\] Следовательно, \[\cos 30^\circ=\dfrac{AB}{AH}\quad\Rightarrow\quad AH=\dfrac{AB}{\cos 30^\circ}=2.\] Так как \(OH\perp (ABC)\), то \(OH\) перпендикулярно любой прямой из этой плоскости, значит, \(\triangle OAH\) – прямоугольный. Тогда \[\cos \angle OAH=\dfrac{AH}{AO}=\dfrac25=0,4.\]
Учащимся старших классов на этапе подготовки к ЕГЭ по математике будет полезно научиться справляться с заданиями из раздела «Геометрия в пространстве», в которых требуется найти угол между прямой и плоскостью. Опыт прошлых лет показывает, что подобные задачи вызывают у выпускников определенные сложности. При этом знать базовую теорию и понимать, как найти угол между прямой и плоскостью, должны старшеклассники с любым уровнем подготовки. Только в этом случае они смогут рассчитывать на получение достойных баллов.
Основные нюансы
Как и другие стереометрические задачи ЕГЭ, задания, в которых требуется найти углы и расстояния между прямыми и плоскостями, могут быть решены двумя методами: геометрическим и алгебраическим. Учащиеся могут выбрать наиболее удобный для себя вариант. Согласно геометрическому методу, необходимо найти на прямой подходящую точку, опустить из нее перпендикуляр на плоскость и построить проекцию. После этого выпускнику останется применить базовые теоретические знания и решить планиметрическую задачу на вычисление угла. Алгебраический метод предполагает введение системы координат для нахождения искомой величины. Необходимо определить координаты двух точек на прямой, правильно составить уравнение плоскости и решить его.
Эффективная подготовка вместе со «Школково»
Чтобы занятия проходили легко и даже сложные задания не вызывали затруднений, выбирайте наш образовательный портал. Здесь представлен весь необходимый материал для успешной сдачи аттестационного испытания. Нужную базовую информацию вы найдете в разделе «Теоретическая справка». А для того чтобы попрактиковаться в выполнении заданий, достаточно перейти в «Каталог» на нашем математическом портале. В этом разделе собрана большая подборка упражнений разной степени сложности. В «Каталоге» регулярно появляются новые задания.
Выполнять задачи на нахождение угла между прямой и плоскостью или на нахождение угла между прямыми, российские школьники могут в режиме онлайн, находясь в Москве или другом городе. По желанию учащегося любое упражнение можно сохранить в «Избранное». Это позволит при необходимости быстро его найти и обсудить ход его решения с преподавателем.



