Задачи на нахождение площади и периметра треугольника (страница 3)

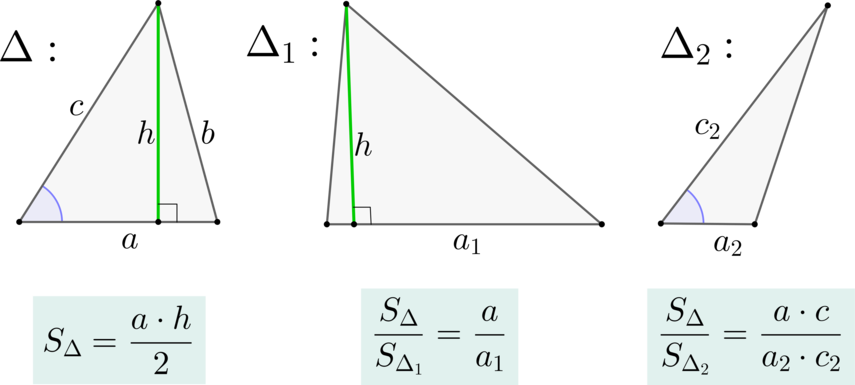
\(\blacktriangleright\) Площадь треугольника равна полупроизведению основания \(a\) и высоты \(h\), проведенной к этому основанию.
\(\blacktriangleright\) Формула Герона для площади треугольника:
\(\large{S_{\triangle}=\sqrt{p(p-a)(p-b)(p-c)}}\), где \(p\) – полупериметр.
\(\blacktriangleright\) Если треугольники имеют равные высоты (\(\triangle\) и \(\triangle_{1}\)), то их площади относятся как основания, к которым эти высоты проведены.
Как следствие: медиана треугольника делит его на два равновеликих (равных по площади) треугольника.
\(\blacktriangleright\) Если треугольники имеют по равному углу (\(\triangle\) и \(\triangle_{2}\)), то их площади относятся как произведения сторон, образующих этот угол.
Диагонали трапеции \(ABCD\) пересекаются в точке \(O\). \(DC\) – большее основание трапеции. Площадь треугольника \(ADO\) равна 12, \(DO = 2BO\). Найдите площадь трапеции.
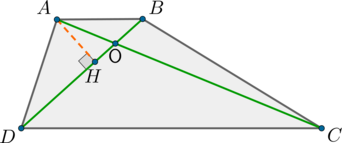
По формуле площади треугольника:
\[S_{ADO} = 0,5\cdot 2BO\cdot OH\Rightarrow S_{AOB} = 0,5\cdot BO\cdot OH =12 : 2 = 6.\]
Т.к. \(AB\parallel DC\Rightarrow \) треугольники \(AOB\) и \(DOC\) подобны и коэффициент подобия:
\[k = \dfrac{DO}{BO} = 2\Rightarrow \dfrac{S_{DOC}}{S_{AOB}}= k^2 = 4.\] \[S_{DOC} = 6\cdot 4 =24, S_{BOC} = S_{AOD} = 12.\] \[S_{ABCD} = S_{AOD} + S_{AOB} + S_{DOC} + S_{BOC} = 54.\]
В треугольнике \(ABC\) даны три стороны: \(AB=26, BC=30, AC=28\). Найдите площадь треугольника, заключенного между биссектрисой и высотой, проведенными из вершины \(B\).
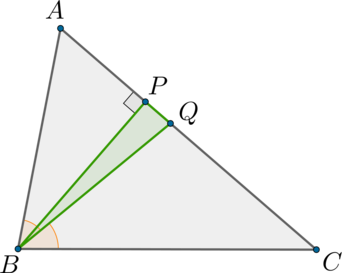
Пусть \(BP\) и \(BQ\) - высота и биссектриса данного треугольника \(ABC\) соответственно. По формуле Герона:
\[S_{ABC} = \sqrt{42\cdot(42 - 30)(42 - 28)(42 - 26)}=14\cdot6\cdot4 = 336.\]
Запишем формулу площади треугольника \(ABC\) через высоту: \(S_{ABC} = \dfrac{AC\cdot BP}2\). Тогда
\[BP = \dfrac{2\cdot S_{ABC}}{AC} = \dfrac{2\cdot 336}{28} = 24.\]
Из свойства биссектрисы треугольника: \(\dfrac{AQ}{QC} = \dfrac{AB}{BC} = \dfrac{13}{15}.\)
Поэтому: \(AQ = \dfrac{13}{28}\cdot AC =13.\)
По теореме Пифагора из прямоугольного треугольника \(APB\):
\[AP = \sqrt{AB^2-BP^2} = \sqrt{26^2-24^2} = 10.\]
Слeдовательно, \(PQ = AQ - AP = 13-10=3, S_{BPQ} = \dfrac{1}2 \cdot PQ \cdot BP = \dfrac{3\cdot 24}2 = 36.\)
В треугольнике \(ABC\) точка \(H\) делит сторону \(AB\) в отношении \(\dfrac{2}3\), считая от вершины \(B\). Найдите площадь треугольника \(HBC\), если площадь треугольника \(ABC\) равна \(15\).
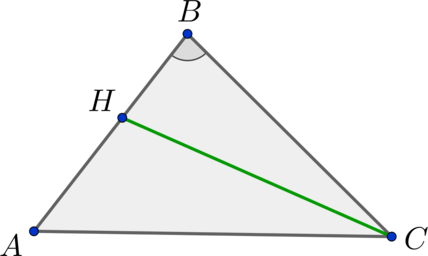
Треугольники \(ABC\) и \(HBC\) имеют общий угол \(B\), следовательно:
\[\dfrac{S_{HBC}}{S_{ABC}} = \dfrac{HB\cdot BC}{AB\cdot BC} = \dfrac{HB}{AB}.\]
Пусть \(HB = 2x\), \(AH = 3x\), учитывая то, что \(AB = HB + AH\), получаем:
\[\dfrac{HB}{AB} = \dfrac{2x}{2x+3x} = \dfrac{2}5 \quad\Rightarrow \quad S_{HBC} = S_{ABC} \cdot \dfrac{2}5 = 6.\]
В треугольнике \(ABC\) со сторонами \(BC = 6, AB = 4\) проведена биссектриса \(BD\). Высота \(DH\) треугольника \(DBC\) равна \(3\). Найдите площадь треугольника \(ABC\).
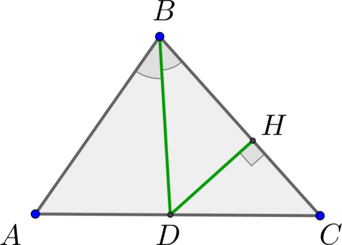
Биссектриса делит треугольник \(ABC\) на два треугольника, имеющие по равному углу, следовательно, их площади относятся как произведения сторон, образующих эти углы:
\[\dfrac{S_{ABD}}{S_{DBC}} = \dfrac{AB\cdot BD}{BC\cdot BD} = \dfrac{AB}{BC}\quad (*)\] Площадь треугольника \(BDC\) равна
\[S_{DBC} = \dfrac{1}2\cdot DH\cdot BC = \dfrac{1}2\cdot 3\cdot 6 = 9.\] Найдем площадь треугольника \(ABD\) из отношения \((*)\):
\[S_{ABD} = \dfrac{4}6\cdot S_{DBC} = \dfrac{4}6\cdot 9 = 6.\] Сложим площади треугольников \(ABD\) и \(DBC\) и получим площадь искомого треугольника \(ABC\):
\[S_{ABC} = S_{ABD} + S_{DBC} = 6 + 9 =15.\]
В прямоугольном треугольнике \(ABC\) построен отрезок \(AD\), причем \(BD = 4\), \(D\in BC\). Найдите площадь треугольника \(ABD\), если \(\angle C = 90^\circ , AC = 5\).
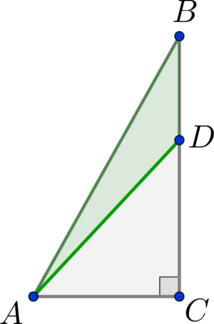
Так как \(AC\) перпендикулярна прямой \(BC\), то \(AC\) – высота тупоугольного треугольника \(ABD\), опущенная из вершины \(B\) на продолжение стороны \(BD\). Так как площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию, то \[S_{ABD}=\dfrac12\cdot BD\cdot AC=\dfrac12\cdot 4\cdot 5=10\]
В треугольнике \(KDA\) проведена медиана \(DB = 3\). Найдите площадь треугольника \(KDA\), если известно, что \(KD = 4, KA = 10\).
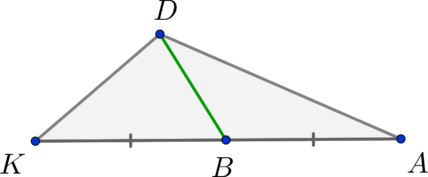
Медиана \(DB\) делит \(KA\) пополам \(\Rightarrow KB = 5\). Так как известны все стороны треугольника \(KDB\), найдем его площадь по формуле Герона: \[S_{KDB} = \sqrt{6\cdot(6 - 3)(6 - 4)(6 - 5)}=6.\] Медиана треугольника делит его на два равновеликих треугольника, то есть \(S_{KDB}=S_{ADB}\), следовательно,
\[S_{KDA} = 2\cdot S_{KDB} = 12.\]
В прямоугольном треугольнике \(ABC\) с прямым углом \(C\) проведена биссектриса \(BT\), причем \(AT = 15, TC = 12\). Найдите площадь треугольника \(ABT\).
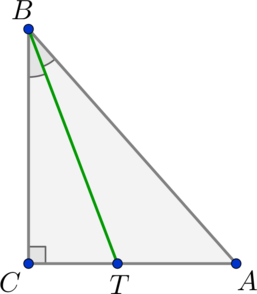
По свойству биссектрисы: \[\dfrac{TC}{BC} = \dfrac{AT}{AB}\] Пусть \(BC = x, AB = y\), тогда: \[\dfrac{12}x = \dfrac{15}y\Rightarrow x = 0,8\cdot y.\] Из треугольника \(ABC\) имеем по теореме Пифагора: \(x^2+27^2 =
y^2\Rightarrow 0,64\cdot y^2 + 27^2 = y^2\Rightarrow y = 45, x =
36.\) \[S_{ABT} = 0,5\cdot AT\cdot BC = 0,5\cdot 15\cdot 36 = 270.\]



