Треугольник: задачи на подобие (страница 2)

\(\blacktriangleright\) Треугольники подобны, если их углы равны, а сходственные стороны (лежащие напротив равных углов) относятся друг к другу с одним и тем же коэффициентом \(k\) (пропорциональны).
\(\blacktriangleright\) Признаки подобия:
1. Два угла одного треугольника равны двум углам другого треугольника.
2. Три стороны одного треугольника пропорциональны трем сторонам другого треугольника.
3. Две стороны одного треугольника пропорциональны двум сторонам другого, а углы между этими сторонами равны.
\(\blacktriangleright\) Площади подобных треугольников относятся как \(k^2\), а периметры – как \(k\).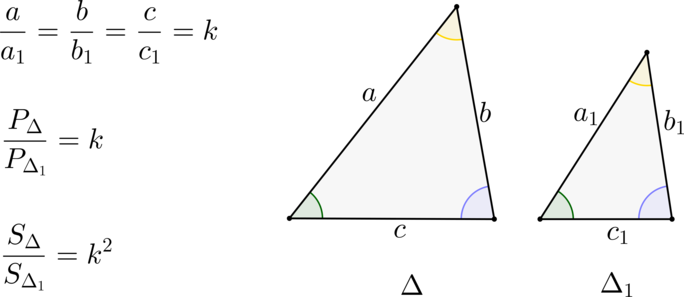
\(\blacktriangleright\) Средняя линия треугольника – отрезок, соединяющий середины двух сторон. Она равна половине третьей стороны.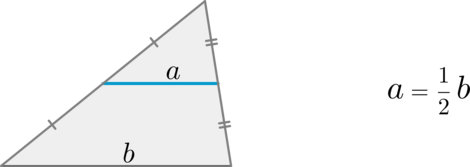
В четырёхугольнике \(ABCD\): \(BC = 5\), \(AD = 20\), \(\angle B = \angle ACD\), \(\angle D = \angle BAC\). Найдите \(AC\).
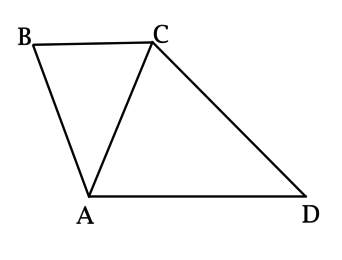
Треугольники \(ABC\) и \(ACD\) подобны по двум углам (\(\angle B = \angle ACD\), \(\angle D = \angle BAC\)).
Так как в подобных треугольниках против равных углов лежат пропорциональные стороны, то
\(\dfrac{BC}{AC} = \dfrac{AC}{AD}\). Обозначим \(AC = x\), тогда имеем \[\dfrac{5}{x} = \dfrac{x}{20},\] откуда \(x^2 = 100\), следовательно, \(x = \pm 10\), но \(x > 0\), тогда \(x = 10\).
В трапеции \(ABCD\) с основаниями \(BC = 7,5\) и \(AD = 30\) диагональ \(AC = 15\). Найдите площадь трапеции \(ABCD\), если \(S_{ABC} = 2\).
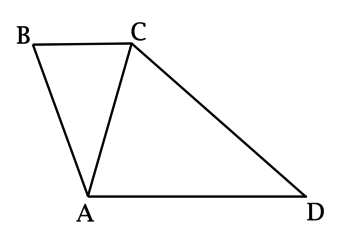
Рассмотрим треугольники \(ABC\) и \(ACD\):
\(\angle BCA = \angle CAD\),
\[\dfrac{BC}{AC} = \dfrac{1}{2} = \dfrac{AC}{AD},\] тогда треугольники \(ABC\) и \(ACD\) подобны по пропорциональности двух сторон и равенству углов между ними, следовательно, их площади относятся как квадрат коэффициента подобия: \[\dfrac{S_{ABC}}{S_{ACD}} = \left(\dfrac{BC}{AC}\right)^2 = \dfrac{1}{4},\] откуда \(S_{ACD} = 4\cdot S_{ABC} = 8\).
\(S_{ABCD} = S_{ABC} + S_{ACD} = 2 + 8 = 10\).
Точка \(D\) лежит на стороне \(BC\) треугольника \(ABC\), причём \(\dfrac{CD}{DB} = 0,2\). Точка \(E\) лежит на стороне \(AC\), причём \(\dfrac{CE}{CA} = \dfrac{1}{6}\). Найдите \(\dfrac{S_{ABF}}{S_{EFD}}\), если \(F\) – точка пересечения \(AD\) и \(BE\).
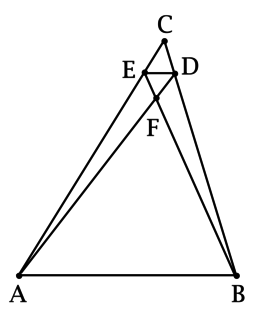
Рассмотрим треугольники \(ABC\) и \(EDC\): \(\angle C\) – общий; \(\dfrac{CE}{CA} = \dfrac{1}{6}\); так как \(\dfrac{CD}{DB} = 0,2\), то \(DB = 5 CD\) и, значит, \(\dfrac{CD}{CB} = \dfrac{1}{6} = \dfrac{CE}{CA}\), тогда треугольники \(ABC\) и \(EDC\) подобны по пропорциональности двух сторон и равенству углов между ними, следовательно, \(\dfrac{ED}{AB} = \dfrac{1}{6}\) и \(\angle CED = \angle CAB\).
Из равенства соответственных углов при параллельных прямых и секущей (\(\angle CED = \angle CAB\)) следует, что \(ED\parallel AB\), откуда можно сделать вывод: \(\angle DEF = \angle ABF\) (как внутренние накрест лежащие при параллельных прямых и секущей).
Кроме того, \(\angle EFD = \angle AFB\) как вертикальные, тогда треугольники \(ABF\) и \(DEF\) подобны (по двум углам).
Так как \(\dfrac{ED}{AB} = \dfrac{1}{6}\), то \(\dfrac{AB}{ED} = 6\), то есть коэффициент подобия треугольников \(ABF\) и \(DEF\) равен \(6\). Площади подобных треугольников относятся как квадрат коэффициента подобия, тогда \[\dfrac{S_{ABF}}{S_{EFD}} = 6^2 = 36.\]
В треугольнике \(ABC\): \(CM\) – медиана, точка \(N\) лежит на \(CM\) так, что \(\dfrac{CN}{CM} = 0,25\), \(AK\) проходит через точку \(N\), причём точка \(K\) лежит на \(BC\). Найдите \(\dfrac{KB}{CK}\).
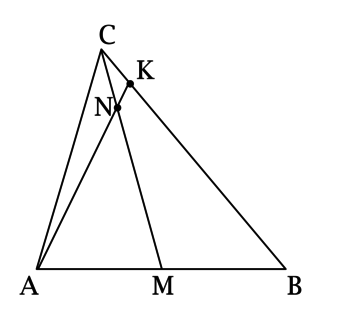
Построим \(MP \parallel AK\):
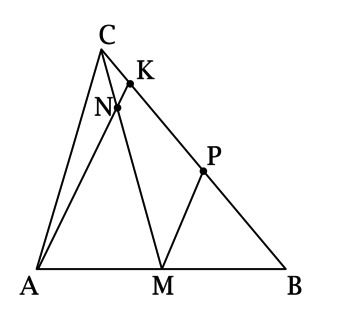
Обозначим \(KP = x\), \(CK = y\). \(MP\) – средняя линия в треугольнике \(ABK\), тогда \(BP = x\).
Треугольники \(CKN\) и \(CPM\) – подобны по двум углам (\(\angle MCP\) – общий, \(\angle CNK = \angle CMP\), как соответственные при параллельных прямых и секущей), тогда
\(\dfrac{CN}{CM} = \dfrac{CK}{CP}\), то есть \(0,25 = \dfrac{y}{y + x}\), откуда \(4 = \dfrac{y + x}{y}\), то есть \(\dfrac{x}{y} = 3\). \(KB = 2x\), тогда \[\dfrac{KB}{CK} = \dfrac{2x}{y} = 2\cdot\dfrac{x}{y} = 2\cdot 3 = 6.\]
Миша решает задачу по геометрии. У него получилось, что треугольник \(T_1\) подобен треугольнику \(T_2\), причём коэффициент подобия этих треугольников \(k_{1,2} = 4\). Кроме того, треугольник \(T_1\) оказался подобен треугольнику \(T_3\), причём коэффициент подобия этих треугольников \(k_{1,3} = 8\). Известно, что периметр треугольника \(T_1\) больше, чем периметр любого из треугольников \(T_2\) и \(T_3\). Во сколько раз площадь треугольника \(T_1\) больше, чем сумма площадей треугольников \(T_2\) и \(T_3\)?
Отношение периметров подобных треугольников равно коэффициенту их подобия, тогда \[\dfrac{P_{T_1}}{P_{T_2}} = 4,\qquad\qquad \dfrac{P_{T_1}}{P_{T_3}} = 8\,.\]
Отношение площадей подобных треугольников равно квадрату коэффициента их подобия, тогда \[\dfrac{S_{T_1}}{S_{T_2}} = 4^2 = 16,\qquad\qquad \dfrac{S_{T_1}}{S_{T_3}} = 8^2 = 64\,,\] откуда получаем \[S_{T_2} = \dfrac{S_{T_1}}{16},\qquad\qquad S_{T_3} = \dfrac{S_{T_1}}{64}\,,\] следовательно, \[\dfrac{S_{T_1}}{S_{T_2} + S_{T_3}} = S_{T_1} : \left(\dfrac{S_{T_1}}{16} + \dfrac{S_{T_1}}{64}\right) = \dfrac{64}{5} = 12,8\]
Точка \(D\) лежит на стороне \(AB\) треугольника \(ABC\), причём \(\dfrac{AD}{DB} = 0,5\). Точка \(E\) лежит на \(CD\), причём \(\dfrac{CE}{ED} = 0,5\). Точка \(F\) лежит на пересечении прямых, содержащих отрезки \(AC\) и \(BE\). Найдите \(\dfrac{AF}{FC}\).
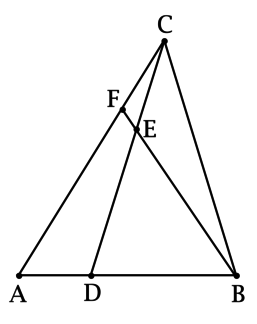
Построим \(DG \parallel BF\):
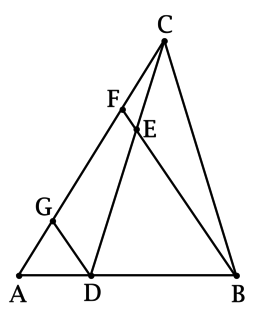
Обозначим \(AG = x\), \(FC = y\).
Рассмотрим треугольники \(ADG\) и \(ABF\): \(\angle A\) – общий, \(\angle AGD = \angle AFB\) (как соответственные при параллельных прямых и секущей), тогда треугольники \(ADG\) и \(ABF\) подобны по двум углам и \[\dfrac{AG}{AF} = \dfrac{AD}{AB}.\] Так как \(\dfrac{AD}{DB} = 0,5\), то \(DB = 2\cdot AD\), тогда \(AB = 3\cdot AD\) и \(\dfrac{1}{3} = \dfrac{AD}{AB} = \dfrac{AG}{AF}\), тогда \(AF = 3x\), следовательно, \[FG = 2x.\]
Аналогично можно сделать выводы о том, что:
Треугольники \(CEF\) и \(CDG\) подобны по двум углам, тогда \(\dfrac{CF}{CG} = \dfrac{CE}{CD} = \dfrac{1}{3}\), тогда \(\dfrac{y}{y + 2x} = \dfrac{1}{3}\), откуда
\(\dfrac{y + 2x}{y} = 3\), то есть \(\dfrac{2x}{y} = 2\), следовательно, \(3 = \dfrac{3x}{y} = \dfrac{AF}{FC}\).


