Окружность: важные теоремы, связанные с длинами отрезков (страница 3)

\(\blacktriangleright\) Если радиус перпендикулярен хорде, то он делит ее пополам;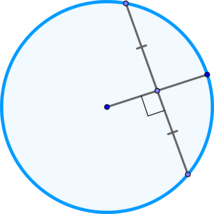
\(\blacktriangleright\) Если вписанный угол – прямой, то он опирается на диаметр;
\(\blacktriangleright\) Произведения отрезков хорд равны; \[\large{AO
\cdot OC=BO\cdot OD}\]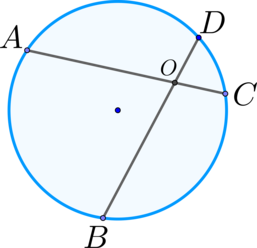
\(\blacktriangleright\) Квадрат касательной равен произведению секущей на ее внешнюю часть; \[\large{OA^2=OB\cdot OC}\]
\(\blacktriangleright\) Произведения двух секущих, проведенных из одной точки вне окружности, на их внешние части одинаковы;\[\large{
OA\cdot OC=OB\cdot OD}\]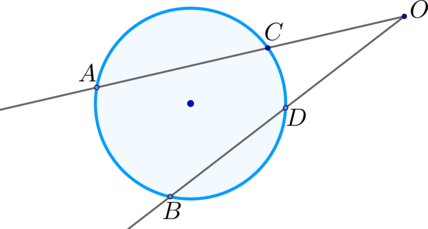
\(\blacktriangleright\) Отрезки касательных, проведенных из одной точки, равны;\[\large{OA=OB}\]
\(\blacktriangleright\) Если хорды отсекают от окружности равные дуги (меньшие полуокружности), то такие хорды равны.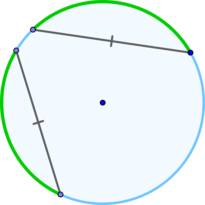
В треугольнике \(ABC\) известно, что \(AB = 2BC\), \(\angle BAC = 30^\circ\). Найдите \(\dfrac{AC^2}{BC^2}\). Если задача допускает несколько ответов – запишите полусумму наименьшего и наибольшего из них.
В прямоугольном треугольнике катет, лежащий против угла в \(30^\circ\), равен половине гипотенузы. В данном случае известно, что в треугольнике \(ABC\) сторона, лежащая против угла в \(30^\circ\), равна половине другой стороны. Значит ли это, что треугольник \(ABC\) обязательно прямоугольный? Подобного рода умозаключения в общем случае очень опасны, так как часто попросту неверны.
Но в данном конкретном случае нам повезло: докажем, что треугольник \(ABC\) – прямоугольный. В самом деле, если опустить перпендикуляр \(BH\) из точки \(B\) на прямую, содержащую \(AC\), то окажется, что \(BH = 0,5AB = BC\).
Но если при этом \(BH\) и \(BC\) не совпадают, то \(HBC\) – прямоугольный треугольник, у которого гипотенуза \(BC\) равна катету \(BH\), чего быть не может, следовательно, \(BH\) и \(BC\) совпадают и треугольник \(ABC\) – прямоугольный.
По теореме Пифагора в треугольнике \(ABC\): \[AB^2 = BC^2 + AC^2\quad\Leftrightarrow\quad 4BC^2 = BC^2 + AC^2\quad\Leftrightarrow\quad AC^2 = 3BC^2\quad\Leftrightarrow\quad \dfrac{AC^2}{BC^2} = 3\,.\]

