Геометрия на плоскости (планиметрия). Часть II (страница 3)

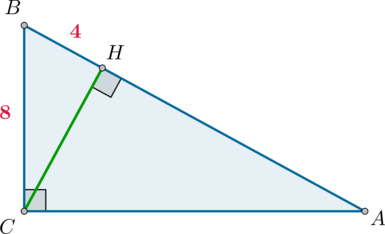
Из \(\triangle BCH\): \[\sin\angle BCH=\dfrac{BH}{BC}=0,5\] По свойству прямоугольного треугольника \(\angle BCH=\angle BAC\), следовательно, \(\sin\angle A=\sin\angle BAC=0,5\).

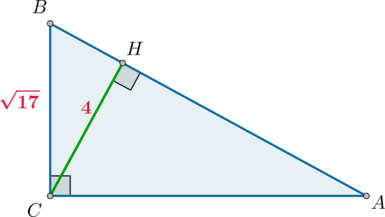
По теореме Пифагора из \(\triangle BCH\): \[BH=\sqrt{17-16}=1\] Следовательно, \[\mathrm{tg}\,\angle BCH=\dfrac{BH}{CH}=0,25\] По свойству прямоугольного треугольника \(\angle BCH=\angle BAC\), следовательно, \(\mathrm{tg}\,\angle A=\mathrm{tg}\,\angle BAC=0,25\).

Проведем высоты \(BK\) и \(DH\). Тогда из \(\triangle ADH\) и \(\triangle ABK\): \[\sin\angle A=\dfrac{DH}{AD}\quad {\small{и}}\quad \sin\angle A=\dfrac{BK}{AB}\] откуда \[DH=AD\sin\angle A\quad {\small{и}}\quad BK=AB\sin\angle A\] Так как \(AD>AB\), то \(DH\) – большая высота, следовательно, \[DH=21\cdot \dfrac67=18\]

Рассмотрим рисунок:

Проведем \(BH\perp AD\). По свойству равнобедренной трапеции \(AH=\frac12\left(AD-BC\right)=7\). Тогда по теореме Пифагора из \(\triangle ABH\): \[BH=\sqrt{25^2-7^2}=\sqrt{(25-7)(25+7)}=\sqrt{18\cdot 32}=3\cdot 8=24\] Тогда из \(\triangle ABH\) \[\sin\angle A=\dfrac{BH}{AB}=\dfrac{24}{25}=0,96\]

Проведем \(BH\perp AD\). По свойству равнобедренной трапеции \(AH=\frac12\left(AD-BC\right)=15\). Тогда из \(\triangle ABH\): \[\dfrac57=\cos\angle A=\dfrac{AH}{AB}\quad\Rightarrow\quad AB=21\]

Так как по определению \[\sin \angle A=\dfrac{BC}{AB}\] то нужно найти \(AB\). По теореме Пифагора \(AB=\sqrt{24^2+7^2}=\sqrt{625}=25\), следовательно, \[\sin \angle A=\dfrac{7}{25}=0,28\]

По определению синуса и косинуса: \[\sin \angle Y=\dfrac{ES}{YE} \qquad \text{и} \qquad \cos \angle E=\dfrac{ES}{YE}\]

Таким образом мы видим, что \(\cos \angle E=\sin \angle Y=0,8.\)