Вычисление синуса, косинуса и тангенса угла треугольника (страница 2)

В прямоугольном треугольнике:
\(\blacktriangleright\) Синус острого угла равен отношению противолежащего катета к гипотенузе: \[{\large{\sin \alpha = \dfrac{a}{c}}}\]
\(\blacktriangleright\) Косинус острого угла равен отношению прилежащего катета к гипотенузе: \[{\large{\cos \alpha = \dfrac{b}{c}}}\]
\(\blacktriangleright\) Тангенс острого угла равен отношению противолежащего катета к прилежащему: \[{\large{\mathrm{tg}\, \alpha = \dfrac{a}{b}}}\]
\(\blacktriangleright\) Котангенс острого угла равен отношению прилежащего катета к противолежащему: \[{\large{\mathrm{ctg}\,
\alpha =\dfrac{b}{a}}}\]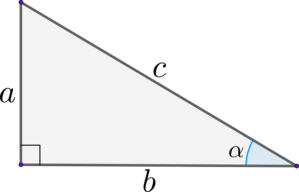
Важные формулы:
\[{\large{\begin{array}{|lcl|} \hline \sin^2 \alpha+\cos^2 \alpha
=1&\qquad& \mathrm{tg}\, \alpha \cdot \mathrm{ctg}\, \alpha
=1\\ &&\\
\mathrm{tg}\, \alpha=\dfrac{\sin \alpha}{\cos
\alpha}&&\mathrm{ctg}\, \alpha
=\dfrac{\cos \alpha}{\sin \alpha}\\&&\\
\hline
\end{array}}}\]
\[\begin{array}{|c|c|c|c|c|c|} \hline & \phantom{000}\, 0^\circ \phantom{000}& \phantom{000}\, 30^\circ \phantom{000} & \phantom{000}\, 45^\circ \phantom{000} & \phantom{000}\, 60^\circ \phantom{000} & \phantom{000}\, 90^\circ \phantom{000}\\[1ex] \hline \sin & 0 &\frac12&\frac{\sqrt2}2&\frac{\sqrt3}2 & 1\\[1ex] \hline \cos & 1 & \frac{\sqrt3}2&\frac{\sqrt2}2&\frac12 & 0\\[1ex] \hline \mathrm{tg} & 0 & \frac{\sqrt3}3&1&\sqrt3 & \text{не сущ.}\\[1ex] \hline \mathrm{ctg}& \text{не сущ.} &\sqrt3&1&\frac{\sqrt3}3 & 0\\[1ex] \hline \end{array}\]
В треугольнике \(ABC\) угол \(C=90^\circ\), \(CH\) – высота, \(BC=3\), \(\sin\angle A=\dfrac16\). Найдите \(AH\).
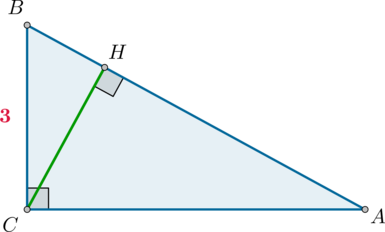
По определению из \(\triangle ABC\): \[\dfrac{BC}{AB}=\sin \angle A=\dfrac16\quad\Rightarrow\quad AB=6BC=18\] Так как по свойству прямоугольного треугольника \(\triangle AHC\sim \triangle ABC\), то \[\dfrac{AH}{AC}=\dfrac{AC}{AB}\quad\Rightarrow\quad AH=\dfrac{AC^2}{AB}\] Нужно найти \(AC^2\). По теореме Пифагора \(AC^2=AB^2-BC^2=18^2-3^2=(18-3)(18+3)=15\cdot 21\). Следовательно, \[AH=\dfrac{15\cdot 21}{18}=\dfrac{35}2=17,5\]
В треугольнике \(ABC\) угол \(C=90^\circ\), \(CH\) – высота, \(AC=2\), \(\cos\angle A=\dfrac18\). Найдите \(BH\).
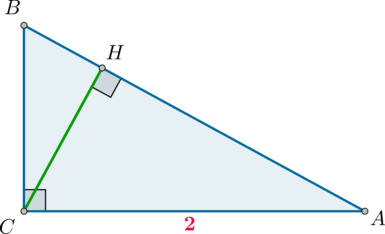
По определению из \(\triangle ABC\): \[\dfrac{AC}{AB}=\cos \angle A=\dfrac18\quad\Rightarrow\quad AB=8AC=16\] Так как по свойству прямоугольного треугольника \(\triangle BHC\sim \triangle ABC\), то \[\dfrac{BH}{BC}=\dfrac{BC}{AB}\quad\Rightarrow\quad BH=\dfrac{BC^2}{AB}\] Нужно найти \(BC^2\). По теореме Пифагора \(BC^2=AB^2-AC^2=16^2-2^2=(16-2)(16+2)=14\cdot 18\). Следовательно, \[BH=\dfrac{14\cdot 18}{16}=15,75\]
В треугольнике \(ABC\) известно, что \(AC=BC=5\), \(\sin\angle A=\dfrac{7}{25}\). Найдите \(AB\).
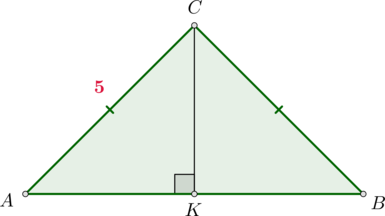
Проведем \(CK\perp AB\). Так как треугольник \(ABC\) равнобедренный, то \(CK\) также является медианой, следовательно, \(AK=0,5AB\). Тогда \[\dfrac7{25}=\sin\angle A=\dfrac{CK}{AC}\quad\Rightarrow\quad CK=\dfrac75\] Тогда по теореме Пифагора из \(\triangle ACK\): \[AK=\sqrt{AC^2-CK^2}=\sqrt{25-\frac{49}{25}}=\sqrt{\dfrac{25^2-7^2}{25}}= \sqrt{\dfrac{(25-7)(25+7)}{25}}=\dfrac{3\cdot 8}5=4,8\] Следовательно, \(AB=2AK=9,6\).
В треугольнике \(ABC\) известно, что \(AC=BC\), \(AB=8\), \(\mathrm{tg}\,\angle A=\dfrac{\sqrt{33}}4\). Найдите \(AC\).
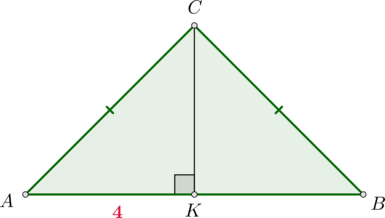
Проведем \(CK\perp AB\). Так как треугольник \(ABC\) равнобедренный, то \(CK\) также является медианой, следовательно, \(AK=0,5AB=4\). Тогда \[\dfrac{CK}{AK}=\mathrm{tg}\,\angle A=\dfrac{\sqrt{33}}4\quad\Rightarrow\quad CK=\sqrt{33}\] Тогда по теореме Пифагора из \(\triangle ACK\): \[AC=\sqrt{AK^2+CK^2}=\sqrt{16+33}=7\]
В треугольнике \(ABC\) известно, что \(AC=BC\), \(AB=8\), \(\sin\angle BAC=0,5\). Найдите высоту \(AH\).
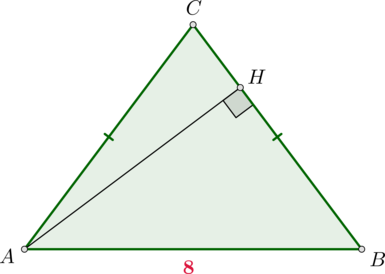
Так как \(\triangle ABC\) равнобедренный, то \(\angle BAC=\angle ABC\), следовательно, \(\sin\angle ABC=\sin\angle BAC=0,5\). Тогда из \(\triangle AHB\): \[\sin\angle ABC=\dfrac{AH}{AB}\quad\Rightarrow\quad AH=0,5AB=4\]
В треугольнике \(ABC\) известно, что \(AC=BC=4\sqrt{15}\), \(\sin\angle BAC=0,25\). Найдите высоту \(AH\).
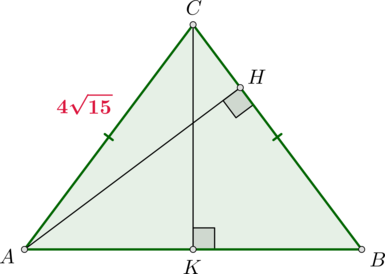
Так как \(\triangle ABC\) равнобедренный, то \(\angle BAC=\angle ABC\), следовательно, \(\sin\angle ABC=\sin\angle BAC=0,25\). Следовательно, из \(\triangle AHB\): \[\dfrac{AH}{AB}=\sin\angle ABC=\dfrac14 \quad\Rightarrow\quad AH=\dfrac14AB\] Проведем \(CK\perp AB\). Тогда \(CK\) также является медианой. Из \(\triangle CKB\): \[\dfrac{CK}{BC}=\sin\angle ABC=\dfrac14\quad\Rightarrow\quad CK=\sqrt{15}\] Следовательно, по теореме Пифагора из \(\triangle CKB\): \[KB=\sqrt{BC^2-CK^2}=\sqrt{(4\sqrt{15})^2-(\sqrt{15})^2}= \sqrt{3\sqrt{15}\cdot 5\sqrt{15}}=15\] Следовательно, \(AB=2KB=30\) и \(AH=\frac14AB=7,5\).
В треугольнике \(ABC\) известно, что \(AC=BC=27\), \(AH\) – высота, \(\cos\angle BAC=\dfrac23\). Найдите \(BH\).
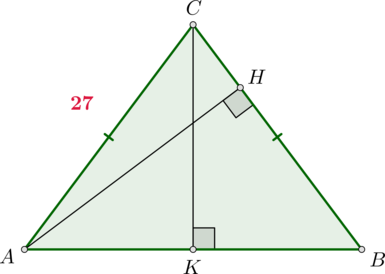
Так как \(\triangle ABC\) равнобедренный, то \(\angle BAC=\angle ABC\), следовательно, \(\cos\angle ABC=\cos\angle BAC=\frac23\).
Проведем \(CK\perp AB\). Так как \(\triangle ABC\) равнобедренный, то \(CK\) – медиана. Из \(\triangle CKB\): \[\dfrac{KB}{BC}=\cos\angle ABC=\dfrac23\quad\Rightarrow\quad KB=18\] Тогда \(AB=2KB=36\). Из \(\triangle AHB\): \[\dfrac{BH}{AB}=\cos\angle ABC=\dfrac23\quad\Rightarrow\quad
BH=24\]



