Вычисление синуса, косинуса и тангенса угла треугольника (страница 4)

В прямоугольном треугольнике:
\(\blacktriangleright\) Синус острого угла равен отношению противолежащего катета к гипотенузе: \[{\large{\sin \alpha = \dfrac{a}{c}}}\]
\(\blacktriangleright\) Косинус острого угла равен отношению прилежащего катета к гипотенузе: \[{\large{\cos \alpha = \dfrac{b}{c}}}\]
\(\blacktriangleright\) Тангенс острого угла равен отношению противолежащего катета к прилежащему: \[{\large{\mathrm{tg}\, \alpha = \dfrac{a}{b}}}\]
\(\blacktriangleright\) Котангенс острого угла равен отношению прилежащего катета к противолежащему: \[{\large{\mathrm{ctg}\,
\alpha =\dfrac{b}{a}}}\]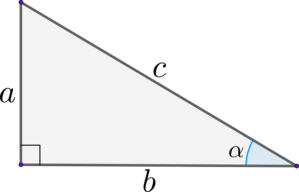
Важные формулы:
\[{\large{\begin{array}{|lcl|} \hline \sin^2 \alpha+\cos^2 \alpha
=1&\qquad& \mathrm{tg}\, \alpha \cdot \mathrm{ctg}\, \alpha
=1\\ &&\\
\mathrm{tg}\, \alpha=\dfrac{\sin \alpha}{\cos
\alpha}&&\mathrm{ctg}\, \alpha
=\dfrac{\cos \alpha}{\sin \alpha}\\&&\\
\hline
\end{array}}}\]
\[\begin{array}{|c|c|c|c|c|c|} \hline & \phantom{000}\, 0^\circ \phantom{000}& \phantom{000}\, 30^\circ \phantom{000} & \phantom{000}\, 45^\circ \phantom{000} & \phantom{000}\, 60^\circ \phantom{000} & \phantom{000}\, 90^\circ \phantom{000}\\[1ex] \hline \sin & 0 &\frac12&\frac{\sqrt2}2&\frac{\sqrt3}2 & 1\\[1ex] \hline \cos & 1 & \frac{\sqrt3}2&\frac{\sqrt2}2&\frac12 & 0\\[1ex] \hline \mathrm{tg} & 0 & \frac{\sqrt3}3&1&\sqrt3 & \text{не сущ.}\\[1ex] \hline \mathrm{ctg}& \text{не сущ.} &\sqrt3&1&\frac{\sqrt3}3 & 0\\[1ex] \hline \end{array}\]
Дан треугольник \(YES\), причем \(\angle S=90^\circ\). Известно, что \(\mathrm{tg}\,\angle Y=1,5\). Найдите \(\mathrm{ctg}\,\angle E\).

По определению тангенса и котангенса: \[\mathrm{tg}\,\angle Y=\dfrac{ES}{YS} \qquad \text{и} \qquad \mathrm{ctg}\,\angle E=\dfrac{ES}{YS}\]
Таким образом мы видим, что \(\mathrm{tg}\,\angle Y=\mathrm{ctg}\,\angle E=1,5.\)
Дан треугольник \(YES\), причем \(\angle S\) — прямой. Найдите синус угла \(E\), если синус угла \(Y\) равен \(\dfrac35\).

По определению синуса: \[\sin \angle E=\dfrac{YS}{YE}=\cos \angle Y\]
Т.к. \(\sin^2\alpha+\cos^2\alpha=1\) для любого угла \(\alpha\), то \(\cos^2\angle Y=1-(0,6)^2=0,64\), следовательно, \(\cos\angle Y=0,8\).
Значит и \(\sin \angle E=0,8\).
Дан треугольник \(YES\), причем \(YS\perp ES\). Найдите \(\mathrm{tg}\,\angle Y\), если \(\mathrm{tg}\,\angle E=4\).

По определению тангенса: \[\mathrm{tg}\,\angle Y=\dfrac{ES}{YS}=\mathrm{ctg}\,\angle E\]
Т.к. \(\mathrm{tg}\,\alpha\cdot \mathrm{ctg}\,\alpha=1\) для любого угла \(\alpha\), то \[\mathrm{ctg}\,\angle E=\dfrac1{\mathrm{tg}\,\angle E}=\dfrac14\]
Следовательно, \(\mathrm{tg}\,\angle Y=\frac14=0,25\).
В параллелограмме \(ABCD\): \(AB = 15\), \(\sin{\angle D} = 0,4\). Найдите длину \(h\) – высоты, опущенной из вершины \(B\) на сторону \(AD\).
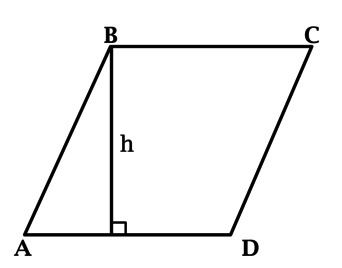
В параллелограмме сумма односторонних углов равна \(180^{\circ}\), тогда \(\sin{\angle A} = \sin{(\pi - \angle D)} = \sin{\angle D} = 0,4\).
Синус острого угла в прямоугольном треугольнике равен отношению противолежащего этому углу катета к гипотенузе, тогда \[0,4 = \dfrac{h}{AB} = \dfrac{h}{15} \qquad\Rightarrow\qquad h = 6.\]
Дан прямоугольный треугольник \(CAT\), причем \(\angle C=90^\circ\), а \(CH\) – высота этого треугольника.
Известно, что \(\sin \angle
ACH=\frac25\), \(AT=8\). Найдите \(AH\).

По определению синуса \(\sin \angle ACH=\dfrac{AH}{AC}\). Для того, чтобы найти \(AH\), необходимо найти \(AC\).
Т.к. высота прямоугольного треугольника \(CAT\), опущенная из вершины прямого угла, делит его на два треугольника, каждый из которых подобен \(\triangle CAT\), то \(\angle ACH=\angle ATC\). Значит, и \(\sin \angle ACH=\sin \angle ATC=\frac25\).
Но по определению \[\sin \angle ATC=\dfrac{AC}{AT} \quad \Rightarrow \quad \dfrac25=\dfrac{AC}8 \quad \Leftrightarrow \quad AC=\dfrac{16}5\]
Значит, \[\dfrac25=\dfrac{AH}{AC} \quad \Rightarrow \quad AH=AC\cdot \dfrac25=\dfrac{32}{25}=1,28.\]
В треугольнике \(ABC\) сторона \(AC=12\), \(\mathrm{tg}\,A=\dfrac{\sqrt2}4\). Найдите высоту \(CH\).
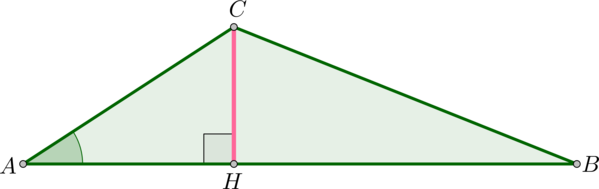
Рассмотрим прямоугольный \(\triangle ACH\). Так как тангенс – это отношение противолежащего катета к прилежащему, то \[\dfrac{CH}{AH}=\dfrac{\sqrt2}4\] Следовательно, можно принять \(CH=\sqrt2x\), \(AH=4x\), где \(x\) – некоторое положительное число. Тогда по теореме Пифагора из этого же треугольника \[AC^2=AH^2+CH^2\quad\Rightarrow\quad 144=2x^2+16x^2\quad\Rightarrow\quad x=2\sqrt2.\] Следовательно, \[CH=\sqrt2x=\sqrt2\cdot 2\sqrt2=4.\]
В ромбе \(ABCD\) одна из диагоналей в \(\sqrt{3}\) раз больше, чем другая диагональ. Найдите больший из углов этого ромба. Ответ дайте в градусах.
Пусть \(O\) – точка пересечения диагоналей ромба. Пусть \(AC : BD = \sqrt{3}\).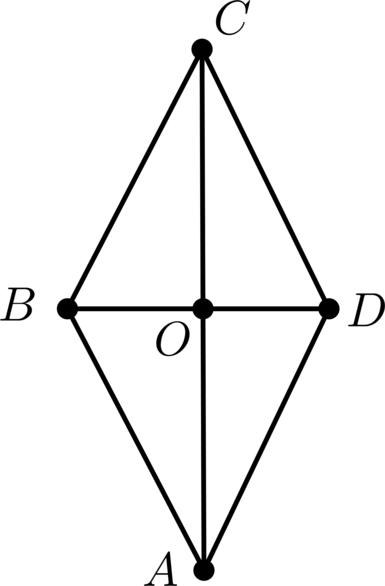
Так как \(AO = 0,5AC\), а \(BO = 0,5BD\), то \(AO : BO = \sqrt{3}\), тогда \[\mathrm{tg}\, \angle ABO = \sqrt{3}\,,\] следовательно, \(\angle ABO = 60^\circ\), тогда \(\angle ABC = 2\angle ABO = 120^\circ\).
\(\angle BCD = 60^\circ < \angle ABC\), таким образом, больший из углов ромба \(ABCD\) равен \(120^\circ\).



