Найти производную функции

Прямая, заданная уравнением \(y = x\), образует с положительным направлением оси \(Ox\) угол \(\alpha\). Найдите \(\mathrm{tg}\, \alpha\).
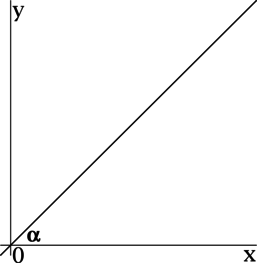
Для прямой, заданной уравнением \(y = kx + b\), коэффициент \(k\) есть значение тангенса угла между прямой \(y = kx + b\) и положительным направлением оси \(Ox\).
Так как для прямой \(y = x\) коэффициент \(k\) равен \(1\), то \(\mathrm{tg}\, \alpha = 1\).
Прямая, заданная уравнением \(y = 2x - 3\), образует с положительным направлением оси \(Ox\) угол \(\alpha\). Найдите \(\mathrm{tg}\, \alpha\).
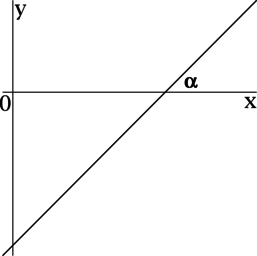
Для прямой, заданной уравнением \(y = kx + b\), коэффициент \(k\) есть значение тангенса угла между прямой \(y = kx + b\) и положительным направлением оси \(Ox\).
Так как для прямой \(y = 2x - 3\) коэффициент \(k\) равен \(2\), то \(\mathrm{tg}\, \alpha = 2\).
Прямая, заданная уравнением \(y = -x + 2\), образует с положительным направлением оси \(Ox\) угол \(\alpha\). Найдите \(\mathrm{tg}\, \alpha\).
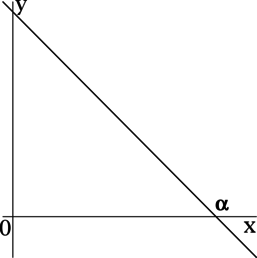
Для прямой, заданной уравнением \(y = kx + b\), коэффициент \(k\) есть значение тангенса угла между прямой \(y = kx + b\) и положительным направлением оси \(Ox\).
Так как для прямой \(y = -x + 2\) коэффициент \(k\) равен \(-1\), то \(\mathrm{tg}\, \alpha = -1\).
Прямая, заданная уравнением \(y = kx + 77\), образует с положительным направлением оси \(Ox\) угол \(\alpha\). Найдите \(k\), если \(\mathrm{tg}\, \alpha = 12\).
Для прямой, заданной уравнением \(y = kx + b\), коэффициент \(k\) есть значение тангенса угла между прямой \(y = kx + b\) и положительным направлением оси \(Ox\).
Так как тангенс угла \(\alpha\) между прямой \(y = kx + 77\) и положительным направлением оси \(Ox\) равен \(12\), то \(k = \mathrm{tg}\, \alpha = 12\).
Прямая, заданная уравнением \(y = kx + 0,2\), образует с положительным направлением оси \(Ox\) угол \(\alpha\). Найдите \(k\), если \(\mathrm{tg}\, \alpha = -3,3\).
Для прямой, заданной уравнением \(y = kx + b\), коэффициент \(k\) есть значение тангенса угла между прямой \(y = kx + b\) и положительным направлением оси \(Ox\).
Так как тангенс угла \(\alpha\) между прямой \(y = kx + 0,2\) и положительным направлением оси \(Ox\) равен \(-3,3\), то \(k = \mathrm{tg}\, \alpha = -3,3\).
Прямая, заданная уравнением \(y = kx\), образует с положительным направлением оси \(Ox\) угол \(\alpha\). Найдите \(k\), если \(\mathrm{tg}\, \alpha = 0\).
Для прямой, заданной уравнением \(y = kx + b\), коэффициент \(k\) есть значение тангенса угла между прямой \(y = kx + b\) и положительным направлением оси \(Ox\).
Так как тангенс угла \(\alpha\) между прямой \(y = kx\) и положительным направлением оси \(Ox\) равен \(0\), то \(k = \mathrm{tg}\, \alpha = 0\).
Прямая \(y = kx - 2016\) образует угол \(45^{\circ}\) с положительным направлением оси \(Ox\). Найдите \(k\).
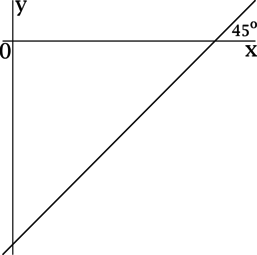
Для прямой, заданной уравнением \(y = kx + b\), коэффициент \(k\) есть значение тангенса угла между прямой \(y = kx + b\) и положительным направлением оси \(Ox\).
Так как угол между прямой \(y = kx - 2016\) и положительным направлением оси \(Ox\) равен \(\dfrac{\pi}{4}\), то \(k = \mathrm{tg}\, \dfrac{\pi}{4} = 1\).
Задания по теме «Взаимосвязь функции и ее производной» являются обязательной частью ЕГЭ по математике. Как правило, эту тему учащиеся подробно изучают в 8-9 классе. Неудивительно, что при подготовке к сдаче единого государственного экзамена выпускники нуждаются в повторении основных формул из темы «Исследование функции с помощью производной». При этом такие задания включаются и в базовый, и в профильный уровень экзамена. Именно поэтому выполнять необходимые построения для того, чтобы быстро получить правильный ответ, должны уметь все старшеклассники. Понимая, что такое производная функция, чему может быть равно ее значение, и умея ее исследовать и производить правильные вычисления, учащиеся смогут рассчитывать на получение достаточно высоких баллов по итогам написания ЕГЭ.
Базовые моменты, которые необходимо усвоить
Чтобы найти производную функции в точке и успешно справляться с задачами, в которых требуется краткое или подробное решение, важно учесть несколько основных нюансов. Учащимся стоит запомнить, что:
-
В интервалах возрастания производные заданных функций имеют положительные значения.
-
Если речь идет об интервалах убывания, знак меняется на отрицательный.
-
Производная в определенной точке равняется угловому коэффициенту касательной, которая проведена к графику функции в этой же точке.
-
Значение производной в точках экстремума соответствует нулю.
Как сделать процесс подготовки к аттестационному испытанию более легким и эффективным?
Занимаясь перед экзаменом, многие старшеклассники сталкиваются с проблемой поиска полезного источника информации. Учебника в нужный момент может просто не оказаться под рукой. А поиск нужных формул, примеров их применения и построения производной функции порой бывает достаточно трудоемким, даже в Интернете в онлайн-режиме.
Образовательный математический портал «Школково» предлагает придерживаться нового подхода к подготовке к единому государственному экзамену. Занимаясь на нашем сайте, старшеклассники смогут определить наиболее сложные для себя темы и ликвидировать пробелы в знаниях.
Чтобы задания по теме «Связь функции и производной» не вызывали затруднений, мы рекомендуем начать подготовку не с разбора примеров их решения и нахождения нужного значения на заданном промежутке, а с повторения базовой теоретической информации. Этот материал вы найдете в соответствующем разделе нашего сайта. Он изложен настолько понятно, что усвоить его смогут школьники с разным уровнем подготовки.
После повторения базовой информации мы предлагаем попрактиковаться в выполнении соответствующих упражнений. Обширная база заданий представлена в разделе «Каталог», например, по решению задач на тему «Функция как производная своей первообразной.» Мы сгруппировали как простые, так и более сложные задачи по теме «Нахождение функции с помощью производной» и для каждой из них подробно прописали алгоритм решения, чтобы школьники смогли понять, как правильно вычислить ответ. База заданий в соответствующем разделе постоянно дополняется и обновляется.
Практиковаться в выполнении упражнений к ЕГЭ на сайте «Школково» имеют возможность все выпускники вне зависимости от региона их проживания. Если необходимо, любое задание можно сохранить в разделе «Избранное». Так учащиеся смогут оперативно вернуться к нужной задаче, еще раз повторить алгоритм ее решения и обсудить его с преподавателем или репетитором.



