Задачи по планиметрии

Точки \(M, N, P\) лежат на сторонах \(AB, BC, CA\) соответственно треугольника \(ABC\), причем \(AM:AB=BN:BC=CP:CA=1:3\). Площадь треугольника \(MNP\) равна \(15\). Найдите площадь треугольника \(ABC\).
\(\triangle ABC\) и \(\triangle MBN\) имеют общий угол \(B\), при этом \(BM=\frac23BA\), \(BN=\frac13BC\).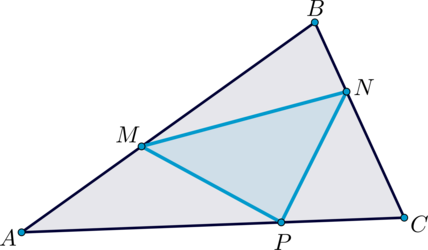
Т.к. площади треугольников, имеющих общих угол, относятся как произведения сторон, образующих этот угол, то
\[\dfrac{S_{MBN}}{S_{ABC}}=\dfrac{\frac23BA\cdot \frac13BC}{BA\cdot BC}= \dfrac29 \quad \Rightarrow \quad S_{MBN}=\dfrac29S_{ABC}\]
Аналогично рассуждая, получаем, что
\[S_{MAP}=S_{PCN}=\dfrac29S_{ABC}\]
Следовательно, \[15+3\cdot \dfrac29S_{ABC}=S_{ABC} \quad \Rightarrow \quad S_{ABC}=3\cdot 15=45.\]
Внутри треугольника \(ABC\) взяты точки \(A_1, B_1, C_1\) так, что \(B_1\) – середина \(AA_1\), \(C_1\) – середина \(BB_1\), \(A_1\) – середина \(CC_1\). Найдите отношение площадей треугольников \(A_1B_1C_1\) и \(ABC\).
Соединим точки \(A\) и \(C_1\), \(B\) и \(A_1\), \(C\) и \(B_1\).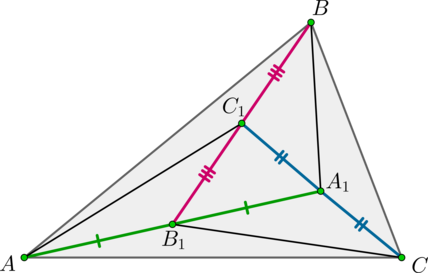
Т.к. медиана делит треугольник на два равновеликих треугольника, то
\[S_{\triangle AB_1C}=S_{\triangle A_1B_1C}=S_{\triangle A_1B_1C_1}.\]
Аналогично,
\[S_{\triangle CA_1B}=S_{\triangle C_1A_1B}=S_{\triangle AC_1B}=S_{\triangle AC_1B_1}.\]
Таким образом, все семь образовавшихся треугольников имеют одинаковые площади. Значит,
\[S_{\triangle A_1B_1C_1}:S_{\triangle ABC}=1:7.\]
\(1:7\)
Дана трапеция \(ABCD\), ее основания \(BC\) и \(AD\) равны \(2\) и \(6\) соответственно. Диагонали \(BD\) и \(AC\) пересекаются в точке \(O\). Точка \(P\) – середина \(OD\). \(S_{\bigtriangleup ABO}=9\). Найдите площадь четырехугольника \(ABCP\).
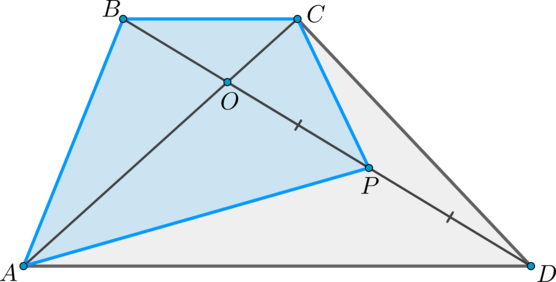
Пусть \(S_{\bigtriangleup BOC}=x\). Заметим, что \(\bigtriangleup BCO \sim \bigtriangleup AOD\) по двум углам, так как \(BC\parallel AD\), \(\angle BCA = \angle CAD\) как накрест лежащие и \(\angle BOC = \angle AOD\) как вертикальные.
Следовательно, \[\dfrac{BC}{AD} =\dfrac{BO}{OD} =\dfrac{CO}{OA} =\dfrac{2}{6} =\dfrac{1}{3}.\]
\(\dfrac{S_{\bigtriangleup ABO}}{S_{\bigtriangleup BCO}} =\dfrac{AO}{OC} =\dfrac{3}{1} \Rightarrow \ S_{\bigtriangleup ABO}=3x\), аналогично, \(S_{\bigtriangleup CDO}=3x\).
\(\dfrac{S_{\bigtriangleup COP}}{S_{\bigtriangleup CPD}} =\dfrac{OP}{PD} =\dfrac{1}{1} \Rightarrow \ S_{\bigtriangleup COP}=S_{\bigtriangleup CPD}=1,5x\).
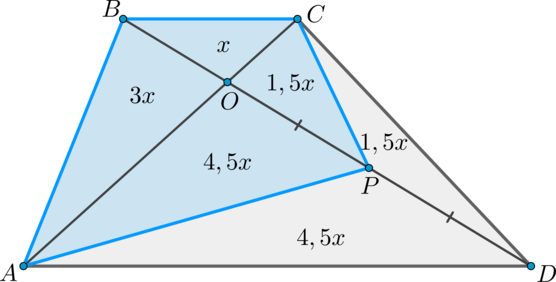
Площади подобных треугольников относятся как коэффициент подобия в квадрате, следовательно, \[\dfrac{S_{\bigtriangleup BOC}}{S_{\bigtriangleup AOD}} =\left( \dfrac{1}{3} \right)^2 =\dfrac{1}{9} \ \Rightarrow\ S_{\bigtriangleup ADO}=9x \ \Rightarrow\ S_{\bigtriangleup APO}=4,5x \ \Rightarrow\qquad S_{ABCP}=10x.\] Так как \(3x=9\), то \(x=3\) и, следовательно, \(S_{ABCP}=30\).
Внутри равностороннего треугольника со стороной \(m\) движется точка. Докажите, что сумма расстояний от этой точки до сторон треугольника не меняется, и найдите эту сумму.
Рассмотрим равносторонний \(\triangle ABC\), \(AB=m\), \(O\) – точка внутри треугольника, \(OA_1, OB_1, OC_1\) — перпендикуляры на стороны \(BC, AC, AB\) соответственно.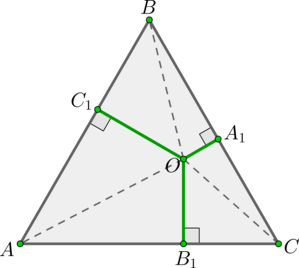
Рассмотрим \(\triangle AOB, \ \triangle BOC, \ \triangle COA\). Их площади равны \(0,5m\cdot OC_1; \ 0,5m\cdot OA_1; \ 0,5m\cdot OB_1\) соответственно. Тогда сумма их площадей равна площади всего \(\triangle ABC\), следовательно:
\[0,5m\cdot (OC_1+OA_1+OB_1)=S_{\triangle ABC}=\dfrac{\sqrt3}4m^2 \quad \Leftrightarrow \quad OC_1+OA_1+OB_1=\dfrac{\sqrt3}2m.\]
Таким образом, мы доказали, что для фиксированного равностороннего треугольника сумма постоянна, а также нашли ее.
\(\dfrac{\sqrt3}2m\)
Радиус вписанной в треугольник \(ABC\) окружности равен трети одной из его высот.
а) Докажите, что одна из сторон треугольника \(ABC\) равна среднему арифметическому двух других его сторон.
б) Найдите наибольшее возможное значение периметра такого треугольника, если одна из его сторон равна \(4\), а две другие имеют целые длины.
а) \(S_{ABC} = p\cdot r\), где \(p\) – полупериметр, а \(r\) – радиус вписанной в \(ABC\) окружности. 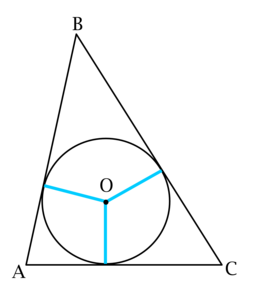
Пусть \(h\) – длина той высоты, которая равна \(3r\), \(a\) – длина стороны, высота к которой имеет длину \(h\), \(P\) – периметр треугольника \(ABC\).
В итоге имеем: \[\dfrac{1}{2}h\cdot a = S_{ABC} = p\cdot r = p\cdot\dfrac{h}{3},\] откуда \(a = \dfrac{P}{3}\), тогда \(b + c = \dfrac{2P}{3} = 2a\), где \(b\) и \(c\) длины других сторон треугольника.
б) Длины сторон треугольника \(ABC\) образуют арифметическую прогрессию: если обозначить \(a - c = d\), то \(a = c + d\), \(b = c + 2d\).
Пусть \(d > 0\). Тогда \(b\) наибольшая сторона треугольника \(ABC\) и существование треугольника \(ABC\) с длинами сторон \(a\), \(b\) и \(c\) равносильно выполнению неравенства \[b < a + c\qquad\Leftrightarrow\qquad c + 2d < 2c + d\qquad\Leftrightarrow\qquad d < c.\] Так как длины всех сторон треугольника \(ABC\) – целые числа, то \(d\) – целое, следовательно, \(d\leq c - 1\).
Так как \(c\) – меньшая из сторон, то \(c\leq 4\), тогда \(d\leq 3\), откуда \(a\leq 7\), \(b\leq 10\), тогда \[P_{\triangle ABC}\leq 4 + 7 + 10 = 21.\] При этом случай \(c = 4\), \(a = 7\), \(b = 10\) подходит, следовательно, при \(d > 0\) максимально возможный периметр равен 21.
При \(d = 0\) треугольник \(ABC\) равносторонний и \(P_{\triangle ABC} = 12 < 21\).
Случай \(d < 0\) рассматривается аналогично (меняется только то, что \(c > a > b\), следовательно, достаточно в рассуждении из случая \(d > 0\) всюду поменять местами \(b\) и \(c\)).
Таким образом, наибольший возможный периметр треугольника \(ABC\) равен 21.
б) \(21\).
Четырёхугольник \(MNPQ\) вписан в окружность, причём \(\dfrac{MN}{PQ} = \dfrac{QM}{PN}\).
а) Докажите, что точки \(N\) и \(Q\) равноудалены от прямой, содержащей \(MP\).
б) Найдите расстояние от точки \(P\) до прямой, содержащей \(MQ\), если \(MP = 4\), расстояние от \(N\) до прямой, содержащей \(MP\) равно \(1,5\), \(MQ = 3\).
а) Так как \(\dfrac{MN}{PQ} = \dfrac{QM}{PN}\), то \(MN\cdot PN = QM\cdot PQ\).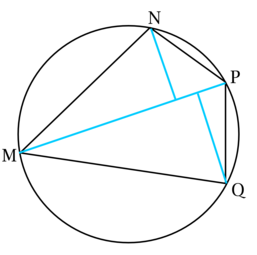
Так как \(MNPQ\) вписанный, то \(\angle MNP = 180^\circ - \angle MQP\), следовательно, \(\sin\angle MNP = \sin\angle MQP\).
В итоге \[S_{\triangle MNP} = 0,5\cdot MN\cdot PN\cdot\sin\angle MNP = 0,5\cdot QM\cdot PQ\cdot\sin\angle MQP = S_{\triangle MQP}.\]
С другой стороны, у треугольников \(MNP\) и \(MQP\) общее основание, следовательно, их площади относятся как высоты, проведённые к этому основанию, тогда эти высоты равны, значит, точки \(N\) и \(Q\) равноудалены от прямой, содержащей \(MP\).
б) В данном случае \(S_{\triangle MNP} = 0,5\cdot 4\cdot 1,5 = 3\), но \(S_{\triangle MNP} = S_{\triangle MQP}\). Обозначим расстояние от точки \(P\) до прямой, содержащей \(MQ\) через \(h\), тогда \[S_{\triangle MQP} = 3 = 0,5\cdot 3\cdot h,\] следовательно, \(h = 2\).
б) \(2\).
\(ABCD\) – выпуклый четырёхугольник, точки \(P\), \(Q\), \(R\) и \(S\) середины его сторон, причём \(PQRS\) тоже выпуклый четырёхугольник. \(A_1B_1C_1D_1\) другой выпуклый четырёхугольник с серединами сторон в точках \(P\), \(Q\), \(R\) и \(S\).
а) Докажите, что диагонали \(PQRS\) точкой пересечения делятся пополам.
б) Найдите максимально возможное значение величины \(\dfrac{S_{A_1B_1C_1D_1}}{S_{ABCD}}\).
а) Проведём диагонали \(AC\) и \(BD\).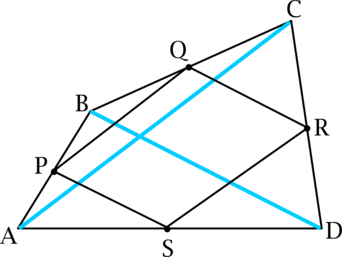
Рассмотрим треугольники \(APS\) и \(ABD\): \(PS\) – средняя линия в треугольнике \(ABD\), тогда треугольники \(APS\) и \(ABD\) подобны, причём \(\dfrac{PS}{BD} = \dfrac{1}{2}\).
Аналогично \(\dfrac{QR}{BD} = \dfrac{1}{2}\), следовательно, \(PS = QR\).
Аналогично доказывается равенство \(PQ = RS\). В итоге в выпуклом четырёхугольнике \(PQRS\) противоположные стороны равны, тогда \(PQRS\) – параллелограмм, следовательно, его диагонали точкой пересечения делятся пополам.
б) Докажем, что по взаимному расположению середин сторон выпуклого четырёхугольника его площадь восстанавливается однозначно.
Из подобия \(APS\) и \(ABD\) получаем: \[\dfrac{S_{APS}}{S_{ABD}} = \left(\dfrac{1}{2}\right)^2 = \dfrac{1}{4}.\]
Аналогично \(4S_{QCR} = S_{CBD}\), \(4S_{PBQ} = S_{ABC}\), \(4S_{SDR} = S_{ACD}\). Тогда \[S_{ABCD} = S_{ABD} + S_{CBD} = 4S_{APS} + 4S_{QCR}.\] С другой стороны, \[S_{ABCD} = S_{ABC} + S_{ACD} = 4S_{PBQ} + 4S_{SDR},\] тогда \[S_{ABCD} + S_{ABCD} = 4S_{APS} + 4S_{QCR} + 4S_{PBQ} + 4S_{SDR} \qquad\Leftrightarrow\] \[S_{APS} + S_{QCR} + S_{PBQ} + S_{SDR} = \dfrac{1}{2}S_{ABCD}.\] Но \(S_{ABCD} = S_{APS} + S_{QCR} + S_{PBQ} + S_{SDR} + S_{PQRS}\), откуда окончательно \[S_{PQRS} = \dfrac{1}{2}S_{ABCD}.\]
Таким образом, по взаимному расположению точек \(P\), \(Q\), \(R\), \(S\) однозначно восстанавливается площадь параллелограмма \(PQRS\), а значит и площадь любого выпуклого четырёхугольника с серединами сторон в точках \(P\), \(Q\), \(R\) и \(S\).
В итоге \[\dfrac{S_{A_1B_1C_1D_1}}{S_{ABCD}} = 1.\]
б) \(1\).



