Нахождение расстояния между скрещивающимися прямыми

\(\blacktriangleright\) Скрещивающиеся прямые – это прямые, через которые нельзя провести одну плоскость.
Признак скрещивающихся прямых: если первая прямая пересекает плоскость, в которой лежит вторая прямая, в точке, не лежащей на второй прямой, то такие прямые скрещиваются.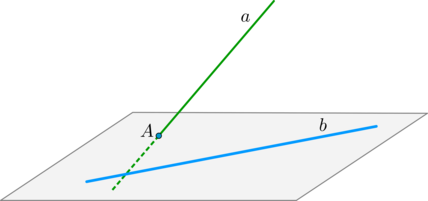
\(\blacktriangleright\) Т.к. через одну из скрещивающихся прямых проходит ровно одна плоскость, параллельная другой прямой, то расстояние между скрещивающимися прямыми — это расстояние между одной из этих прямых и плоскостью, проходящей через вторую прямую параллельно первой.
Таким образом, если прямые \(a\) и \(b\) скрещиваются, то:
Шаг 1. Провести прямую \(c\parallel b\) так, чтобы прямая \(c\) пересекалась с прямой \(a\). Плоскость \(\alpha\), проходящая через прямые \(a\) и \(c\), и будет плоскостью, параллельной прямой \(b\).
Шаг 2. Из точки пересечения прямых \(a\) и \(c\) (\(a\cap c=H\)) опустить перпендикуляр \(HB\) на прямую \(b\) (первый способ).
Или из любой точки \(B'\) прямой \(b\) опустить перпендикуляр на прямую \(c\) (второй способ).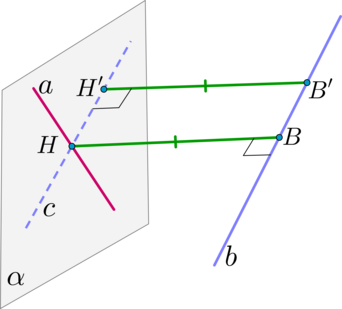
В зависимости от условия задачи какой-то из этих двух способов может быть гораздо удобнее другого.
В кубе \(ABCDA_1B_1C_1D_1\), ребро которого равно \(\sqrt{32}\), найдите расстояние между прямыми \(DB_1\) и \(CC_1\).
Прямые \(DB_1\) и \(CC_1\) скрещиваются по признаку, т.к. прямая \(DB_1\) пересекает плоскость \((DD_1C_1)\), в которой лежит \(CC_1\), в точке \(D\), не лежащей на \(CC_1\).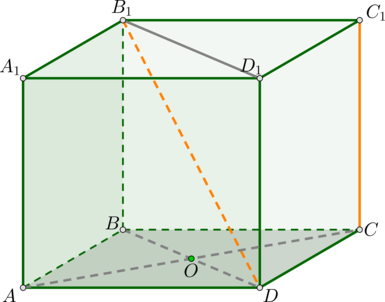
Расстояние между скрещивающимися прямыми будем искать как расстояние между прямой \(CC_1\) и плоскостью, проходящей через \(DB_1\) параллельно \(CC_1\). Т.к. \(DD_1\parallel CC_1\), то плоскость \((B_1D_1D)\) параллельна \(CC_1\).
Докажем, что \(CO\) – перпендикуляр на эту плоскость. Действительно, \(CO\perp BD\) (как диагонали квадрата) и \(CO\perp DD_1\) (т.к. ребро \(DD_1\) перпендикулярно всей плоскости \((ABC)\)). Таким образом, \(CO\) перпендикулярен двум пересекающимся прямым из плоскости, следовательно, \(CO\perp (B_1D_1D)\).
\(AC\), как диагональ квадрата, равна \(AB\sqrt2\), то есть \(AC=\sqrt{32}\cdot \sqrt2=8\). Тогда \(CO=\frac12\cdot AC=4\).
Дан куб \(ABCDA_1B_1C_1D_1\). Найдите расстояние между прямыми \(AB_1\) и \(BC_1\), если ребро куба равно \(a\).
1) Заметим, что эти прямые скрещиваются по признаку, т.к. прямая \(AB_1\) пересекает плоскость \((BB_1C_1)\), в которой лежит \(BC_1\), в точке \(B_1\), не лежащей на \(BC_1\).
Расстояние между скрещивающимися прямыми будем искать как расстояние между прямой \(BC_1\) и плоскостью, проходящей через \(AB_1\) параллельно \(BC_1\).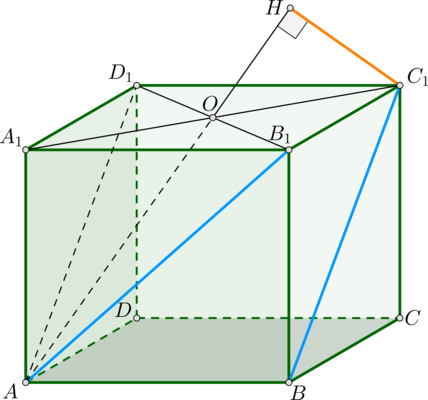
Для этого проведем \(AD_1\) — она параллельна \(BC_1\). Следовательно, по признаку плоскость \((AB_1D_1)\parallel BC_1\).
2) Опустим перпендикуляр \(C_1H\) на эту плоскость и докажем, что точка \(H\) упадет на продолжение отрезка \(AO\), где \(O\) – точка пересечения диагоналей квадрата \(A_1B_1C_1D_1\).
Действительно, т.к. по свойству квадрата \(C_1O\perp B_1D_1\), то по теореме о трех перпендикуляр проекция \(HO\perp B_1D_1\). Но \(\triangle AB_1D_1\) равнобедренный, следовательно, \(AO\) – медиана и высота. Значит, точка \(H\) должна лежать на прямой \(AO\).
3) Рассмотрим плоскость \((AA_1C_1)\).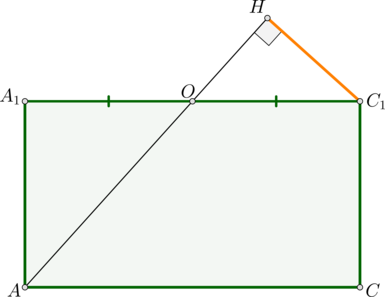
\(\triangle AA_1O\sim \triangle OHC_1\) по двум углам (\(\angle AA_1O=\angle OHC_1=90^\circ\), \(\angle AOA_1=\angle HOC_1\)). Таким образом,
\[\dfrac{C_1H}{AA_1}=\dfrac{OC_1}{AO} \qquad (*)\]
По теореме Пифагора из \(\triangle AA_1O\): \[AO=\sqrt{a^2+\dfrac{a^2}2}=\dfrac{\sqrt6}2a.\]
Следовательно, из \((*)\) теперь можно найти перпендикуляр
\[C_1H=\dfrac a{\sqrt3}.\]
\(\dfrac a{\sqrt3}\)
Дан куб \(ABCDA_1B_1C_1D_1\). Найдите расстояние между прямыми \(A_1B\) и \(AC_1\), если ребро куба равно \(\sqrt6\).
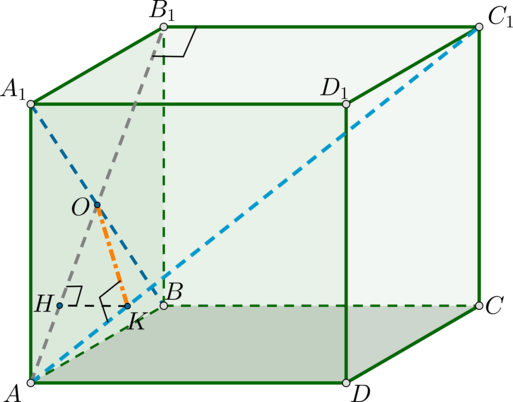
По определению угол между скрещивающимися прямыми - это угол между одной прямой и плоскостью, проходящей через вторую прямую параллельно первой. Найдем плоскость, проходящую через \(A_1B\) параллельно \(AC_1\).
Заметим, что данные прямые являются скрещивающимися. Т.к. \(B_1C_1\perp (AA_1B_1)\), то проекция наклонной \(AC_1\) на эту плоскость – это прямая \(AB_1\).
Пусть \(AB_1\cap A_1B=O\). Опустим из точки \(O\) на \(AC_1\) перпендикуляр \(OK\) и докажем, что это и есть искомое расстояние. Т.к. по определению расстояние между скрещивающимися прямыми – длина отрезка, перпендикулярного обеим прямым, то осталось доказать, что \(OK\) перпендикулярен прямой \(A_1B\).
Действительно, проведем \(KH\parallel B_1C_1\) (следовательно, \(H\in
AB_1\)). Тогда т.к. \(B_1C_1\perp (AA_1B_1)\), то и \(KH\perp
(AA_1B_1)\). Тогда по теореме о трех перпендикулярах (т.к. проекция \(HO\perp A_1B\)) наклонная \(KO\perp A_1B\), чтд.
Таким образом, \(KO\) – искомое расстояние.
Заметим, что \(\triangle AOK\sim \triangle AC_1B_1\) (по двум углам). Следовательно,
\[\dfrac{AO}{AC_1}=\dfrac{OK}{B_1C_1} \quad \Rightarrow \quad OK=\dfrac{\sqrt6\cdot \sqrt2}{2\sqrt3}=1.\]


