Нахождение углов между прямыми/плоскостями

\(\blacktriangleright\) Угол между прямыми – это острый или прямой угол.
\(\blacktriangleright\) В пространстве существует 4 типа взаимного расположения прямых: совпадают, пересекаются, параллельны, скрещиваются.
\(\blacktriangleright\) Скрещивающиеся прямые – это прямые, через которые нельзя провести одну плоскость.
Признак скрещивающихся прямых: если первая прямая пересекает плоскость, в которой лежит вторая прямая, в точке, не лежащей на второй прямой, то такие прямые скрещиваются.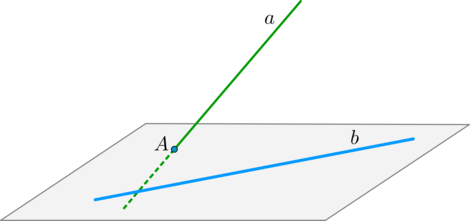
\(\blacktriangleright\) Порядок нахождения угла между скрещивающимися прямыми:
Шаг 1: через одну из двух прямых \(a\) провести плоскость, параллельную второй прямой \(b\) (напомним признак: прямая параллельна плоскости, если она параллельна какой-нибудь прямой из этой плоскости);
Шаг 2: в этой плоскости найти прямую \(c\), параллельную прямой \(b\);
Шаг 3: тогда угол между прямыми \(a\) и \(b\) будет равен углу между прямыми \(a\) и \(c\).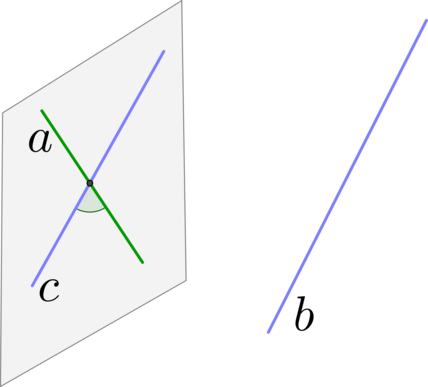
\(\blacktriangleright\) Угол между прямой и плоскостью – это угол между прямой и ее проекцией на эту плоскость (т.е. это острый или прямой угол).
\(\blacktriangleright\) Чтобы найти угол между прямой \(a\) и плоскостью \(\phi\) (\(a\cap\phi=B\)), нужно:
Шаг 1: из какой-то точки \(A\in a\) провести перпендикуляр \(AO\) на плоскость \(\phi\) (\(O\) – основание перпендикуляра);
Шаг 2: тогда \(BO\) – проекция наклонной \(AB\) на плоскость \(\phi\);
Шаг 3: тогда угол между прямой \(a\) и плоскостью \(\phi\) равен \(\angle
ABO\).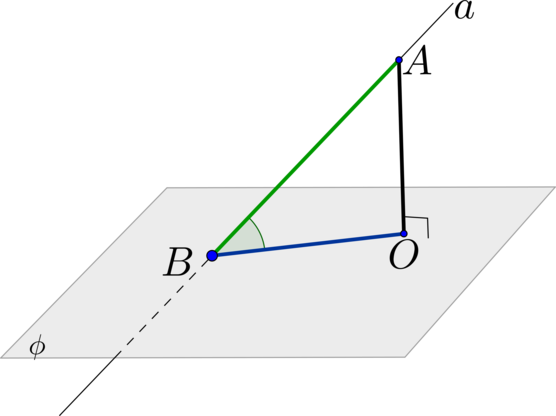
\(\blacktriangleright\) Двугранный угол – угол, образованный двумя полуплоскостями и прямой \(a\), которая является их общей границей.
\(\blacktriangleright\) Чтобы найти угол между плоскостями \(\xi\) и \(\pi\), нужно найти линейный угол (причем острый или прямой) двугранного угла, образованного плоскостями \(\xi\) и \(\pi\):
Шаг 1: пусть \(\xi\cap\pi=a\) (линия пересечения плоскостей). В плоскости \(\xi\) отметим произвольную точку \(F\) и проведем \(FA\perp a\);
Шаг 2: проведем \(FG\perp \pi\);
Шаг 3: по ТТП (\(FG\) – перпендикуляр, \(FA\) –наклонная, \(AG\) – проекция) имеем: \(AG\perp a\);
Шаг 4: угол \(\angle FAG\) называется линейным углом двугранного угла, образованного плоскостями \(\xi\) и \(\pi\).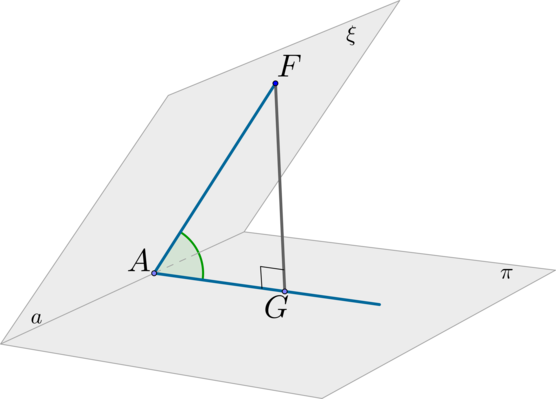
Заметим, что треугольник \(AG\) – прямоугольный.
Дан куб \(ABCDA_1B_1C_1D_1\). Найдите угол между прямыми \(A_1B\) и \(AC_1\). Ответ дайте в градусах.
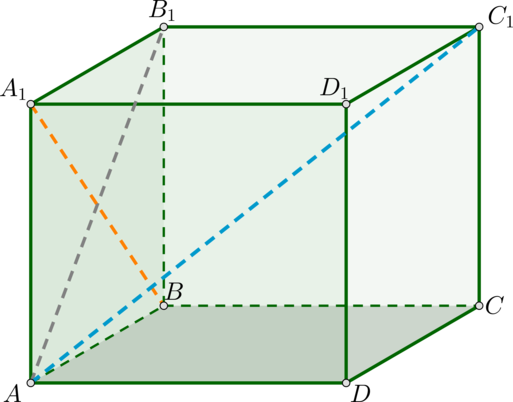
Заметим, что данные прямые являются скрещивающимися. Т.к. \(B_1C_1\perp (AA_1B_1)\), то проекция наклонной \(AC_1\) на эту плоскость – это прямая \(AB_1\). Т.к. каждая грань куба – квадрат, а диагонали квадрата перпендикулярны, то \(AB_1\perp A_1B\). Тогда по теореме о трех перпендикулярах (т.к. проекция \(AB_1\perp A_1B\)) наклонная \(AC_1\perp A_1B\). Следовательно, угол между этими прямыми равен \(90^\circ\).
Дана правильная треугольная пирамида \(DABC\), высота \(DO\) которой равна \(h\), а сторона основания \(a\). Найдите угол между основанием и боковой гранью пирамиды.
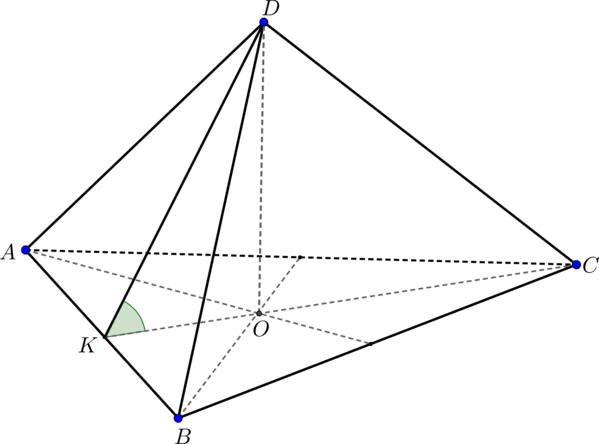
Найдем, например, угол между основанием \(ABC\) и гранью \(DAB\). Проведем \(CK\perp AB\). Т.к. пирамида правильная, то в основании лежит правильный треугольник, следовательно, \(CK\) также является и медианой. Также все боковые грани представляют собой равнобедренные треугольники, следовательно, \(DK\) – медиана, а значит, и высота. Таким образом, по определению \(\angle DKC\) является линейным углом двугранного угла между основанием \(ABC\) и гранью \(DAB\).
Т.к. пирамида правильная, то высота падает в точку пересечения медиан основания, следовательно, \(OK=\dfrac{1}{3}CK=\dfrac{1}{3}\cdot \dfrac{\sqrt3}{2}a=\dfrac{\sqrt3a}{6}\).
Тогда из прямоугольного треугольника \(DOK\) имеем \(\mathrm{tg}\, \angle DKC=\dfrac{DO}{OK}=\dfrac{2\sqrt3h}{a} \Rightarrow \angle DKC=\mathrm{arctg}\,\dfrac{2\sqrt3h}{a}\).
\(\mathrm{arctg}\,\dfrac{2\sqrt3h}{a}\).
Диагональ развертки боковой поверхности цилиндра составляет со стороной основания развертки угол \(\mathrm{arctg}\,\frac1{\pi}\). Вычислите угол между диагональю осевого сечения цилиндра и плоскостью основания.
Рассмотрим развертку цилиндра. Это прямоугольник \(ABB'A'\), где \(AB=A'B'=l\) равен образующей цилиндра, а \(AA'\) равен длине окружности основания, то есть равен \(2\pi R\) (если \(R\) – радиус основания).
Обозначим угол \(\mathrm{arctg}\,\frac1{\pi}\) за \(\phi\).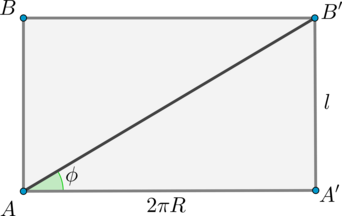
Тогда из прямоугольного треугольника \(AA'B'\) \[\mathrm{tg}\,\phi=\dfrac{A'B'}{AA'} \quad \Rightarrow
\quad \mathrm{tg}\,\phi=\dfrac{l}{2\pi R} \qquad (1)\]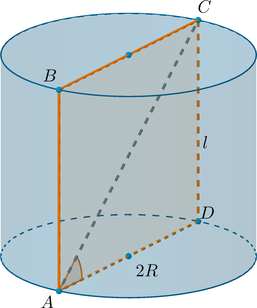
Рассмотрим осевое сечение цилиндра – это также прямоугольник \(ABCD\), где \(AB=CD=l\), а \(AD\) – диаметр основания, то есть \(AD=2R\). Т.к. \(CD\) перпендикулярен плоскости основания, то угол между \(AC\) и плоскостью основания – это угол между \(AC\) и ее проекцией \(AD\) на эту плоскость, то есть это угол \(CAD\). Тогда
\[\mathrm{tg}\,\angle CAD=\dfrac{CD}{AD} \quad \Rightarrow \quad \mathrm{tg}\,\angle CAD=\dfrac{l}{2R} \qquad (2)\]
Деля первое равенство на второе, получаем \[\dfrac{\mathrm{tg}\,\phi}{\mathrm{tg}\,\angle CAD}= \dfrac1{\pi} \quad \Rightarrow \quad \mathrm{tg}\,\angle CAD= \pi\cdot \mathrm{tg}\,\phi \quad \Rightarrow \quad \mathrm{tg}\,\angle CAD=\pi \cdot \mathrm{tg}\,\left(\mathrm{arctg}\,\dfrac1{\pi}\right)=\pi\cdot \dfrac1{\pi}=1\]
Таким образом, \(\angle CAD=45^\circ\).
\(45^\circ\)
Дана правильная шестиугольная пирамида \(SABCDEF\) с вершиной \(S\). Известно, что \(AB=1, SA=3\). Найдите угол между плоскостями \(SAB\) и \(SEF\).
(Задача от подписчиков)
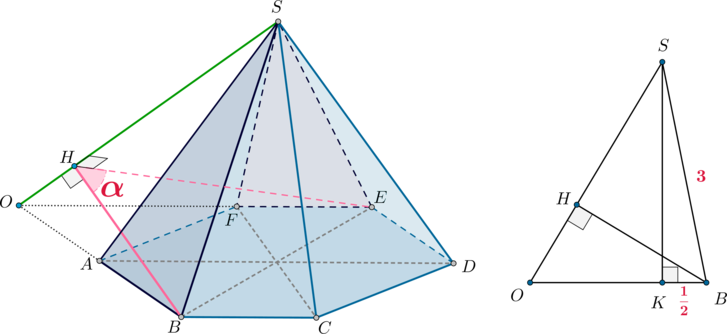
1) Продлим прямые \(AB\) и \(EF\) до пересечения в точке \(O\). Тогда \(SO\) – линия пересечения плоскостей \(SAB\) и \(SEF\). Заметим, что \(\triangle AOF\) равносторонний: углы правильного шестиугольника равны \(120^\circ\), следовательно, \(\angle OAF=\angle
OFA=180^\circ-120^\circ=60^\circ\). Следовательно, \(OA=OF=AF=1\).
Тогда \(\triangle SOE=\triangle SOB\) по двум сторонам и углу между ними (\(Ob=OE=2, \ SB=SE, \ \angle SBO=\angle SEO\)). Следовательно, если \(BH\perp SO\), то и \(EH\perp SO\). Таким образом, \(\angle
BHE=\alpha\) – линейный угол двугранного угла, образованного плоскостями \(SAB\) и \(SEF\).
2) Рассмотрим \(\triangle SOB\). \(OB=2\). Пусть \(SK\perp OB\). Тогда \(K\) – середина \(AB\), следовательно, \(KB=\frac12AB=\frac12\). Тогда по теореме Пифагора из \(\triangle SKB\): \(SK=\frac{\sqrt{35}}2\). Также по теореме Пифагора из \(\triangle SKO\): \(SO=\sqrt{11}\). Следовательно, \[SK\cdot OB=BH\cdot SO \quad\Rightarrow\quad BH=\sqrt{\dfrac{35}{11}}=EH.\]
3) Рассмотрим \(\triangle BHE\). Заметим, что по свойству правильного шестиугольника \(BE=2AB=2\). По теореме косинусов: \[\cos\alpha=\dfrac{BH^2+EH^2-BE^2}{2\cdot BH\cdot EH}=\dfrac{13}{35} \quad\Rightarrow\quad \alpha=\arccos\dfrac{13}{35}.\]
\(\arccos \frac{13}{35}\)
\(SABC\) – треугольная пирамида, в основании которой лежит равнобедренный треугольник \(ABC\) со сторонами \(10, 10\) и \(10\sqrt3\). Высота пирамиды равна \(10\) и падает в точку пересечения высот основания. Найдите угол между двумя равными гранями пирамиды.
1) Пусть \(AC=AB=10, BC=10\sqrt3, \ SO\) — высота пирамиды.
Заметим, что \(ABC\) – тупоугольный (из теоремы косинусов следует, что \(\cos \angle A<0\)). Следовательно, высоты треугольника пересекаются в одной точке, лежащей вне треугольника.
Две равные грани пирамиды – это \(SAC\) и \(SAB\). Проведем \(CH\perp SA\). Т.к. \(\triangle SAC = \triangle SAB \Rightarrow BH\perp SA\). Таким образом, \(\angle BHC= \alpha\) – искомый угол между равными гранями.
Будем искать \( \alpha\) из теоремы косинусов для \(\triangle
BHC\) (у которого \(BH=CH\)). Для этого найдем \(CH\).
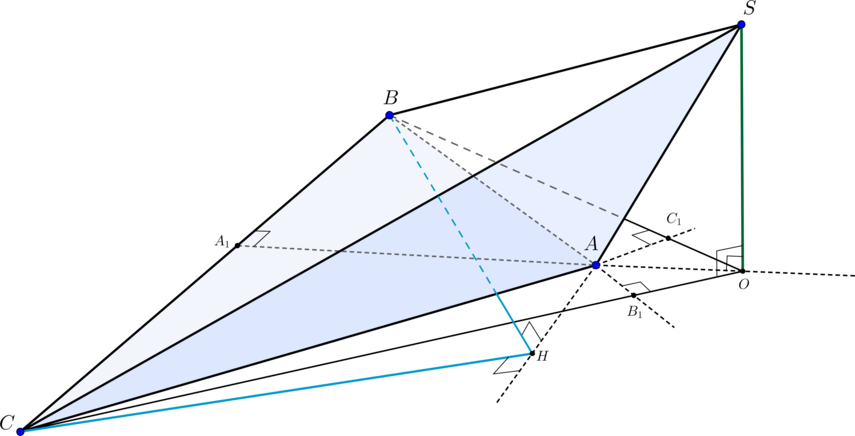
2) Пусть \(O\) – точка пересечения высот основания. По теореме косинусов для \(\triangle ABC\):
\(\cos\angle ABC=\dfrac{\sqrt3}{2} \Rightarrow \angle ABC=30^\circ\). Следовательно, \(\angle BCB_1=90^\circ-30^\circ=60^\circ\). Аналогично \(\angle CBC_1=60^\circ \Rightarrow \triangle OBC\) – равносторонний и \(OC=BC=10\sqrt3\).
По теореме Пифагора для \(\triangle SOC: \ SC=20\).
Т.к. для \(\triangle BOC \quad OA_1, BB_1, CC_1\) – медианы, то \(OA=2AA_1=10 \Rightarrow SA=10\sqrt2\).
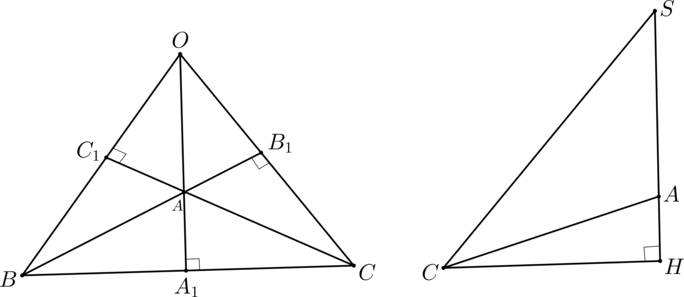
3) Заметим, что \(\triangle SAC\) – тоже тупоугольный. Найдем \(CH\):
\(CH^2=CS^2 -SH^2 =CA^2-AH^2 \Rightarrow 400-(10\sqrt2+AH)^2=100-AH^2\) (т.к. ранее мы нашли \(CS=20, SA=10\sqrt2\), а \(AC=10\) по условию)
Значит, \(AH=\dfrac{5\sqrt2}{2} \Rightarrow CH=\dfrac{5\sqrt{14}}{2}\).
Тогда по теореме косинусов для \(\triangle BHC: \ \cos \alpha =-\dfrac{5}{7} \Rightarrow \angle (SAB, SAC) = \arccos \left(-\dfrac{5}{7}\right)=\pi-\arccos \dfrac57\)
\(\pi-\arccos \dfrac{5}{7}\)
Дана правильная пятиугольная призма, сторона основания которой равна \(2\), а боковое ребро равно \(3+\sqrt5\). На ребре \(AA_1\) на расстоянии \(2\) от точки \(A\) взята точка \(M\).
1) Постройте сечение призмы плоскостью \(MBD_1\).
2) Найдите угол между плоскостью \(MBD_1\) и плоскостью основания призмы.
Замечание: отношение диагонали правильного пятиугольника к его стороне равно \(\dfrac{\sqrt5+1}2.\)
1) Назовем плоскость \(MBD_1\) плоскостью \(\alpha\).
Найдем линию пересечения \(\alpha\) и плоскости \(A_1B_1C_1\). Продлим лучи \(BM\) и \(B_1A_1\) до пересечения в точке \(O\). Тогда мы имеем две точки \(O\) и \(D_1\) в плоскости \(A_1B_1C_1\), следовательно, \(OD_1\) – линия пересечения \(\alpha\) и \(A_1B_1C_1\).
Определим, где пересекает прямая \(OD_1\) пятиугольник \(A_1B_1C_1D_1E_1\) (и пересекает ли вообще).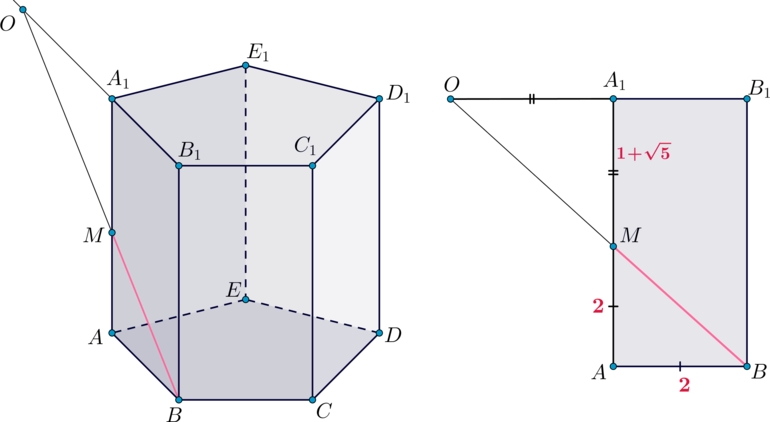
Рассмотрим плоскость \(AA_1B_1\). Так как \(AM=AB=2\), то \(\triangle
AMB\) равнобедренный. Так как \(\triangle OA_1M\sim \triangle AMB\) (по двум углам), то \(\triangle OA_1M\) тоже равнобедренный, следовательно, \(A_1M=A_1O=1+\sqrt5\).
Рассмотрим теперь плоскость \(A_1B_1C_1\):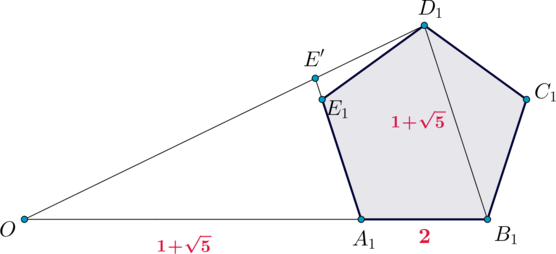
Пусть прямая \(OD_1\) пересекает прямую \(A_1E_1\) в точке \(E'\) (неизвестно, внутри отрезка \(A_1E_1\) или снаружи). Так как по свойству правильного пятиугольника \(A_1E_1\parallel B_1D_1\), то \(\triangle OE'A_1\sim \triangle OD_1B_1\) по двум углам. Следовательно, \[\dfrac{OA_1}{OB_1}=\dfrac{A_1E'}{B_1D_1}\] Так как из условия отношение диагонали правильного пятиугольника к его стороне равно \(\dfrac{\sqrt5+1}2\), то \(B_1D_1=1+\sqrt5\). Следовательно, получаем: \[A_1E'=\dfrac{(1+\sqrt5)^2}{3+\sqrt5}=2\] Следовательно, \(A_1E_1=A_1E'\), значит, \(E_1=E'\). Таким образом, плоскость \(\alpha\) пересекает грань \(A_1B_1C_1D_1E_1\) по отрезку \(D_1E_1\).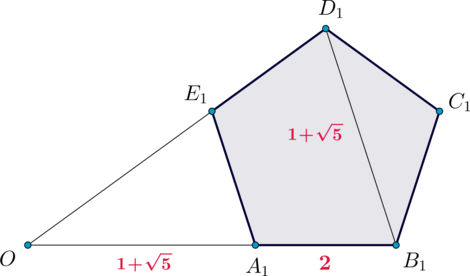
Таким образом, нам осталось найти точку пересечения плоскости \(\alpha\) с ребром \(CC_1\).
Рассмотрим плоскость \(AA_1C_1\). Она пересекает плоскость \(A_1B_1C_1\) по прямой \(A_1C_1\), параллельной прямой \(E_1D_1\), которая в свою очередь является линией пересечения \(A_1B_1C_1\) и \(\alpha\). Следовательно, \(\alpha\) пересечет \(AA_1C_1\) по прямой, параллельной \(A_1C_1\). Таким образом, в плоскости \(AA_1C_1\) проведем прямую \(MN\parallel A_1C_1\), где \(N\) – точка пересечения этой прямой с \(CC_1\). Получили сечение \(BME_1D_1N\) – пятиугольник.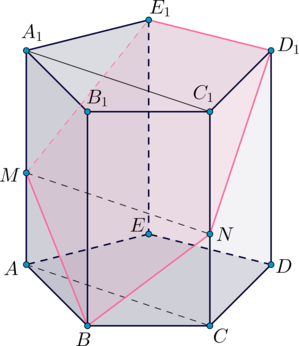
2) Так как \(MN\parallel A_1C_1\parallel AC\), то \(AM=CN\), следовательно, \(BM=BN\). Аналогично \(ME_1=ND_1\). Следовательно, перпендикуляр из \(B\) на \(MN\) упадет в середину \(MN\) - точку \(K\). Перпендикуляр из \(K\) на \(E_1D_1\) упадет в середину \(E_1D_1\) – точку \(H\) (по свойству равнобедренной трапеции: отрезок, соединяющий середины оснований равнобедренной трапеции, перпендикулярен основаниям). Следовательно, \(BH\perp E_1D_1\).
По свойству правильного пятиугольника \(B_1H\perp E_1D_1\). Следовательно, \(\angle B_1HB\) – линейный угол двугранного угла, образованного плоскостями \(\alpha\) и основания.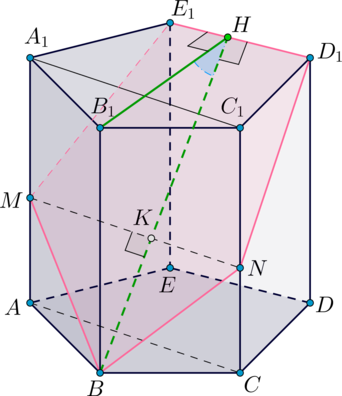
\(\triangle B_1HB\) прямоугольный (\(\angle BB_1H=90^\circ\)), следовательно, \[\mathrm{tg}\,\angle B_1HB=\dfrac{BB_1}{B_1H}\] Нужно найти \(B_1H\).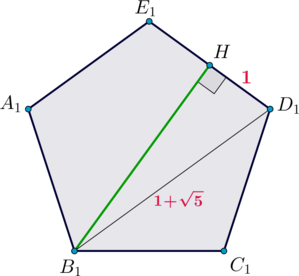
Из прямоугольного \(\triangle B_1HD_1\): \[B_1H=\sqrt{(1+\sqrt5)^2-1^2}=\sqrt{\sqrt5(2+\sqrt5)}\] Следовательно, \[\angle B_1HC=\mathrm{arctg}\,\dfrac{3+\sqrt5}{\sqrt{\sqrt5(2+\sqrt5)}}=
\sqrt{\dfrac{(3+\sqrt5)^2}{\sqrt5(2+\sqrt5)}}=
\sqrt{\dfrac{2+2\sqrt5}{\sqrt5}}\]
2) \(\mathrm{arctg}\,\sqrt{\dfrac{2+2\sqrt5}{\sqrt5}}\)


