Колебательный контур. Переменный ток

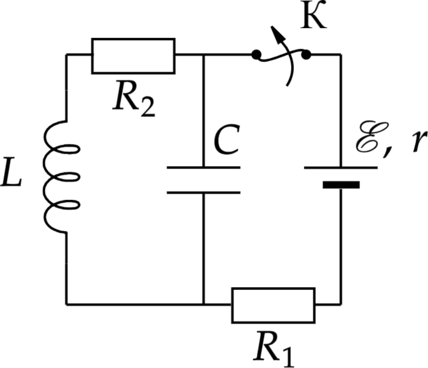
Пока ключ замкнут в цепи будет устанавливаться сила тока \[I=\dfrac{\xi}{R_1+R_2+r}, \quad (1)\] При этом напряжение на конденсаторе равно напряжению на резисторе \(R_2\), то есть \[U=\dfrac{\xi R_2}{R_1+R_2+r} \quad (2)\] На резисторе \(R_2\) будет выделятся энергия конденсатора и энергия катушки, потому что при размыкании ключа резистор \(R_1\) не будет включен в цепь и ток через него не пойдет \[W=\dfrac{LI^2}{2}+\dfrac{CU^2}{2}, \quad (3)\] Объединяя (1), (2) и (3), получим \[W=\dfrac{L\xi^2}{2(R_1+R_2+r)^2}+\dfrac{C \xi^2R_2^2}{2(R_1+R_2+r)^2}\] Отсюда индуктивность катушки \[L=\dfrac{\left(2W(R_1+R_2+r)^2- C\xi^2R_2^2\right)}{\xi^2}\] \[L=\dfrac{2\cdot 100\text{ мДж}(5\text{ Ом}+10\text{ Ом}+15\text{ Ом})^2-50\text{ мкФ}\cdot 10^4\text{ В$^2$}\cdot 225\text{ В$^2$}}{10^4\text{ В$^2$}}=6,75\text{ мГн}\]

Частота в первом случае равна: \[\nu_1=\dfrac{1}{2\pi \sqrt{LC_1}},\] где \(L\) – индуктивность катушки, \(C_1\) – ёмкость первого конденсатора.
При подключении второго конденсатора ёмкостью \(C_2\), ёмкость контура равна \[C=C_1+C_2\] А частота во втором случае равна \[\nu_1=\dfrac{1}{2\pi \sqrt{LC_1}},\] Найдем отношение частот \[\dfrac{\nu_1}{\nu_2}=\dfrac{\dfrac{1}{2\pi \sqrt{LC_1}}}{\nu_1=\dfrac{1}{2\pi \sqrt{L(C_1+C_2)}}}=\sqrt{\dfrac{C_1+C_2}{C_1}}\] Возведем обе части в квадрат и выразим ёмкость второго конденсатора \[\left(\dfrac{\nu_1}{\nu_2}\right)^2=\dfrac{C_1+C_2}{C_1} \Leftrightarrow \dfrac{C_1+C_2}{C_1}=4 \Rightarrow C_2=3C_1=6\text{ мкФ}\]

ТАк как конденсатор первоначально заряжен, то заряд на нем меняется по закону: \[q=q_m\cos(\omega t),\] где \(q_m\) – максимальный заряд на конденсаторе, \(\omega\) – циклическая частота колебани, \(t\) – время.
Значит энергия электрического поля изменяется по закону \[W_\text{ эл}=\dfrac{q^2}{2C}=\dfrac{(q_m\cos(\omega t))^2}{2C}\] Так как по условию энергия электрического поля должна равняться энергии магнитного поля, то энергия электрического поля равна половине максимальной энергии \[W_\text{ эл}=0,5W \Leftrightarrow \dfrac{(q_m\cos(\omega t))^2}{2C}=\dfrac{q_{m}^2}{4C} \Rightarrow \cos{(\omega t)}=\dfrac{\sqrt{2}}{2} \Rightarrow \omega t=\dfrac{\pi}{4}\] Циклическая частота же равна \(\omega=\dfrac{2\pi}{T}\), следовательно, время равно \[t=\dfrac{\pi}{4\omega}=\dfrac{T}{8}\] Период колебаний находится по формуле \[T=2\pi\sqrt{LC}\] Откуда время \[t=\dfrac{\pi}{4}\sqrt{LC}=\dfrac{3,14}{4}\sqrt{3 \cdot 10^{-6}\text{ Ф}\cdot 12\cdot 10^{-2}\text{ Гн}}=471 \text{ мкс}\]

Частота в первом случае равна: \[\nu_1=\dfrac{1}{2\pi \sqrt{LC_1}},\] где \(L\) – индуктивность катушки, \(C_1\) – ёмкость первого конденсатора.
При подключении второго конденсатора ёмкостью \(C_2\), ёмкость контура равна \[C=\dfrac{C_1C_2}{C_1+C_2}\] А частота во втором случае равна \[\nu_2=\dfrac{1}{2\pi \sqrt{L\dfrac{C_1C_2}{C_1+C_2}}},\] Найдем отношение частот \[\dfrac{\nu_2}{\nu_1}=\sqrt{\dfrac{(C_1+C_2)C_1}{C_1C_2}}\] По условию \(C_2=2C_1\), следовательно, последнее уравнение можно переписать в виде \[\dfrac{\nu_2}{\nu_1}=\sqrt{\dfrac{3C_1^2}{2C_1^2}}=\sqrt{\dfrac{3}{2}}\] Также по условию \(\nu_2=\nu_1+200\text{ Гц}\), значит \[1+\dfrac{200\text{ Гц}}{\nu_1}=\sqrt{1,5}\] Откуда начальная частота \[\dfrac{200\text{ Гц}}{\nu_1}=\sqrt{1,5}-1 \Leftrightarrow \nu_1=\dfrac{200\text{ Гц}}{\sqrt{1,5}-1}\approx 890\text{ Гц}\]