11.10 Комбинации нескольких графиков
Ошибка.
Попробуйте повторить позже
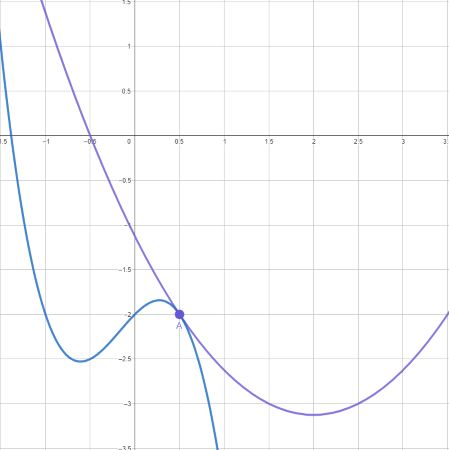
На рисунке изображены графики двух функций вида которые
пересекаются в точке
Найдите
Первый способ.
Пусть — уравнение первой прямой,
— уравнение второй прямой.
Заметим, что первая прямая проходит через точки и
Если прямая проходит через точку на плоскости, то
координаты этой точки обращают уравнение этой прямой в верное равенство. Тогда получаем систему из двух
уравнений:
Значит, уравнение первой прямой имеет вид
Вторая прямая проходит через точки и
Следовательно, получаем следующую систему:
Значит, уравнение второй прямой имеет вид
Обе прямые проходят через точку по условию, тогда имеем систему:
Второй способ.
Если прямая на плоскости проходит через две точки
и
то можем составить ее каноническое
уравнение:
На рисунке видно, что одна из прямых проходит через точки и
Тогда имеем:
Другая прямая проходит через точки и
Аналогично запишем ее каноническое уравнение:
Если прямая проходит через точку на плоскости, то координаты этой точки обращают уравнение прямой в верное равенство.
Обе прямые проходят через точку по условию, тогда имеем систему:
Ошибка.
Попробуйте повторить позже
На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.
Способ 1.
Найдём уравнение функции график которой представляет из себя убывающую прямую, на которой отмечены
точки
Найдём угловой коэффициент:
Получим уравнение функции в виде
Найдём значение подставив в уравнение точку
Получится уравнение
Найдём уравнение функции график которой представляет из себя возрастающую прямую, на которой
отмечены точки
Найдём угловой коэффициент:
Получим уравнение функции в виде
Найдём значение подставив в уравнение точку
Получится уравнение
Теперь решим уравнение
Тогда ордината точки пересечения прямых равна
Способ 2.
По картинке видим, что целые точки и
принадлежат графику первой прямой
поэтому можем
составить систему из двух уравнений:
Также целые точки и
принадлежат графику второй прямой
поэтому можем составить
систему из двух уравнений:
Значит, функции имеют вид
Аналогично первому способу решаем уравнение и получаем ответ.
Ошибка.
Попробуйте повторить позже
На рисунке изображены графики двух линейных функций, пересекающиеся в
точке Найдите абсциссу точки
Найдем уравнения прямых.
Определим коэффициенты и
для нижней прямой. Найдём
как тангенс угла наклона прямой:
Чтобы найти подставим одну из точек на прямой в уравнение с уже рассчитанным коэффициентом
Подставим точку
Значит, первая функция имеет вид
Теперь определим коэффициенты и
для верхней прямой. Найдём
как тангенс угла наклона прямой:
Чтобы найти подставим одну из точек на прямой в уравнение с уже расcчитанным коэффициентом
Подставим точку
Значит, вторая функция имеет вид
Теперь найдем абсциссу точки пересечения двух прямых.
Ошибка.
Попробуйте повторить позже
На рисунке изображены графики двух линейных функций, пересекающиеся в
точке Найдите абсциссу точки
Найдем уравнения прямых.
Определим коэффициенты и
для нижней прямой. Найдём
как тангенс угла наклона прямой:
Чтобы найти подставим одну из точек на прямой в уравнение с уже рассчитанным коэффициентом
Подставим точку
Значит, первая функция имеет вид
Теперь определим коэффициенты и
для верхней прямой. Найдём
как тангенс угла наклона прямой:
Чтобы найти подставим одну из точек на прямой в уравнение с уже рассчитанным коэффициентом
Подставим точку
Значит, вторая функция имеет вид
Теперь найдем абсциссу точки пересечения двух прямых.
Ошибка.
Попробуйте повторить позже
На рисунке изображены графики функций и
которые пересекаются в точках
и
Найдите
Для начала разберемся, какой из графиков какой функции соответствует.
Координата по вершины параболы
равна
что
соответствует правой параболе.
Любую параболу вида можно представить в виде
Здесь — координаты ее вершины. По картинке несложно видеть, что
вершина левой параболы
имеет координаты
значит функция имеет
вид
Также по картинке видно, что в точке -4 функция равна 1. Это условие
можно записать следующим образом:
Теперь мы полностью восстановили функцию она имеет вид
Найдем точки пересечения и
Пересечение, соответствующее это точка
Тогда координата
точки
равна 3.
Ошибка.
Попробуйте повторить позже
На рисунке изображены графики функций и
которые
пересекаются в точке
Найдите абсциссу точки
Источники:
По картинке видим, что точка принадлежит графику функции
следовательно,
Посмотрим теперь на график функции Это прямая, которой принадлежат
точки
и
Найдем угловой коэффициент:
Найдем подставив в уравнение
точку
и
Найдем абсциссу точки приравняв
и
Ошибка.
Попробуйте повторить позже
На рисунке изображены графики функций вида и
пересекающиеся в точках
и
Найдите абсциссу точки
Найдем значения параметра и
Чтобы найти точки пересечения, необходимо приравнять функции:
Точку с абсциссой
мы уже видим на рисунке, поэтому в ответ
запишем корень
Ошибка.
Попробуйте повторить позже
На рисунке изображены графики функций видов и
пересекающиеся в точках
и
Найдите абсциссу точки
Для начала рассмотрим функцию
Переходим к функции Видим, что
так как прямая пересекает
ось ординат в точке
Подставив координаты точки в уравнение
получим
откуда
Приравниваем восстановленные функции:
Точка пересечения графиков с абсциссой уже изображена на рисунке,
поэтому нам подходит точка с абсциссой
Ошибка.
Попробуйте повторить позже
На рисунке изображены графики функций видов и
пересекающиеся в точках
и
Найдите абсциссу точки
начнем с параболы: поэтому коэффициент
Прямая:
Приравниваем две функции:
Точка пересечения у нас уже изображена на рисунке, поэтому нам
подходит точка
Ошибка.
Попробуйте повторить позже
На рисунке изображены графики функций и
которые пересекаются в точках
и
Найдите
Заметим, что любую квадратичную функцию можно представить в виде
Здесь — координаты вершины параболы. По графику видно, что
Найдём подставив точку
в уравнение параболы:
Получим уравнение параболы
Найдём уравнение линейной функции
Ее график проходит через точки и
Найдём значение углового коэффициента:
Значение коэффициента равно 3, поскольку прямая пересекает ось ординат в точке
Получим уравнение функции
Чтобы найти координаты точки надо решить уравнение
Первое значение соответствует абсциссе точки
тогда второе — абсциссе точки
Найдём её ординату, подставив
в уравнение любой из функций. Подставим в
Ошибка.
Попробуйте повторить позже
На рисунке изображены графики функций и
которые пересекаются в точках
и
Найдите ординату
точки
По картинке видно, что график функции проходит через точки
и
Если график функции проходит
через определенную точку, то ее координаты обращают уравнение функции в верное равенство. Значит, мы можем составить
систему из трех уравнений:
Из первого уравнения следует, что Тогда, подставив этот результат во второе уравнение, получим
Подставив и
в третье уравнение, получим
Тогда можем найти
Значит, мы нашли уравнение функции
По условию графики функций и
пересекаются в точках
и
Тогда координаты точки
обращают уравнения функций
и
в верные равенства:
Тогда ордината точки
равна
Ошибка.
Попробуйте повторить позже
На рисунке изображены графики функций
которые пересекаются в точках и
Найдите
Парабола на рисунке получается из параболы отражением относительно
оси абсцисс с получением параболы
поднятием на 1 вверх с
получением параболы
и сдвигом влево на 2 с получением параболы
Следовательно, ее уравнение
Значит, так как то имеем:
Найдем координаты точки
Следовательно,
Ошибка.
Попробуйте повторить позже
На рисунке изображены графики двух функций: одна из них линейная, другая — вида
Найдите абсциссу точки пересечения графиков этих функций. Если таких точек несколько, в ответе укажите наименьшую абсциссу.
Для решения найдём уравнения обеих функций, после чего решим уравнение, приравняв эти функции, что и будет означать пересечение графиков функций.
Найдём уравнение линейной функции. Заметим, что прямая проходит через точки и
Тогда угловой
коэффициент можно найти по формуле
Получим уравнение прямой
Для нахождения свободного коэффициента подставим произвольную точку на прямой в это уравнение. Подставим точку
Получаем уравнение прямой
Найдём уравнение второй функции. Заметим, что график имеет вершину из чего можно сделать вывод, что
Чтобы найти
подставим в полученную функцию
координаты точки
которая находится на
графике.
Получаем уравнение второй функции
Приравняем полученные функции:
Возведём в квадрат обе части уравнения, отметив, что правая чать должна быть неотрицательной, то есть
Поскольку решение уравнения существует при , получим единственное решение
Ошибка.
Попробуйте повторить позже
На рисунке изображены графики функций и
которые пересекаются в точках
и
Найдите абсциссу точки
Заметим, что область определения функции совпадает с
областью определения функции
и равна
Из графика видно, что определена на
откуда получаем
Тогда функция примет вид
По графику то есть
По графику то есть
Найдем отличную от точку пересечения графиков функций
и
Из последней системы получаем Тогда абсцисса точки
пересечения
графиков равна 8.
Ошибка.
Попробуйте повторить позже
На рисунке изображены графики функций и
которые пересекаются в точках
и
Найдите
Найдём уравнение функции По графику видно, что
поскольку функция увеличивается на 1 при увеличении
аргумента на 1. Также прямая пересекает ось ординат в точке
откуда
Тогда уравнение прямой имеет
вид
Найдём уравнение функции Подставим точку
на графике в уравнение функции:
Тогда уравнение корня имеет вид
Найдём координаты точек пересечения графиков, приравняв функции:
Сделаем замену и получим квадратное уравнение:
Сделаем обратную замену и получим совокупность
Точке соответствует координата
Подставим её в уравнение
и получим
Ошибка.
Попробуйте повторить позже
На рисунке изображены графики функций и
которые пересекаются в точках
и
Найдите ординату
точки
Определим какой из графиков, то есть «верхний» или «нижний», принадлежит функции Заметим, что
значит, график функции
проходит через точку
Тогда функции
соответствует «верхний»
график.
Восстановим уравнение функции Заметим, что «нижний» график проходит через точку
следовательно,
справедливо равенство
Также график функции проходит через целые точки
и
Значит, можем составить систему
уравнений:
Таким образом, мы полностью восстановили уравнение функции
Теперь найдем абциссы точек пересечения графиков функций и
Значит, абсцисса точки равна 7. Тогда ордината точки
равна
Ошибка.
Попробуйте повторить позже
На рисунке изображены графики функций и
которые
пересекаются в точках
и
Найдите абсциссу точки
По условию график функции проходит через точку
значит, координаты точки
обращают уравнение
в верное равенство, то есть
Тогда уравнение можно записать в виде
По условию график функции проходит через точки
и
Значит, координаты точек
и
обращают уравнение
в верное равенство, то есть
Тогда уравнение можно записать в виде
Так как — вторая точка пересечения графиков функций
и
то
Поскольку — абcцисса точки
то абсцисса точки
равна
Ошибка.
Попробуйте повторить позже
На рисунке изображены графики функций и
которые пересекаются в точках
и
Найдите
ординату точки
Способ 1.
Подставим точку расположенную на графике гиперболы, в функцию
Найдём коэффициент по точкам на графике линейной функции
Найдём подставив точку
Найдём точки пересечения, приравняв и
Решим данное уравнение методом переброски коэффициента. Решим уравнение
По теореме Виета легко находятся корни и
Тогда у исходного уравнения корни равны
Видно, что точке соответствует координата
тогда точке
— координата
Найдём ординату, подставив
в
Способ 2.
По картинке видим, что целая точка принадлежит графику гиперболы
и целые точки
и
принадлежат графику прямой
Можем полностью восстановить вид обеих
функций:
Получили, что
Найдем теперь абсциссы точек пересечения
и
Точка находится правее точки
следовательно, ей соответствует большая координата по оси абсцисс
Осталось
найти ординату точки
Ошибка.
Попробуйте повторить позже
На рисунке изображены графики функций и
которые
пересекаются в точках
и
Найдите
Восстановим уравнение функции Ее график проходит через точку
Значит, можем составить
уравнение:
Тогда функция имеет вид
Восстановим уравнение функции Ее график проходит через точку
следовательно,
Также график проходит через точку
следовательно,
Значит, функция имеет вид
Найдем абсциссу точки
Ошибка.
Попробуйте повторить позже
Даны функции и
Определите,
при каком значении
графики
и
пересекаются ровно в одной
точке, причём с положительной абсциссой.
Пусть графики функций пересекаются в точке Тогда для выполнения
касания в ней нам требуется записать систему из трёх условий — о равенстве
значений функций в точке
и равенстве значений производной в этой же
точке (ну и помним про положительность абсциссы):
|
|
|
|
Рассмотрим последнее уравнение системы отдельно:
Помня об условии оставляем корень
Подставим его во
второе уравнение системы и получим ответ: