Ошибка.
Попробуйте повторить позже
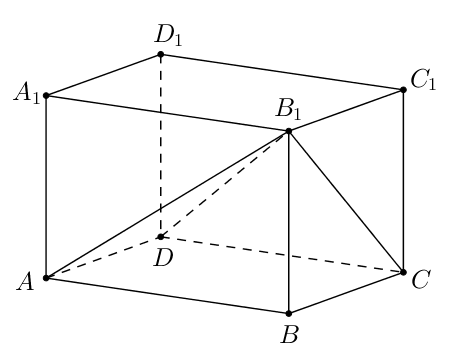
Найдите объём многогранника, вершинами которого являются вершины
прямоугольного параллелепипеда
у которого
Источники:
Многогранник, объём которого необходимо найти, является пирамидой, высотой
которой является а основание представляет собой прямоугольник
Следовательно, искомый объём равен
Ошибка.
Попробуйте повторить позже
Объём куба равен 32. Найдите объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины.
Источники:
Данная призма имеет такую же высоту, что и куб. Тогда поскольку куб — это тоже
призма, то объём призмы будет во столько раз меньше объёма куба, во сколько
раз будет меньше его основание, чем основание куба, ведь для призмы
Заметим, что плоскость проходит по средней линии основания, ведь прямая, проходя параллельно боковому ребру через середину ребра верхнего основания, будет также проходить и через середину ребра нижнего основания. А поскольку средняя линия отсекает четверть площади от треугольника, площадь которого составляет половину площади основания куба, то основание призмы в 8 раз меньше основания куба. Таким образом, объём призмы равен
Ошибка.
Попробуйте повторить позже
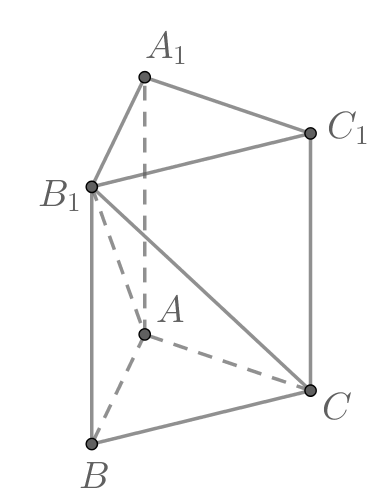
Найдите объём многогранника, вершинами которого являются вершины
правильной треугольной призмы
площадь основания
которой равна 6, а боковое ребро равно 9.
Источники:
Ошибка.
Попробуйте повторить позже
Куб описан около сферы радиуса 3. Найдите объем куба.
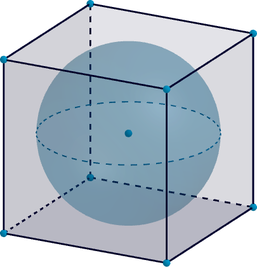
Так как сфера вписана в куб, то сторона куба равна диаметру сферы. Следовательно, сторона куба равна Тогда объем
куба равен
Ошибка.
Попробуйте повторить позже
– куб. Найдите угол между прямыми, содержащими отрезки
и
. Ответ
дайте в градусах.
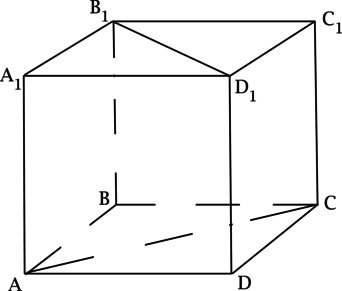
Прямая параллельна прямой
, тогда угол между
и
равен углу между
и
, но
и
– диагонали квадрата, тогда они пересекаются под прямым углом, следовательно
ответ
.
Ошибка.
Попробуйте повторить позже
В квадрате диагонали пересекаются в точке
точка
не лежит в плоскости квадрата, при этом этом
Найдите угол между плоскостями
и
если
а
Ответ дайте в градусах.
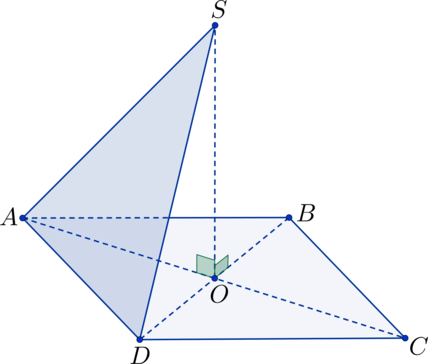
По условию имеем:
Кроме того, так как
— точка пересечения диагоналей квадрата, и
— общая сторона двух
треугольников.
Тогда прямоугольные треугольники и
равны по двум сторонам и углу между ними. Следовательно,
и
— равнобедренный.
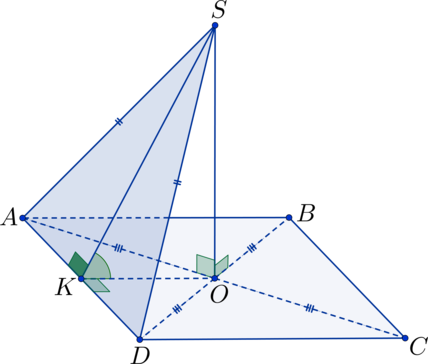
Далее, точка — середина
тогда
— высота в треугольнике
а
— высота в треугольнике
Следовательно,
— линейный угол искомого двугранного угла.
В имеем:
Тогда — равнобедренный прямоугольный треугольник и
Ошибка.
Попробуйте повторить позже
В кубе точка
лежит на ребре
а точка
лежит на ребре
причем
Найдите квадрат косинуса двугранного угла, образуемого плоскостями
и
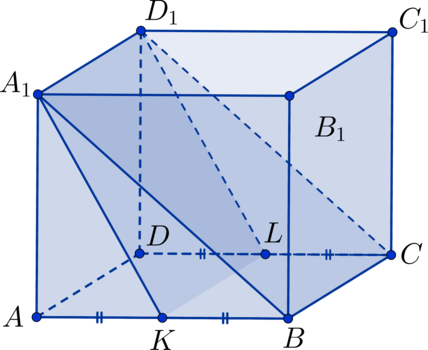
Так как три ребра, выходящие из одной вершины куба, попарно взаимно перпендикулярны, то ребро перпендикулярно
плоскости грани
и
, тогда величина линейного угла
совпадает с искомым
двугранным углом.
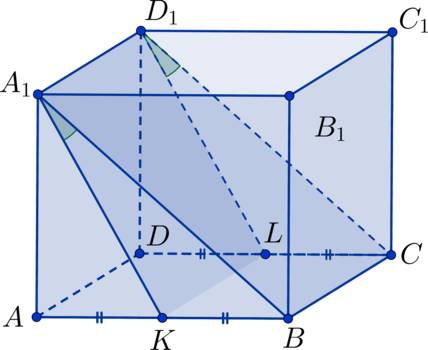
Примем сторону куба за и рассмотрим треугольник
:
,
– диагональ квадрата
, а сторону
можно найти по теореме Пифагора из треугольника
:
Зная все три стороны в треугольнике , можно воспользоваться теоремой косинусов, чтобы найти косинус искомого
угла:
.
Ошибка.
Попробуйте повторить позже
Объем правильной треугольной пирамиды равен . Найдите объем пирамиды, боковые ребра которой
являются апофемами исходной пирамиды.

Пусть – пирамида, боковые ребра которой являются апофемами исходной пирамиды
.
тоже является правильной пирамидой, так как вершины треугольника
являются
серединами сторон треугольника
, а значит стороны треугольника
являются
средними линиями треугольника
стороны треугольника
относятся к
соответствующим сторонам треугольника
как
их площади состоят в
отношении
. Высота искомой пирамиды совпадает с высотой исходной пирамиды
их
объемы относятся также, как их площади
объем искомой пирамиды равен
.
Ошибка.
Попробуйте повторить позже
Объем шара равен Чему будет равна площадь поверхности шара, если его радиус увеличить на
По формуле объема шара с радиусом имеем:
Радиус нового шара равен
Тогда найдем площадь поверхности:
Ошибка.
Попробуйте повторить позже
Площадь боковой поверхности конуса равна а площадь основания равна
Найдите длину образующей
конуса.
Если радиус окружности, лежащей в основании конуса, обозначить за а длину образующей за
то площадь основания и
площадь боковой поверхности конуса выразятся по формулам:
Из первой формулы получаем:
Из второй формулы получаем:
Ошибка.
Попробуйте повторить позже
Площадь боковой поверхности конуса равна а площадь боковой поверхности усеченного конуса с такими же большим
основанием и углом наклона образующей к плоскости основания равна
Найдите высоту усеченного конуса, если высота
исходного конуса равна 10.
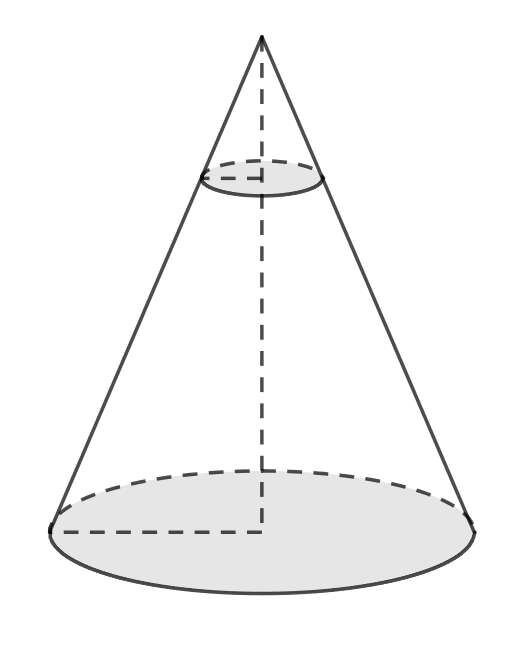
Площадь боковой поверхности меньшего конуса, который дополняет усеченный конус до полного, равна разности их площадей поверхностей:
Отношение площадей боковых поверхностей большого и малого конусов равно квадрату коэффициента подобия треугольников, являющихся осевыми сечениями этих конусов:

Тогда отношение высот конусов равно коэффициенту подобия:
Отсюда найдем высоту малого и усеченного конусов:
Ошибка.
Попробуйте повторить позже
Дан прямоугольный параллелепипед с ребрами и
. Найдите его диагональ.
Пусть .
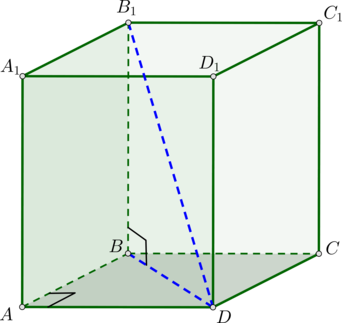
По теореме Пифагора из прямоугольного треугольника (
) имеем:
.
Из прямоугольного треугольника (
) по теореме Пифагора
.
Подставляя из первого равенства во второе, получим:
Ошибка.
Попробуйте повторить позже
Дана пирамида с высотой
, в основании которой лежит прямоугольный треугольник с
прямым углом
. Найдите угол между прямыми
и
. Ответ дайте в градусах.
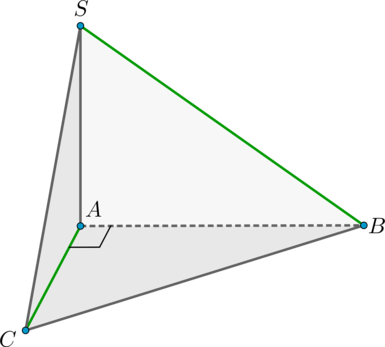
Так как – высота пирамиды, то
. Заметим, что
– проекция наклонной
на плоскость
. Следовательно, по теореме о трех перпендикулярах (так как
) наклонная
перпендикулярна
, то есть угол между ними равен
.
Ошибка.
Попробуйте повторить позже
– параллелепипед,
– квадрат со стороной
, точка
– основание
перпендикуляра, опущенного из точки
на плоскость
, кроме того
– точка пересечения
диагоналей квадрата
. Известно, что
. Найдите угол между плоскостями
и
. Ответ дайте в градусах.
Построим перпендикулярно
как показано на рисунке.
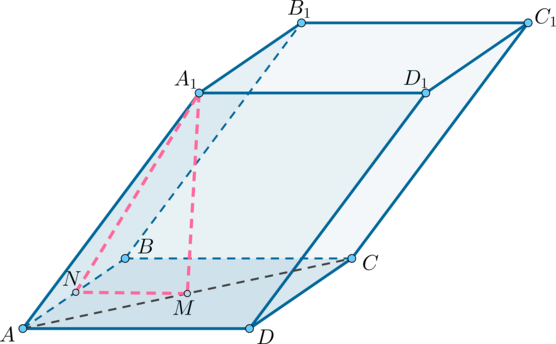
Так как – квадрат со стороной
и
и
, то
. Так как
– точка пересечения диагоналей квадрата, то
– середина
, следовательно,
– средняя
линия и
.
– проекция
на плоскость
, причем
перпендикулярен
, тогда по теореме
о трех перпендикулярах
перпендикулярен
и угол между плоскостями
и
есть
.
Ошибка.
Попробуйте повторить позже
Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника
прямые).
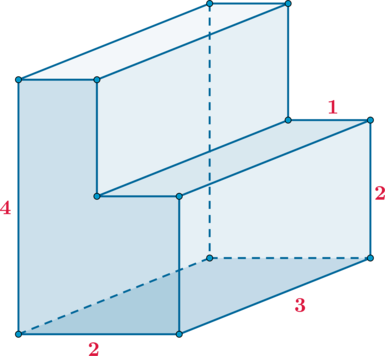
Заметим, что можно разбить данный многогранник на два непересекающихся прямоугольных
параллелепипеда и
:
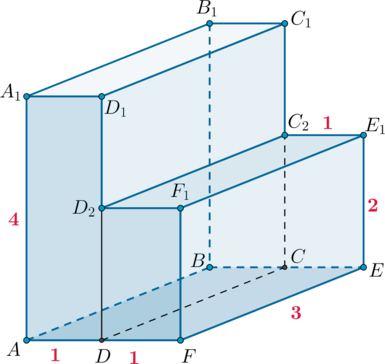
Тогда объем первого параллелепипеда будет равен , а объем второго
.
Следовательно, объем всего многогранника будет равен
.
Ошибка.
Попробуйте повторить позже
Дан куб Найдите угол между прямыми
и
Ответ
дайте в градусах.
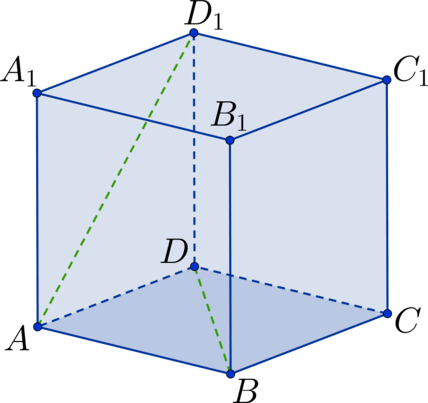
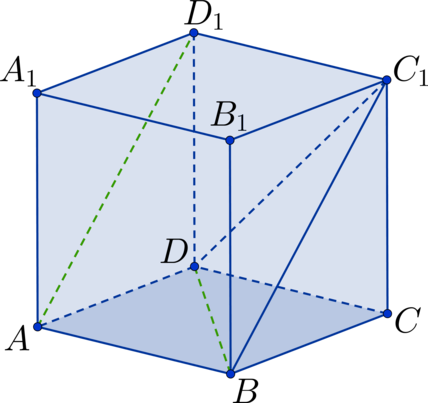
Заметим, что тогда рассмотрим треугольник
в котором
необходимо определить
Он состоит из диагоналей соответствующих
квадратов. Так как квадраты между собой равны, то равны и диагонали,
следовательно,
— равносторонний треугольник. Тогда
Ошибка.
Попробуйте повторить позже
Дан куб . Точка
– середина стороны
, а точка
– середина стороны
. Найдите угол между прямыми
и
. Ответ дайте в градусах.
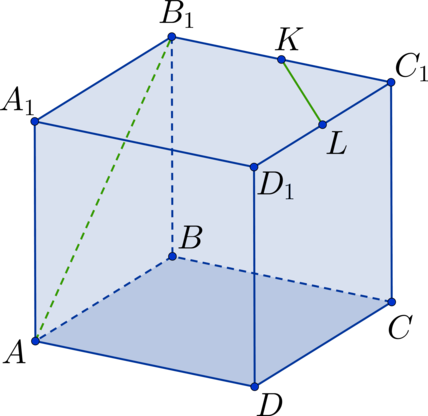
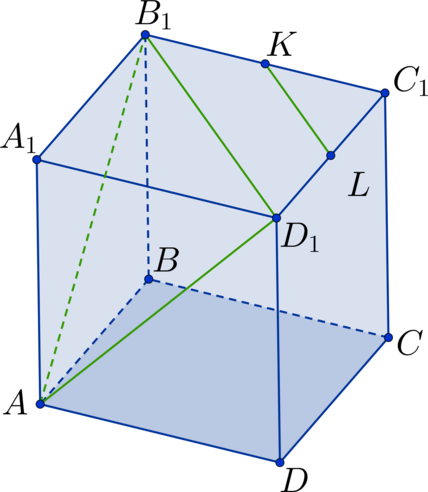
Проведем диагональ в квадрате
. Тогда
– средняя линия в
– искомый угол. Рассмотрим
. Он состоит из диагоналей
соответствующих квадратов
треугольник является равносторонним
.
Ошибка.
Попробуйте повторить позже
В основании пирамиды лежит прямоугольный треугольник с прямым углом
.
Точка
– центр описанной вокруг треугольника
окружности,
– высота
пирамиды. Найдите объем пирамиды, если известно, что
,
,
.
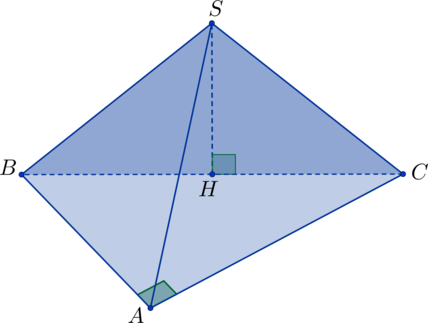
Центр описанной вокруг прямоугольного треугольника окружности лежит на гипотенузе и делит
ее пополам – радиусы описанной окружности. В прямоугольном
треугольнике
по теореме Пифагора:
. Треугольник
– прямоугольный, т.к.
(
– высота), тогда
по теореме Пифагора можно найти
:
.
Теперь найдем объем пирамиды:
Ошибка.
Попробуйте повторить позже
В прямоугольной пирамиде известно, что
— высота пирамиды,
— прямоугольная трапеция с прямыми
углами
и
Найдите объем пирамиды, если
а

и
— прямоугольные треугольники, следовательно,
Таким образом,
Тогда можем найти площадь основания:
Значит,
Ошибка.
Попробуйте повторить позже
Найдите объем правильного тетраэдра, если одна из его апофем равна .

В правильном тетраэдре все грани являются равносторонними треугольниками. Высота тетраэдра
падает в точку пересечения медиан равностороннего треугольника (она же является точкой пересечения
биссектрис, высот и т.д.; далее в решении задачи нас будет интересовать точка пересечения медиан),
лежащего в основании.
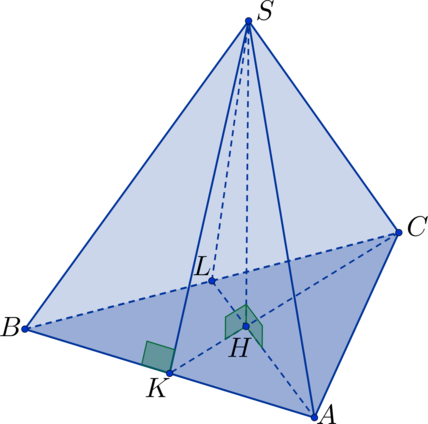
Пусть – правильный тетраэдр,
– апофема, лежащая в грани
. Она же является
медианой, проведенной к стороне
. Тогда, если ребро тетраэдра обозначить за
, то
высота
в равностороннем треугольнике выразится как
.
и
– медианы в треугольнике
,
– точка пересечения
и
,
– высота в тетраэдре. Медианы точкой пересечения делятся на отрезки,
состоящие в отношении
, где больший отрезок лежит между соответствующей вершиной
треугольника и точкой пересечения медиан. Тогда рассмотрим прямоугольный треугольник
:
, т.к. все равносторонние треугольники равны между собой и
следовательно также равны между собой их высоты.
, тогда найдем
по
теореме Пифагора:
. Наконец, найдем объем правильного
тетраэдра:



