Центральные и вписанные углы окружности

\(\blacktriangleright\) Центральный угол – угол, вершина которого лежит в центре окружности.
Центральный угол равен дуге, на которую он опирается.
\(\blacktriangleright\) Вписанный угол – угол, вершина которого лежит на окружности.
Вписанный угол равен половине дуги, на которую он опирается.
\(\blacktriangleright\) Таким образом, если центральный угол \(\alpha_{\text{ц}}\) и вписанный угол \(\alpha_{\text{в}}\) опираются на одну и ту же дугу, то: \[\Large{\alpha_{\text{ц}}=2\cdot
\alpha_{\text{в}}}\]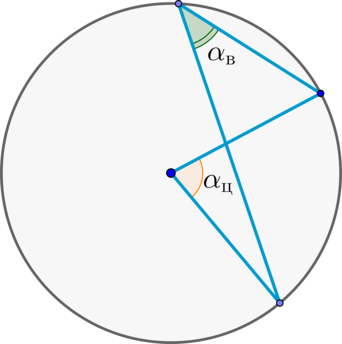
\(\blacktriangleright\) Вписанный угол, опирающийся на полуокружность (или на диаметр), равен \(90^\circ\).
Точки \(A\) и \(B\) делят окружность на две дуги, одна из которых равна \(170^\circ\), а другая точкой \(K\) делится в отношении \(11:8\), считая от точки \(A\). Найдите \(\angle BAK\). Ответ дайте в градусах.
Рассмотрим картинку: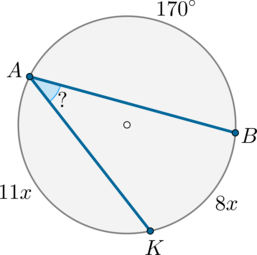
Т.к. \(\buildrel\smile\over{AK}:\buildrel\smile\over{KB}=11:8\), то можно обозначить \(\buildrel\smile\over{AK}=11x, \buildrel\smile\over{KB}=8x\).
Дуга \(\buildrel\smile\over{AKB}=360^\circ -170^\circ=190^\circ\). Следовательно, \(11x+8x=19x=190^\circ \quad \Rightarrow \quad x=10^\circ\). Значит, дуга \(\buildrel\smile\over{KB}=8x=80^\circ\). Угол \(BAK\) вписанный и опирается на эту дугу, следовательно, он равен ее половине, то есть \(40^\circ\).
Хорды \(KN\) и \(LM\) взаимно перпендикулярны. Найдите угол \(NLM\), если угол \(KML\) равен \(35^\circ\). Ответ дайте в градусах.
Рассмотрим картинку: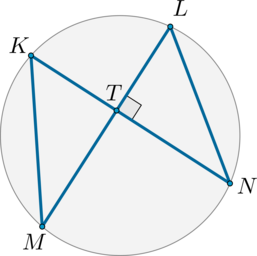
Вписанные углы \(KML\) и \(KNL\) опираются на одну и ту же дугу, следовательно, они равны, значит, \(\angle KNL=35^\circ\). Тогда \(\angle NLM=180^\circ-90^\circ-35^\circ=55^\circ\).
Точки \(A\) и \(C\) разбивают окружность на две дуги, одна из которых равна \(280^\circ\) и на которой отмечена точка \(B\). Найдите угол \(BAC\), если \(AB=AC\). Ответ дайте в градусах.
Рассмотрим картинку: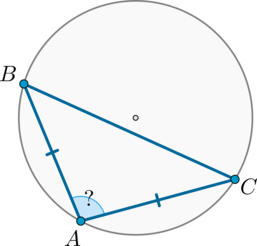
\(\buildrel\smile\over{ABC}=280^\circ\), следовательно, меньшая дуга \(\buildrel\smile\over{AC}=360^\circ-280^\circ=80^\circ\). Т.к. угол \(ABC\) опирается на эту дугу и является вписанным, то он равен ее половине, то есть \(40^\circ\).
Заметим, что \(\triangle ABC\) – равнобедренный, следовательно, \(\angle BAC=180^\circ-2\cdot 40^\circ=100^\circ\).
Точки \(A\), \(B\), \(C\) и \(D\) лежат на окружности с центром в точке \(O\) (так, что \(ABCD\) – четырёхугольник). Длина дуги \(AD\) (которая меньше полуокружности) составляет \(0,8\) длины дуги \(AB\) (которая меньше полуокружности). Найдите, во сколько раз \(\angle AOB\) больше, чем \(\angle DCA\).
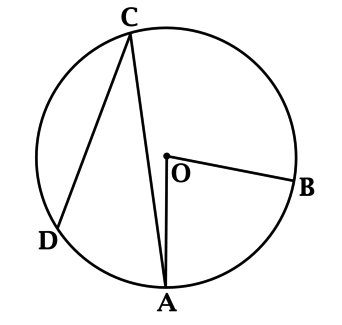
Градусные меры дуг окружности относятся как их длины, тогда градусная мера дуги \(AB\) в \(1: 0,8 = 1,25\) раз больше, чем градусная мера дуги \(AD\).
Градусной мерой дуги называется градусная мера центрального угла, который на неё опирается.
Вписанный угол равен половине градусной меры дуги, на которую он опирается, тогда \[\dfrac{\angle AOB}{\angle DCA} = \dfrac{\smile AB}{0,5 \smile AD} = 2 \cdot \dfrac{\smile AB}{\smile AD} = 2,5.\]
Хорды окружности \(AB\) и \(CD\) пересекаются в точке \(E\), причём \(CE = AE\). Градусная мера дуги \(AC\) равна \(120^{\circ}\), градусная мера дуги \(CAD\) равна \(210^{\circ}\). Найдите градусную меру дуги \(BD\). Ответ дайте в градусах.
Градусная мера дуги \(DA\) равна \(210^{\circ} - 120^{\circ} = 90^{\circ}\).
Соединим \(CA\).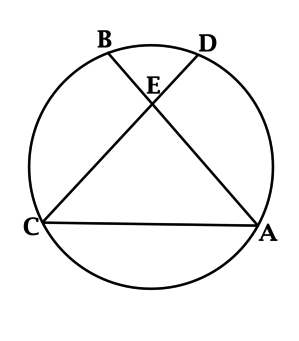
Треугольник \(AEC\) – равнобедренный, тогда \(\angle DCA = \angle BAC\), тогда дуги, на которые опираются эти вписанные углы, равны, следовательно градусная мера дуги \(BC\) равна \(90^{\circ}\).
Градусная мера дуги \(BD\) равна \(360^{\circ} - 120^{\circ} - 90^{\circ} - 90^{\circ} = 60^{\circ}\).
Четырехугольник \(ABCD\) вписан в окружность. Угол \(ABD\) равен \(75^\circ\), угол \(CAD\) равен \(35^\circ\). Найдите угол \(ABC\). Ответ дайте в градусах.
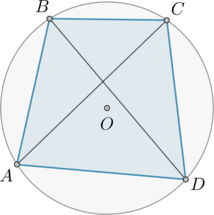
Так как вписанный угол равен половине дуги, на которую он опирается, то меньшая \(\buildrel\smile\over{DA}\,=2\cdot 75^\circ=150^\circ\) (см.рис.). Аналогично меньшая дуга \(\buildrel\smile\over{CD}\,=2\cdot 35^\circ=70^\circ\) (см.рис.). Следовательно, дуга \(\buildrel\smile\over{CDA}\,=150^\circ+70^\circ=220^\circ\). Значит \(\angle ABC\), как вписанный и опирающийся на дугу, равную \(220^\circ\), сам равен \(110^\circ\).
Чему равен тупой вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.

Обозначим хорду за \(AB\). Рассмотрим \(\triangle AOB\), где \(O\) – центр окружности.
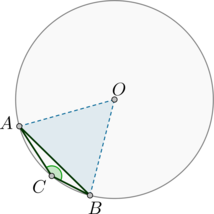
Так как \(AB\) равна радиусу окружности, то \(\triangle AOB\) – равносторонний. Следовательно, \(\angle AOB=60^\circ\).
Следовательно, меньшая дуга \(AB\) окружности равна \(\angle
AOB=60^\circ\). Тогда большая дуга \(AB\) окружности равна \(360^\circ-60^\circ=300^\circ\). Заметим, что \(\angle ACB\) – вписанный угол, опирающийся на большую дугу \(AB\), следовательно, он равен ее половине, то есть \(\angle ACB=150^\circ\).
Чаще всего процесс подготовки к ЕГЭ по математике начинается с повторения основных определений, формул и теорем, в том числе и по теме «Центральный и вписанный в окружность угол». Как правило, данный раздел планиметрии изучается еще в средней школе. Неудивительно, что многие учащиеся сталкиваются с необходимостью повторения базовых понятий и теорем по теме «Центральный угол окружности». Разобравшись с алгоритмом решения подобных задач, школьники смогут рассчитывать на получение конкурентных баллов по итогам сдачи единого госэкзамена.
Как легко и эффективно подготовиться к прохождению аттестационного испытания?
Занимаясь перед сдачей единого государственного экзамена, многие старшеклассники сталкиваются с проблемой поиска нужной информации по теме «Центральный и вписанный углы в окружности». Далеко не всегда школьный учебник имеется под рукой. А поиск формул в Интернете порой отнимает очень много времени.
«Прокачать» навыки и улучшить знания в таком непростом разделе геометрии, как планиметрия, вам поможет наш образовательный портал. «Школково» предлагает старшеклассникам и их преподавателям по-новому выстроить процесс подготовки к сдаче единого госэкзамена. Весь базовый материал представлен нашими специалистами в максимально доступной форме. Ознакомившись с информацией в разделе «Теоретическая справка», учащиеся узнают, какими свойствами обладает центральный угол окружности, как найти его величину и т. д.
Затем для закрепления полученных знаний и отработки навыков мы рекомендуем выполнить соответствующие упражнения. Большая подборка заданий на нахождение величины угла, вписанного в окружность, внешних углов многоугольника и других параметров представлена в разделе «Каталог». Для каждого упражнения наши специалисты прописали подробный ход решения и указали правильный ответ. Перечень задач на сайте постоянно дополняется и обновляется.
Готовиться к ЕГЭ, практикуясь в выполнении упражнений, к примеру, на нахождение величины центрального угла и длины дуги окружности, старшеклассники могут в онлайн-режиме, находясь в любом российском регионе.
При необходимости выполненное задание можно сохранить в разделе «Избранное», чтобы в дальнейшем вернуться к нему и еще раз разобрать принцип его решения.



