Введение в координатную плоскость

\(\blacktriangleright\) В прямоугольной системе координат \(Oxy\) даны точки \(A_1(x_1;y_1)\) и \(A_2(x_2;y_2)\). Тогда длина отрезка \(A_1A_2\) равна:
\[\Large{A_1A_2=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}}\]
\(\blacktriangleright\) В прямоугольной система координат даны точки \(A_1(x_1;y_1)\) и \(A_2(x_2;y_2)\).
Если \(O\) – середина отрезка \(A_1A_2\), то:
\[\Large{O\left(\dfrac{x_1+x_2}{2};\dfrac{y_1+y_2}{2}\right)}\]
Найдите площадь прямоугольника, вершины которого имеют координаты \((2;-1), \ (6;-1), \ (2;4), \ (6;4).\)
Назовем вершины прямоугольника: \(A(2;-1), \ B(6;-1), \ D(2;4), \
C(6;4)\).
Тогда длина отрезка \(AB\) – модуль разности абсцисс точек \(A\) и \(B\), длина отрезка \(AD\) – модуль разности ординат точек \(A\) и \(D\): \[AB=|6-2|=4, \quad AD=|4-(-1)|=5.\] Следовательно, площадь прямоугольника равна \[S=4\cdot 5=20.\]
Найдите площадь трапеции, вершины которой имеют координаты \((-1;-1),
\ (-1;2), \ (5;4), \ (5;0).\)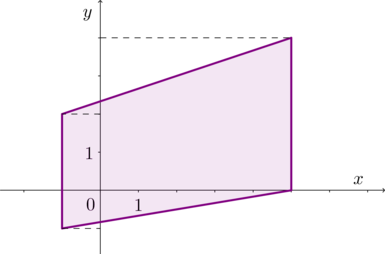
Назовем трапецию \(ABCD\), как показано на рисунке.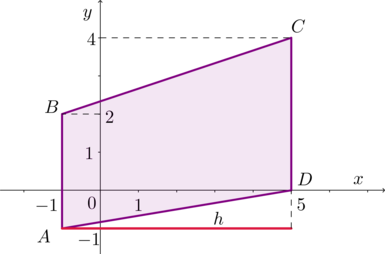
Тогда \(AB\) и \(CD\) – ее основания. \[AB=2-(-1)=3, \quad CD=4-0=4.\] Высота, опущенная из \(A\) на прямую \(CD\), равна \[h=5-(-1)=6.\] Следовательно, площадь: \[S=\dfrac12\cdot h\cdot (AB+CD)=\dfrac12\cdot 6\cdot (3+4)=21.\]
Найдите площадь треугольника, координаты которого имеют вершины \((1;12), (7;14), (7;20).\)
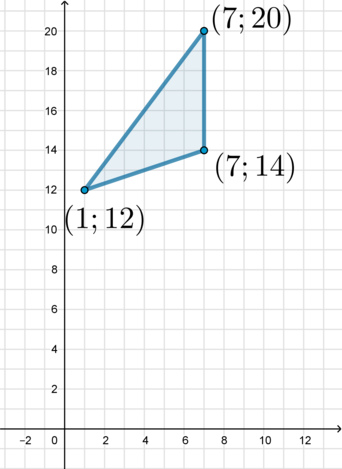
Площадь треугольника равна полупроизведению высоты на основание, у которому она проведена. Возьмем за основание отрезок с вершинами \((7;14)\) и \((7;20)\). Его длина равна \(6\). Высота к нему равна \(6\). Следовательно, \[S=\dfrac12\cdot 6\cdot 6=18\]
Найдите площадь параллелограмма, изображенного на рисунке.

Площадь параллелограмма равна произведению основания на высоту, проведенную к нему. У этого параллелограмма нижнее основание равно \(2\), а высота к нему равна \(3\). Следовательно, \[S=2\cdot 3=6\]
Найдите площадь трапеции, изображенной на рисунке.

Площадь трапеции равна полупроизведению суммы оснований на высоту. Основания этой трапеции равны \(2\) и \(4\). Высота равна \(5\). Следовательно, \[S=\dfrac{2+4}2\cdot 5=15\]
Найдите площадь трапеции, изображенной на рисунке.

Площадь трапеции равна полупроизведению суммы оснований на высоту. Основания этой трапеции равны \(2\) и \(8\). Высота равна \(3\). Следовательно, \[S=\dfrac{2+8}2\cdot 3=15\]
Найдите площадь треугольника, вершины которого имеют координаты \((1;1), \ (3;4), \ (6;2).\)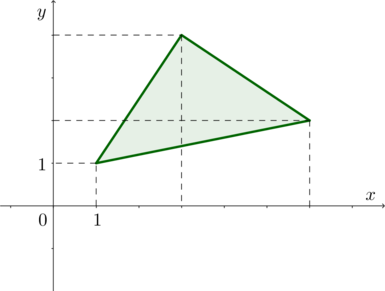
Обозначим вершины треугольника за \(A, B, C\) как показано на рисунке:
Тогда \[AC^2=(3-1)^2+(4-1)^2=13, \quad BC^2=(6-3)^2+(4-2)^2=13.\] Следовательно, треугольник равнобедренный. Найдем его высоту, опущенную из \(C\).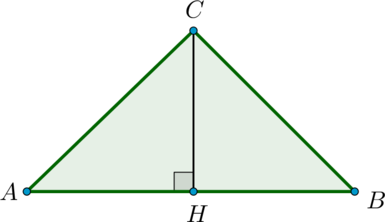
\(AB=\sqrt{(6-1)^2+(2-1)^2}=\sqrt{26}\), следовательно, \(AH=\frac{\sqrt{26}}2\). Тогда: \[CH^2=\sqrt{AC^2-AH^2}=\sqrt{\dfrac{13}2}\] Значит, площадь равна \[S=\dfrac 12\cdot AB\cdot CH=\dfrac{13}2=6,5.\]
Задачи на координатной плоскости, в которых требуется выполнить построения, являются обязательной частью ЕГЭ по математике. Знать алгоритм их решения должны ученики, которые готовятся сдавать базовый и профильный уровень экзамена. Поняв, как решаются задачи по теме «Координатная плоскость», выпускники смогут успешно справляться с заданиями с различным количеством действий и рассчитывать на получение конкурентных баллов по итогам сдачи ЕГЭ.
Как подготовиться к экзамену?
На этапе подготовки к аттестационному испытанию многие учащиеся сталкиваются со сложностью поиска подходящего источника. В нужный момент школьного учебника может просто не оказаться под рукой. А найти необходимые определения и теоремы иногда бывает достаточно сложно даже в Интернете.
Вместе с образовательным порталом «Школково» вы сможете качественно подготовиться к сдаче ЕГЭ. Наш ресурс выстроен таким образом, чтобы учащиеся имели возможность выявить наиболее сложные для себя разделы и восполнить пробелы в знаниях.
В соответствующем разделе сайта представлен весь базовый теоретический материал по теме «Координатная плоскость», который поможет в подготовке к ЕГЭ. Данная информация, как и решение задач по теореме синусов и косинусов, систематизирована и изложена нашими специалистами с учетом их богатого опыта в максимально доступной форме.
Чтобы закрепить полученные знания по теме «Координатная плоскость», рекомендуем школьникам также попрактиковаться в решении задач. Большая подборка упражнений представлена в разделе «Каталог». Для каждого задания наши специалисты прописали подробный алгоритм решения и указали правильный ответ. Перечень упражнений в соответствующем разделе постоянно дополняется и обновляется.
Тренироваться решать задачи на координатной плоскости школьники могут в режиме онлайн, находясь в Московском регионе или других российских областях. При необходимости любое упражнение можно сохранить в «Избранное». Это позволит в дальнейшем без труда вернуться к этой задаче и, к примеру, обсудить алгоритм ее решения со своим преподавателем.



