Сюжетные текстовые задачи

Катер движется по стоячей воде. Собственная скорость катера - \(35\) км/ч. Навстречу катеру дует ветер, который за каждый час сносит катер на \(3\) км назад. За сколько часов катер доберется в назначенный пункт, если он находится на расстоянии \(144\) км от места начала движения катера?
Так как за час катер проходил бы 35 км, но ветер сносит его назад на 3 км, то в итоге за час катер проходит 32 км. Следовательно, 144 км катер пройдет за \(144:32=4,5\) часа.
Яхта движется по стоячей воде, ее собственная скорость - \(30\) км/ч, встречный ветер каждую минуту сносит яхту на \(20\) метров. За сколько часов яхта пройдет \(259\,200\) метров?
За каждый час яхта проходила бы 30 км, или 30000 метров, значит, за минуту она проходила бы \(30\,000:60=500\) метров. Так как за каждую минуту ветер сносит ее на 20 метров, то в итоге за минуту яхта проходит 480 метров. Следовательно, ей понадобится \(259\,200:480=540\) минут или \(540:60=9\) часов.
Два велосипедиста выехали из одного места в одном направлении. Скорость первого – 10 км/ч, а второго – 18 км/ч. Через сколько часов расстояние между велосипедистами будет равно 104 км?

Заметим, что за каждый час второй велосипедист будет проходить на \(18-10=8\) км больше, чем первый. Следовательно, 8 км/ч – скорость удаления. Изначально между велосипедистами было расстояние 0 км, стало – 104 км, следовательно, расстояние между ними изменилось на 104 км. Значит, прошло \(104:8=13\) часов.
Два велосипедиста выехали в одном направлении из мест, находящихся на расстоянии 13 км друг от друга. Скорость первого – 12 км/ч, а второго – 17 км/ч, причем второй находился в начале движения впереди. Через сколько часов расстояние между велосипедистами будет равно 58 км?
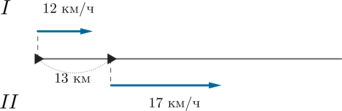
Заметим, что за каждый час второй велосипедист будет проходить на \(17-12=5\) км больше, чем первый. Следовательно, 5 км/ч – скорость удаления. Изначально между велосипедистами было расстояние 13 км, стало – 58 км, следовательно, расстояние между ними изменилось на \(58-13=45\) км. Значит, прошло \(45:5=9\) часов.
Альпинистка Маша начала ползти по стене, находясь на высоте \(2,75\) м от пола. За каждую минуту она поднималась бы на \(1,5\) м, но ветер тут же сносит ее вниз на \(0,25\) м. Сколько минут она ползет, если теперь она находится на высоте \(14\) м от пола?
Так как Маша уже находилась на высоте 2,75 м, то проползла она за время наблюдения \(14-2,75=11,25\) метров. Заметим, что в итоге за каждую минуту она поднимается на 1,25 метров. Следовательно, время, которое она затратила на подъем, равно \[11,25:1,25=9 \ {\small{\text{минут.}}}\]
Два туриста одновременно вышли в одном направлении в город N. При этом вышли они из разных городов, расстояние между которыми 9 км. Известно, что турист, изначально находившийся дальше от города N, шёл со скоростью, в два раза превышающей скорость другого туриста. В город N они прибыли одновременно, через 3 часа после начала движения. Найдите скорость туриста, который шёл быстрее. Ответ дайте в км/ч.
Пусть \(v\) км/ч – скорость медленного туриста.
Тогда расстояние, которое прошёл медленный турист, равно \(3v\), а расстояние, которое прошёл быстрый турист, равно \(2v \cdot 3 = 6v\).
Так как быстрый турист прошёл на 9 км больше, то:
\[6v - 3v = 9,\] откуда находим \(v = 3\) км/ч, значит скорость быстрого туриста \(2\cdot 3 = 6\) км/ч.
Лыжник планировал проехать \(4\, км\) с горы с постоянной скоростью \(v\). Вместо этого первые два километра он проехал в два раза быстрее, чем планировал, а оставшиеся два километра он проехал в два раза медленнее, чем планировал. Во сколько раз больше времени ушло у лыжника на самом деле, чем должно было бы уйти, если бы всё в его жизни было по плану?
Пусть по плану на весь маршрут лыжника должно было уйти \(t\) часов, тогда на первые два километра (которые составляют половину пути) у лыжника ушло \[t\cdot\dfrac{1}{2}\cdot\dfrac{1}{2} = 0,25t\, ч\,,\] а на оставшиеся два километра ушло \[t\cdot\dfrac{1}{2}\cdot 2 = t\, ч\,,\] следовательно, на весь путь ушло \(1,25t\, ч\), то есть в \(1,25\) раза больше, чем было запланировано изначально.



