Угловой коэффициент касательной как значение производной в точке касания

Если \(y=kx+b\) — уравнение касательной к кривой \(f(x)\), то
\[{\large{k=f'(x_o),}}\] где \(x_o\) — абсцисса точки касания прямой и кривой.
Прямая \(y=12x+13\) является касательной к графику функции \(y=x^3-9x^2-9x+2\). Найдите абсциссу точки касания.
Пусть \(x_0\) – точка касания. Так как значение производной в точке касания равно угловому коэффициенту касательной и \(y'=3x^2-18x-9\), то \[3x_0^2-18x_0-9=12 \quad \Leftrightarrow\quad x_0=7 \quad {\small{\text{и}}}\quad x_0=-1.\] Так как \(y=12x+13\) и \(y=x^3-9x^2-9x+2\) имеют общую точку (и это точка касания), то \[12x_0+13=x_0^3-9x_0^2-9x_0+2\] Проверим значение \(x_0=-1\): \[12\cdot (-1)+13=(-1)^3-9\cdot (-1)^2-9\cdot (-1)+2 \quad \Leftrightarrow\quad 0=0\] Аналогичной проверкой убеждаемся, что \(x_0=7\) не подходит. Следовательно, ответ \(-1.\)
Прямая \(y=12x-73\) является касательной к графику функции \(y=ax^2-18x+2\). Найдите \(a\).
Пусть \(x_0\) – точка касания. Так как значение производной в точке касания равно угловому коэффициенту касательной и \(y'=2ax-18\), то \[2ax_0-18=12 \quad \Leftrightarrow\quad x_0=\dfrac{15}a\quad (1)\] Так как \(y=12x-73\) и \(y=ax^2-18x+2\) имеют общую точку (и это точка касания), то \[12x_0-73=ax_0^2-18x_0+2\quad (2)\] Подставим \((1)\) в \((2)\): \[\dfrac{15^2}a-\dfrac{30\cdot 15}a+75=0 \ \Bigg|:75\quad \Leftrightarrow \quad -\dfrac3a+1=0 \quad\Leftrightarrow\quad a=3.\]
Прямая \(y=8(2x-1)\) параллельна касательной к графику функции \(f(x)=3x^2+7x+5\). Найдите абсциссу точки касания.
Так как параллельные прямые имеют равные угловые коэффициенты, то уравнение касательной будет выглядеть так: \(y_k=16x+b\), где \(b\) – некоторое число.
Так как значение производной в точке касания равно угловому коэффициенту касательной, то, если \(x_0\) – абсцисса точки касания, \[f'(x_0)=16 \quad\Rightarrow\quad 6x_0+7=16 \quad\Leftrightarrow\quad
x_0=\dfrac32=1,5.\]
Прямая \(y=7x-5\) параллельна касательной к графику функции \(y=x^2+6x-8\). Найдите абсциссу точки касания.
Пусть \(y_k=kx+b\) – уравнение касательной. Так как \(y=7x-5\) параллельна \(y_k\), то их угловые коэффициенты равны, следовательно, \(k=7\).
Так как угловой коэффициент касательной к графику функции \(f(x)\) равен значению производной функции в точке касания \(x_0\), то есть \(7=k=f'(x_0)\), а \(f'(x)=2x+6\), то \[7=2x_0+6\quad\Leftrightarrow\quad x_0=0,5\]
Прямая, заданная уравнением \(y = 3x + 1\), касается графика функции \(f(x)\) в точке \((x_0; f(x_0))\). Найдите \(f'(x_0)\).
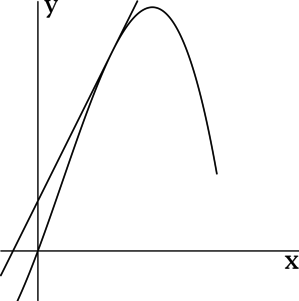
Производная функции \(f(x)\) в точке \(x_0\) равна угловому коэффициенту \(a\) касательной \(y = ax + b\) в точке \((x_0; f(x_0))\).
Таким образом, \(f'(x_0) = 3\).
Прямая, заданная уравнением \(y = -x - 1\), касается графика функции \(f(x)\) в точке \((x_0; f(x_0))\). Найдите \(f'(x_0)\).
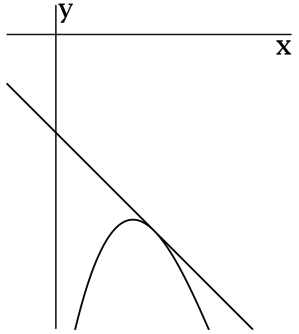
Производная функции \(f(x)\) в точке \(x_0\) равна угловому коэффициенту \(a\) касательной \(y = ax + b\) в точке \((x_0; f(x_0))\).
Таким образом, \(f'(x_0) = -1\).
Прямая, заданная уравнением \(y = 1,5x\), касается графика функции \(f(x)\) в точке \((x_0; f(x_0))\). Найдите \(f'(x_0)\).
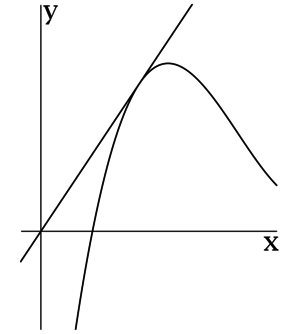
Производная функции \(f(x)\) в точке \(x_0\) равна угловому коэффициенту \(a\) касательной \(y = ax + b\) в точке \((x_0; f(x_0))\).
Таким образом, \(f'(x_0) = 1,5\).
Задачи на нахождение производной касательной включены в ЕГЭ по математике и встречаются там ежегодно. При этом статистика последних лет показывает, что подобные задания вызывают у выпускников определенные затруднения. Поэтому, если учащийся рассчитывает получить достойные баллы по итогам прохождения ЕГЭ, то ему непременно стоит научиться справляться с задачами из раздела «Угловой коэффициент касательной как значение производной в точке касания», подготовленными специалистами образовательного портала «Школково». Разобравшись с алгоритмом их решения, ученик сможет успешно преодолеть аттестационное испытание.
Основные моменты
Приступая к решению задач ЕГЭ по данной теме, необходимо вспомнить основное определение: производная функции в точке равна угловому коэффициенту касательной к графику функции в этой точке. В этом и состоит геометрический смысл производной.
Необходимо освежить в памяти и другое важное определение. Оно звучит следующим образом: угловой коэффициент равняется тангенсу угла наклона касательной к оси абсцисс.
Какие еще важные моменты стоит отметить в этой теме? При решении задач на нахождение производной в ЕГЭ необходимо помнить, что угол, который образует касательная, может быть меньше, больше 90 градусов или равняться нулю.
Как подготовиться к экзамену?
Для того, чтобы задания в ЕГЭ на тему «Угловой коэффициент касательной как значение производной в точке касания» давались вам достаточно легко, воспользуйтесь при подготовке к выпускному испытанию информацией по этому разделу на образовательном портале «Школково». Здесь вы найдете необходимый теоретический материал, собранный и понятно изложенный нашими специалистами, а также сможете попрактиковаться в выполнении упражнений.
Для каждого задания, например, задач на тему «Угловой коэффициент касательной как тангенс угла наклона», мы прописали правильный ответ и алгоритм решения. При этом учащиеся могут выполнять упражнения различного уровня сложности в режиме онлайн. В случае необходимости задачу можно сохранить в разделе «Избранное», чтобы потом обсудить ее решение с преподавателем.



