Задачи с окружностями (страница 2)

\(\blacktriangleright\) Радикальная ось — прямая, проходящая через точки пересечения двух окружностей.
Линия центров окружностей — прямая, проходящая через центры двух окружностей.
Радикальная ось перпендикулярна линии центров окружностей. Отрезки касательных, проведенных из любой точки радикальной оси к этим окружностям, равны.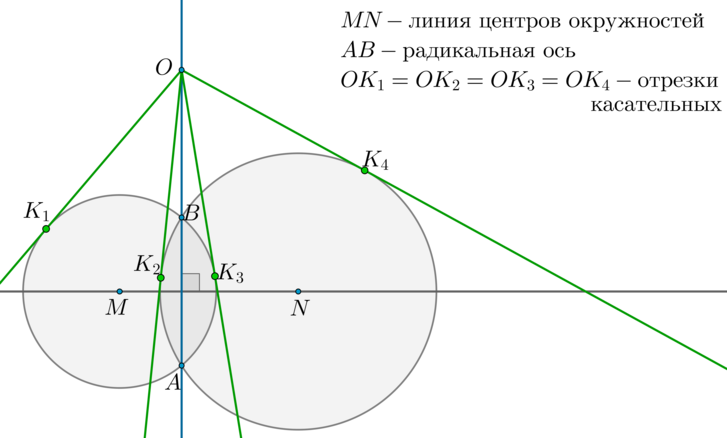
\(\blacktriangleright\) Пусть две окружности с центрами \(M\) и \(N\) касаются внешним образом в точке \(A\). Две общие касательные (внутренняя и внешняя) \(a\) и \(b\) этих окружностей пересекаются в точке \(B\). Точки касания — точки \(A, K_1, K_2\). Тогда \[{\large{K_1B=AB=K_2B}}\] \[{\large{\angle K_1AK_2=90^\circ}}\]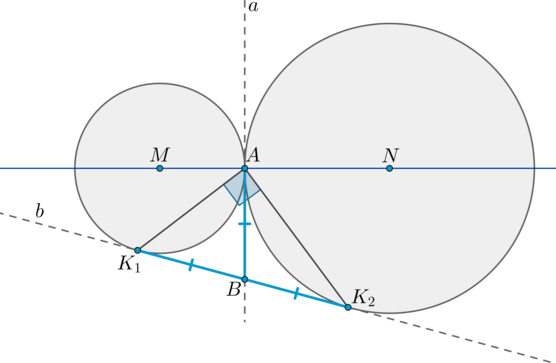
\(\blacktriangleright\) Пусть две окружности касаются внешним образом в точке \(A\). Через точку \(A\) проведены две прямые \(B_1B_2\) и \(C_1C_2\), пересекающие каждую окружность в двух точках, как показано на рисунке. Тогда: \[{\large{\triangle AB_1C_1 \sim \triangle
AB_2C_2}}\] \[{\large{B_1C_1\parallel B_2C_2}}\]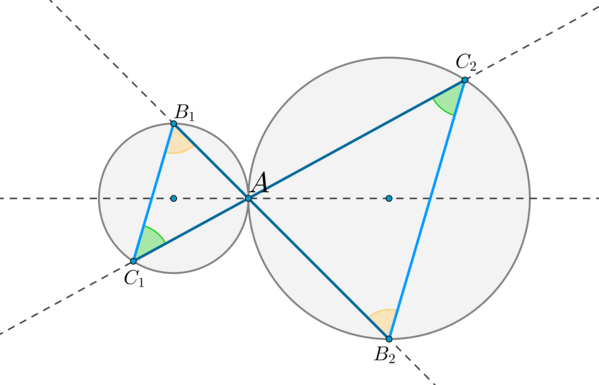
\(\blacktriangleright\) Формула Эйлера: Пусть \(R\) — радиус описанной около треугольника окружности, \(r\) — радиус вписанной окружности. Тогда расстояние между центрами этих окружностей вычисляется по формуле: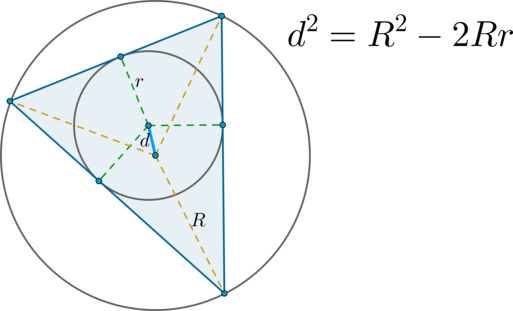
\(\blacktriangleright\) Теорема о бабочке: Пусть через середину хорды \(AB\) — точку \(O\), проведены две хорды \(MN\) и \(KP\). Пусть \(MP\cap AB=X, KN\cap AB=Y\). Тогда \[{\large{OX=OY}}\]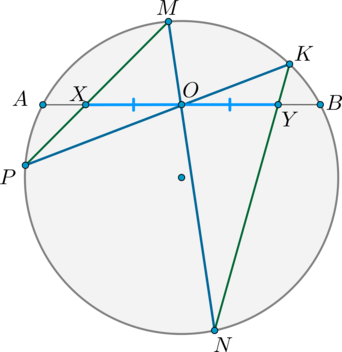
Окружность касается стороны \(BC=15\) и продолжений сторон \(AB=AC=8,5\) треугольника \(ABC\). Найдите радиус этой окружности.
Заметим, что треугольник \(ABC\) равнобедренный. Т.к. центр окружности равноудален от сторон угла \(A\), то он лежит на биссектрисе этого угла (то есть \(AO\) – биссектриса \(\angle A\)). Т.к. треугольник равнобедренный, то биссектриса \(AO\) является также медианой и высотой, следовательно, т.к. \(OM\perp BC\) (\(M\) – точка касания), то точка \(M\) лежит на отрезке \(AO\).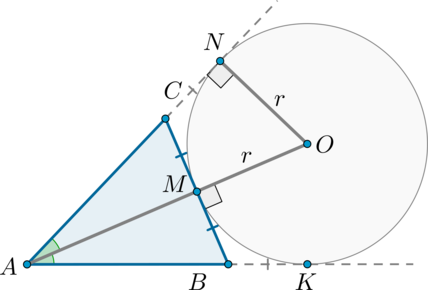
\(\triangle ACM\sim \triangle ANO\) по двум углам. Следовательно,
\[\dfrac{CM}{ON}=\dfrac{AC}{AO} \quad \Rightarrow \quad \dfrac{\frac{15}2}r=\dfrac{8,5}{AM+r}\]
Таким образом, для того, чтобы найти \(r\), нужно сначала найти \(AM\).
По теореме Пифагора из \(\triangle AMC\): \(AM^2=AC^2-MC^2=8,5^2-7,5^2=16\), следовательно, \(AM=4\). Значит:
\[\dfrac{\frac{15}2}{r}=\dfrac{8,5}{4+r} \quad \Rightarrow \quad r=30.\]
Окружность касается стороны \(AB\) и продолжения сторон \(BC\) и \(AC\) треугольника \(ABC\), причем \(AB=AC=17\), \(BC=30\). Найдите радиус этой окружности.
Т.к. окружность вписана в угол \(BAK\), то ее центр лежит на его биссектрисе, следовательно, \(AO\) – биссектриса \(\angle BAK\). Обозначим \(\angle BAO=\angle KAO=\alpha\). Тогда \(\angle
BAC=180^\circ-2\alpha\). Т.к. \(\triangle ABC\) – равнобедренный, то с другой стороны \(\angle BAC=180^\circ-2\angle B=180^\circ-2\angle C\). Таким образом, \(\angle B=\angle C=\alpha\).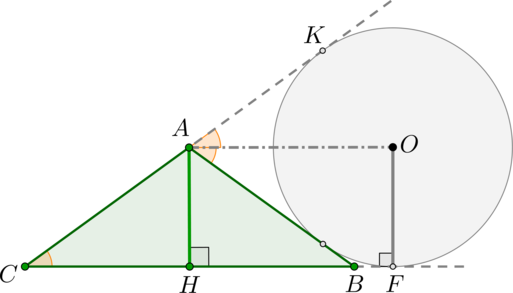
Следовательно, \(\angle ACB=\angle KAO\) как соответственные при прямых \(CB\) и \(AO\) и секущей \(CA\). Следовательно, по признаку \(CB\parallel AO\).
Проведем \(AH\perp BC\). Т.к. \(\triangle ABC\) – равнобедренный, то \(AH\) – медиана.
Имеем: \(AH=OF\) как отрезки перпендикулярных прямых, заключенные между параллельными прямыми \(BC\) и \(AO\). А \(AH\) можно найти по теореме Пифагора из \(\triangle AHB\):
\[AH^2=AB^2-HB^2=17^2-15^2=8^2 \quad \Rightarrow \quad r=OF=AH=8.\]
В треугольнике со сторонами \(a,b,c\) радиус вписанной окружности равен \(r=\frac{a+b-c}2\). Докажите, что треугольник является прямоугольным.
Как известно, площадь треугольника равна произведению его полупериметра на радиус вписанной окружности. С другой стороны, площадь можно найти по формуле Герона. Следовательно:
\[S=\sqrt{p(p-a)(p-b)(p-c)}=p\cdot r \quad \Rightarrow \quad (p-a)(p-b)(p-c)=p\cdot r^2\]
Т.к. \(p=\dfrac{a+b+c}2\), \(r=\dfrac{a+b-c}2\), то
\(\dfrac{a+b-c}2\cdot \dfrac{a+c-b}2\cdot \dfrac{b+c-a}2=\dfrac{a+b+c}2\cdot \dfrac{(a+b-c)^2}4 \quad \Rightarrow \)
\(\Rightarrow \quad (c+(a-b))(c-(a-b))=((a+b)+c)((a+b)-c) \quad \Rightarrow \quad c^2-(a-b)^2=(a+b)^2-c^2\)
\(\Rightarrow \quad c^2-a^2+2ab-b^2=a^2+2ab+b^2-c^2 \quad \Rightarrow \quad c^2=a^2+b^2\)
Таким образом, по обратной теореме Пифагора треугольник будет прямоугольным, причем прямой угол находится против стороны \(c\).
Доказательство
Четырехугольник \(ABCD\) вписан в окружность, причем \(\angle ACD=90^\circ\), \(\angle ACB=\angle BAD\), \(AD=2\), \(CD=\frac65\).
Найдите длину отрезка \(BC\).
1) Т.к. \(\angle ACD=90^\circ\), то он опирается на диаметр, то есть \(AD\) – диаметр. Следовательно, \(\angle ABD=90^\circ\).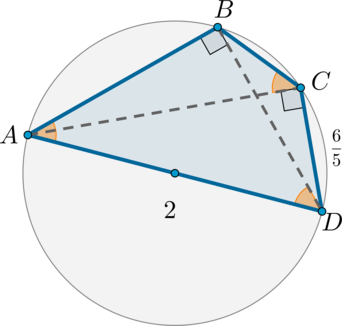
Вписанные углы \(\angle ACB\) и \(\angle ADB\) равны, т.к. опираются на одну и ту же дугу. Следовательно, \(\triangle ABD\) – прямоугольный и равнобедренный, то есть \(\angle BDA=\angle BAD=45^\circ\) и \(AB=BD=AD\div\sqrt2=\sqrt2\).
2) По теореме Пифагора из \(\triangle ACD\):
\[AC=\sqrt{AD^2-CD^2}=\sqrt{4-\frac{36}{25}}=\dfrac85\]
Тогда по теореме косинусов из \(\triangle ABC\):
\[AB^2=AC^2+BC^2-2\cdot AC\cdot BC\cdot \cos45^\circ \quad \Rightarrow \quad 2=\dfrac{64}{25}+BC^2-2\cdot \dfrac85\cdot BC\cdot \dfrac{\sqrt2}2\]
Решая полученное квадратное уравнение, находим, что \(BC=\dfrac{\sqrt2}5\) или \(BC=\dfrac{7\sqrt2}5\).
Заметим, что в \(\triangle ABC\) угол \(B\) – тупой, следовательно, против него должна лежать большая сторона. Таким образом, число \(\dfrac{7\sqrt2}5\) не подходит, т.к. \(\dfrac{7\sqrt2}5>\dfrac85=AC\).
Таким образом, \(BC=\dfrac{\sqrt2}5\).
\(\dfrac{\sqrt2}5\)
Найдите радиус окружности, проходящей через вершину \(C\) прямого угла треугольника \(ABC\), основание \(H\) высоты \(CH\) и точку \(K\) — середину катета \(BC\), если гипотенуза треугольника равна \(c\).
Сразу заметим, что \(\angle C=90^\circ\) — вписанный угол, следовательно, он опирается на диаметр. Значит, если \(M\) – точка пересечения окружности с катетом \(AC\), то \(MK\) – диаметр.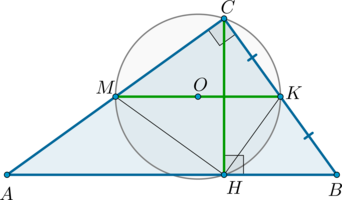
Заметим, что в \(\triangle CHB\) \(HK\) — медиана, проведенная из вершины прямого угла, следовательно, она равна половине гипотенузы, то есть \(HK=KC\).
Таким образом, прямоугольные треугольники \(MCK\) и \(MHK\) (\(\angle H=90^\circ\), т.к. опирается на диаметр) равны по катету и гипотенузе. Значит, \(KM\) – содержит биссектрису \(\angle
CKH\), а т.к. \(\triangle CKH\) равнобедренный, то и высоту, то есть \(KM\perp CH\).
По условию также \(CH\perp AB\), следовательно, \(MK\parallel AB\). Значит, по теореме Фалеса \(M\) – также середина катета \(AC\), то есть \(MK\) – средняя линия.
Значит, радиус окружности равен \[R=\dfrac12 MK=\dfrac12\cdot \dfrac12AB=\dfrac14c.\]
\(\dfrac c4\)
Окружности \(S_1\) и \(S_2\) пересекаются в точках \(A\) и \(B\), центр \(O\) окружности \(S_1\) лежит на окружности \(S_2\). Хорда \(AC\) окружности \(S_1\) пересекает окружность \(S_2\) в точке \(D\). Докажите, что отрезки \(OD\) и \(BC\) перпендикулярны.
Рассмотрим рисунок: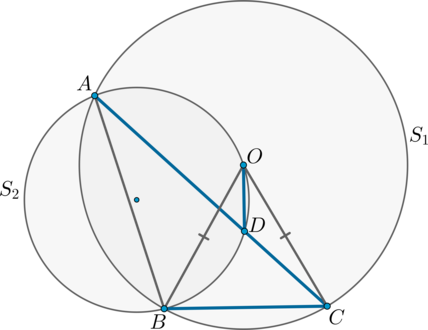
Проведем дополнительно \(OB, OC, AB\). Заметим, что \(\triangle BOC\) равнобедренный, следовательно, необходимо доказать, что прямая \(OD\) содержит высоту, опущенную к основанию. Докажем, что прямая \(OD\) содержит биссектрису, тогда отсюда будет следовать утверждение задачи.
Таким образом, необходимо доказать, что \(\angle BOD=\angle COD\).
Заметим, что \(\angle BOD=\angle BAD=\alpha\) как вписанные углы в окружности \(S_2\), опирающиеся на одну и ту же дугу \(\buildrel\smile\over{BD}\).
С другой стороны, \(\angle BAC\) (он же \(\angle BAD\)) — вписанный угол в окружности \(S_1\), опирающийся на дугу \(\buildrel\smile\over{BC}\), следовательно, \(\buildrel\smile\over{BC}=2\angle BAC=2\alpha\).
\(\angle BOC\) — центральный угол в окружности \(S_1\), опирающийся на дугу \(\buildrel\smile\over{BC}\), следовательно, \(\angle
BOC=\buildrel\smile\over{BC}=2\alpha\).
Отсюда \(\angle COD=\angle BOC-\angle BOD=2\alpha-\alpha=\alpha\). Следовательно, \(OD\) – часть биссектрисы равнобедренного треугольника \(BOC\), а следовательно, и часть высоты, чтд.
Доказательство
К двум окружностям, пересекающимся в точках \(M\) и \(K\), проведена общая касательная. Докажите, что если \(A\) и \(B\) – точки касания, то \(\angle AMB+\angle AKB=180^\circ\).
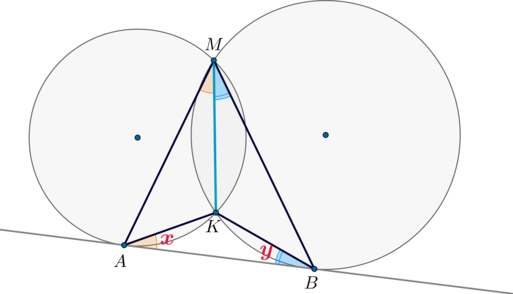
Обозначим за \(x\) угол \(KAB\), за \(y\) — угол \(KBA\). Т.к. это углы между касательной \(AB\) и хордами \(AK\) и \(BK\) соответственно, то каждый из них половине дуги, заключенной между касательной и соответствующей хордой, то есть
\[\begin{aligned} &x=\angle KAB=0,5\cdot\buildrel\smile\over{AK}\\ &y=\angle KBA=0,5\cdot\buildrel\smile\over{BK}\end{aligned}\]
Заметим, что \(\angle AMK\) – вписанный, опирающийся на \(\buildrel\smile\over{AK}\), следовательно, \(\angle AMK=x\). Аналогично \(\angle BMK=y\).
Таким образом, \(\angle AMB=x+y\).
Из \(\triangle AKB\): \[\angle AKB+x+y=180^\circ \quad \Rightarrow \quad \angle AKB+\angle AMB=180^\circ, \ \text{ чтд.}\]
Эта же задача с другим решением представлена в разделе “Задачи, требующие дополнительного построения”.
Доказательство



