Задачи на подобие треугольников и пропорциональные отрезки

\(\blacktriangleright\) Если на одной из сторон угла отметить равные между собой отрезки и через их концы провести параллельные прямые, то эти прямые отсекут на второй стороне также равные между собой отрезки.
\(\blacktriangleright\) Теорема Фалеса: параллельные прямые отсекают на сторонах угла пропорциональные отрезки.
Наиболее часто встречающиеся подобия треугольников:
\(\blacktriangleright\) Средняя линия треугольника отсекает от него подобный ему треугольник.
\(\blacktriangleright\) Треугольники, образованные диагоналями трапеции и основаниями, подобны.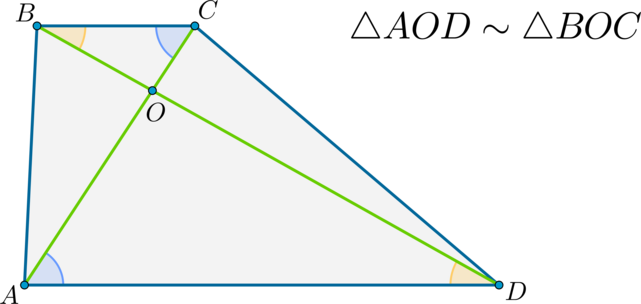
\(\blacktriangleright\) Высота прямоугольного треугольника, проведенная к гипотенузе, делит его на два подобных треугольника.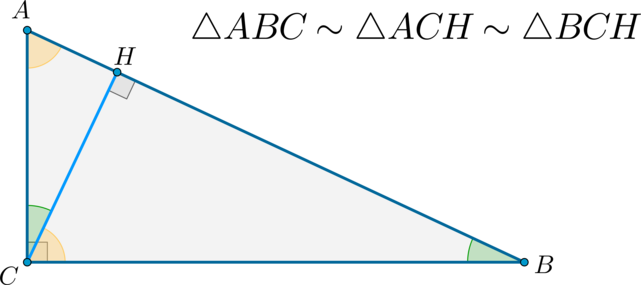
\(\blacktriangleright\) Отрезки, соединяющие основания высот треугольника, отсекают от него подобные ему треугольники.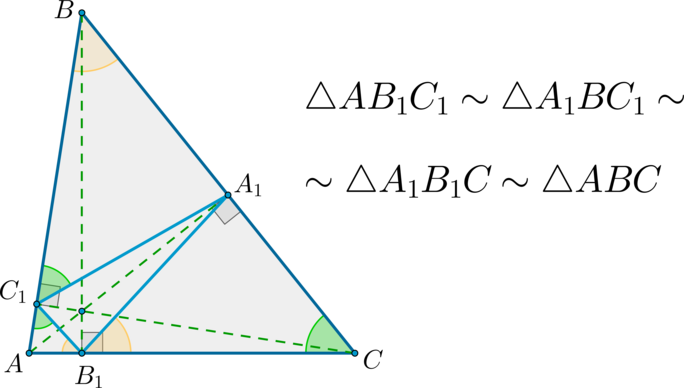
\(\blacktriangleright\) Если к окружности из одной точки вне окружности проведены две секущие, то: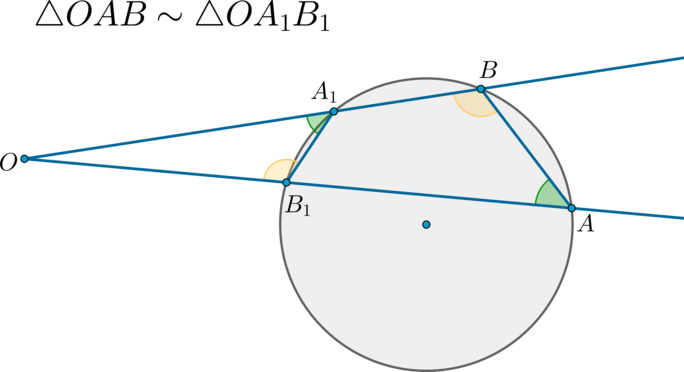
\(\blacktriangleright\) Если к окружности из одной точки проведены касательная и секущая, то: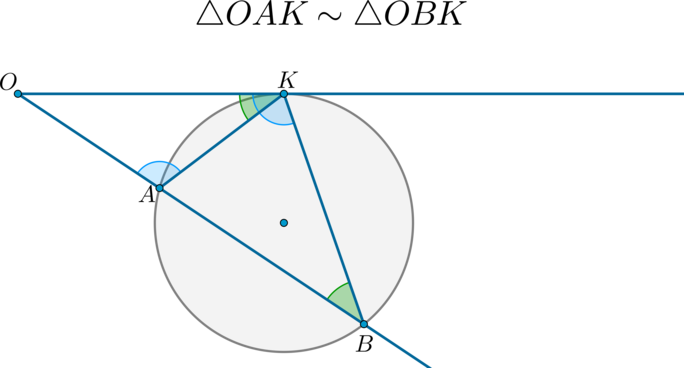
\(\blacktriangleright\) Если в окружности две хорды пересекаются, то: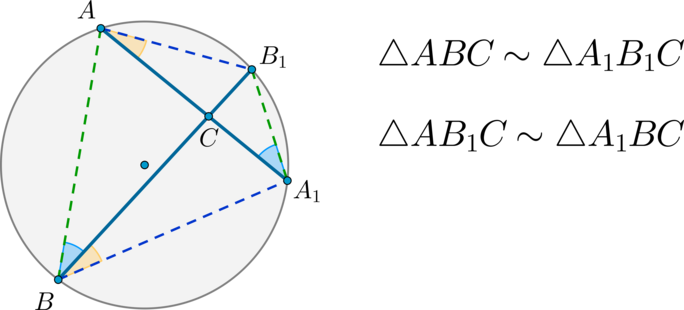
В квадрате \(ABCD\) на стороне \(CD=\sqrt{13}\) взята точка \(K\) такая, что \(DK=\frac23DC\). Найдите расстояние от точки \(B\) до прямой \(AK\).
Обозначим сторону квадрата за \(3x\), тогда \(DK=2x\), \(KC=x\). Необходимо найти \(BH\).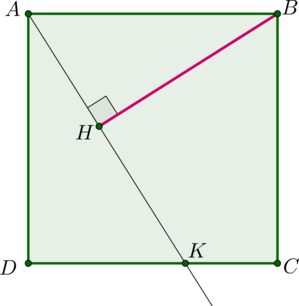
Заметим, что \(\triangle ADK\sim \triangle ABH\) по двум углам (\(\angle ADK=\angle AHB=90^\circ\), \(\angle AKD=\angle HAB\) как накрест лежащие). Следовательно, \[\dfrac{BH}{AD}=\dfrac{AB}{AK}.\] По теореме Пифагора \(AK=\sqrt{AD^2+DK^2}=\sqrt{13}x\), следовательно, \[BH=\dfrac{AD\cdot AB}{AK}=\dfrac{9x^2}{\sqrt{13}x}=\dfrac9{\sqrt{13}}x\] Так как \(AD=\sqrt{13}=3x\), то \(x=\frac{\sqrt{13}}3\), следовательно, \[BH=3.\]
Хорда \(AB=15\), хорда \(AC=21\), а хорда \(BC=24\). Точка \(D\) – середина дуги \(CB\). На какие части делится хорда \(BC\) прямой \(AD\)?
(Источник: Сборник задач по геометрии, И.Ф.Шарыгин, Р.К.Гордин)
Пусть \(E\) – точка пересечения \(AD\) и \(BC\).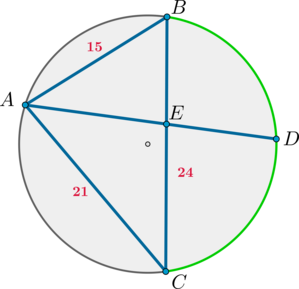
Так как углы \(CAD\) и \(BAD\) опираются на равные дуги и оба являются вписанными, то они равны. Следовательно, \(AD\) – биссектриса \(\angle
A\). Тогда в треугольнике \(ABC\) по свойству биссектрисы \[\dfrac{BE}{EC}=\dfrac{AB}{AC}=\dfrac{15}{21}=\dfrac57\] Можно обозначить \(BE=5x\), \(EC=7x\). Тогда \(5x+7x=24\), откуда \(x=2\). Следовательно, \(BE=10\), \(EC=14\).
10 и 14
В трапеции основания равны \(18\) и \(12\), а боковые стороны \(15\) и \(12\). Боковые стороны продолжили до взаимного пересечения. Найдите сумму длин отрезков, на которые продолжены боковые стороны.
Пусть дана трапеция \(ABCD\), \(AD, BC\) – основания, \(O\) – точка пересечения продолжений боковых сторон. Обозначим \(OB=x, OC=y\).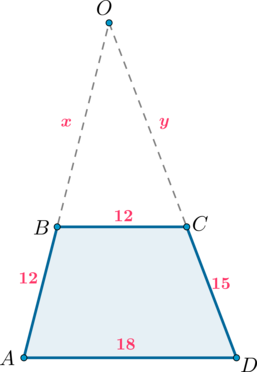
Тогда \(\triangle AOD\sim \triangle BOC\) по двум углам: \(\angle O\) – общий, \(\angle OBC=\angle OAD\) как соответственные при \(AD\parallel
BC\) и \(AO\) секущей. Следовательно: \[\dfrac{x}{x+12}=\dfrac{12}{18}=\dfrac{y}{y+15} \quad\Leftrightarrow\quad
x=24; \quad y=30; \quad\Leftrightarrow\quad x+y=24+30=54.\]
Окружность касается одного из катетов прямоугольного равнобедренного треугольника и проходит через вершину противолежащего острого угла. Найдите радиус окружности, если ее центр лежит на гипотенузе треугольника, а катет треугольника равен \(\sqrt2+1\).
(Источник: Сборник задач по геометрии, И.Ф.Шарыгин, Р.К.Гордин)
В решении будем обозначать катет треугольника за \(a\). Пусть \(r\) – радиус окружности. Если \(K\) – точка касания окружности с катетом \(BC\), то \(OK\perp BC\). Рассмотрим рисунок: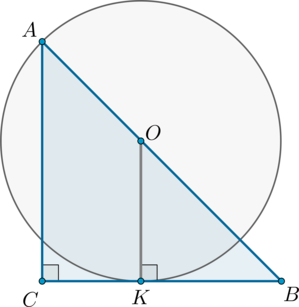
Заметим, что по двум углам \(\triangle BOK\sim \triangle BAC\), следовательно, \[\dfrac{OK}{AC}=\dfrac{BK}{BC}\] Так как \(AC=BC\), то \(OK=BK=r\).
По теореме Пифагора \(AB=\sqrt2a\). Так как \(O\) лежит на \(AB\), то \(AO=r\), следовательно, \(OB=\sqrt2a-r\).
Тогда по теореме Пифагора из \(\triangle BOK\): \[OB^2=OK^2+BK^2 \quad\Rightarrow\quad (\sqrt2a-r)^2=r^2+r^2 \quad\Leftrightarrow\quad
r=\dfrac{\sqrt2}{\sqrt2+1}a=\sqrt2(\sqrt2-1)a.\] Так как \(a=\sqrt2+1\), то получаем \[r=\sqrt2(\sqrt2-1)(\sqrt2+1)=\sqrt2.\]
\(\sqrt2\)
Дан равнобедренный треугольник, основание которого относится к боковой стороне как \(4:3\). Найдите отношение, в котором точка касания вписанной в треугольник окружности и боковой стороны делит эту боковую сторону.
Центр вписанной в \(\triangle ABC\) окружности будет лежать на биссектрисе, проведенной к его основанию. Пусть \(AC\) – основание, \(BH\) – биссектриса, следовательно, высота и медиана. Пусть \(K\) – точка касания окружности и \(AB\). Необходимо найти, например, \(BK:KA\).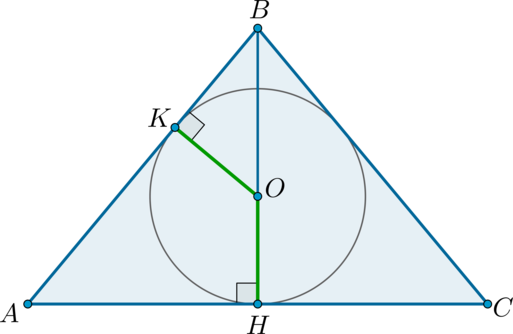
Если обозначить \(AC=4x\), \(AB=3x\), то \(AH=2x\). Заметим, что по двум углам \(\triangle BKO\sim \triangle ABH\) (\(\angle B\) – общий, а также оба прямоугольные). Следовательно, \[\dfrac{BK}{BH}=\dfrac{BO}{AB}=\dfrac{KO}{AH}\] Обозначим радиус окружности за \(r\), то есть \(KO=OH=r\). Также по теореме Пифагора \(BH=\sqrt{AB^2-AH^2}=\sqrt5x\). Следовательно, \(BO=\sqrt5x-r\). Тогда \[\dfrac{r}{2x}=\dfrac{\sqrt5x-r}{3x} \quad\Leftrightarrow\quad r=\dfrac{2\sqrt5}5x.\] Следовательно, \[BK=\dfrac{KO\cdot BH}{AH}=\dfrac{r\cdot \sqrt5x}{2x}=x \quad\Rightarrow\quad KA=3x-x=2x.\] Следовательно, \[BK:KA=1:2.\]
\(1:2\)
В треугольнике \(ABC\) на середине стороны \(AB\) отмечена точка \(M\). \(P\) – такая точка на продолжении стороны \(AC\), что \(AC=CP\). Найдите меньший из отрезков, на которые делит прямая \(MP\) сторону \(BC\), если \(BC=3\).
Пусть \(N\) – точка пересечения \(MP\) и \(BC\). Проведем \(MK\parallel BC\).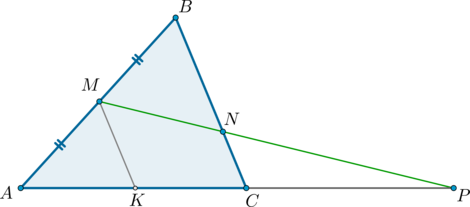
Тогда по теореме Фалеса точка \(K\) поделит \(AC\) в том же отношении, что точка \(M\) отрезок \(AB\). То есть \(AK=KC\). Следовательно, так как \(AC=CP\), то \(KC=\frac12CP\).
Заметим, что по двум углам \(\triangle NPC\sim \triangle MPK\) (\(\angle P\) – общий, \(\angle NCP=\angle MKP\) как соответственные). Следовательно, \[\dfrac{NC}{MK}=\dfrac{CP}{KP}\quad\Leftrightarrow\quad
\dfrac{NC}{MK}=\dfrac{2KC}{3KC}=\dfrac23 \quad\Leftrightarrow\quad
NC=\dfrac23MK.\] Но \(MK\) – средняя линия в \(\triangle ABC\), следовательно, \(MK=\dfrac12BC\). Откуда \(NC=\dfrac23\cdot
\dfrac12BC=\dfrac13 BC=1\). Очевидно, что \(NC<BN\), так как \(BN\) в таком случае равен \(\frac23BC=2\).
В параллелограмме \(ABCD\) точка \(M\) – середина \(BC\), а точка \(K\) – середина \(AD\). Найдите отношение длин отрезков, на которые прямые \(AM\) и \(CK\) разделили диагональ \(BD\).
Рассмотрим картинку. Пусть \(O\) – точка пересечения \(AM\) и \(BD\), а \(Q\) – точка пересечения \(CK\) и \(BD\).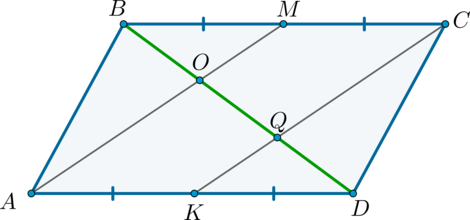
Так как у параллелограмма противоположные стороны равны, то \(AK=KD=BM=MC\).
Заметим, что \(\triangle BOM \sim \triangle AOD\) по двум углам (\(\angle AOD=\angle BOM\) как вертикальные, \(\angle OAD=\angle OMB\) как накрест лежащие). Следовательно, \[\dfrac{BO}{OD}=\dfrac{BM}{AD}=\dfrac12 \quad\Leftrightarrow\quad BO=\dfrac12OD.\] Заметим, что можно записать это так: \(BO=\dfrac13BD\).
Аналогично \(\triangle DQK\sim \triangle CQB\), следовательно, \[\dfrac{DQ}{QB}=\dfrac{KD}{BC}=\dfrac12\quad\Leftrightarrow\quad DQ=\dfrac12QB.\] Заметим, что можно записать это так: \(DQ=\dfrac13BD\).
Таким образом, \(DQ=BO=\dfrac13BD\), следовательно, \[OQ=BD-\dfrac13BD-\dfrac13BD=\dfrac13BD.\] Таким образом, \[BO:OQ:QD=1:1:1.\]
\(1:1:1\)



