Задачи на подобие треугольников и пропорциональные отрезки (страница 3)

\(\blacktriangleright\) Если на одной из сторон угла отметить равные между собой отрезки и через их концы провести параллельные прямые, то эти прямые отсекут на второй стороне также равные между собой отрезки.
\(\blacktriangleright\) Теорема Фалеса: параллельные прямые отсекают на сторонах угла пропорциональные отрезки.
Наиболее часто встречающиеся подобия треугольников:
\(\blacktriangleright\) Средняя линия треугольника отсекает от него подобный ему треугольник.
\(\blacktriangleright\) Треугольники, образованные диагоналями трапеции и основаниями, подобны.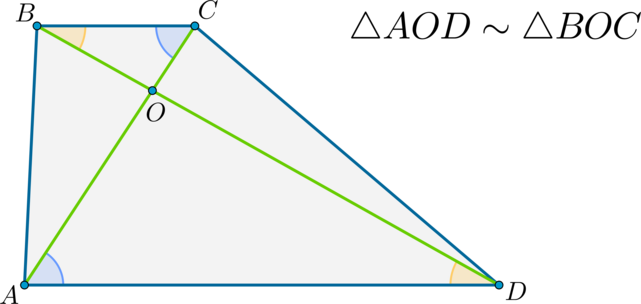
\(\blacktriangleright\) Высота прямоугольного треугольника, проведенная к гипотенузе, делит его на два подобных треугольника.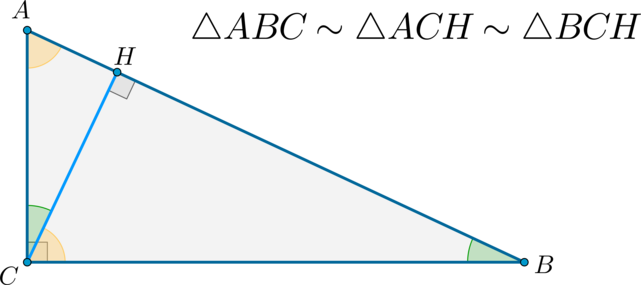
\(\blacktriangleright\) Отрезки, соединяющие основания высот треугольника, отсекают от него подобные ему треугольники.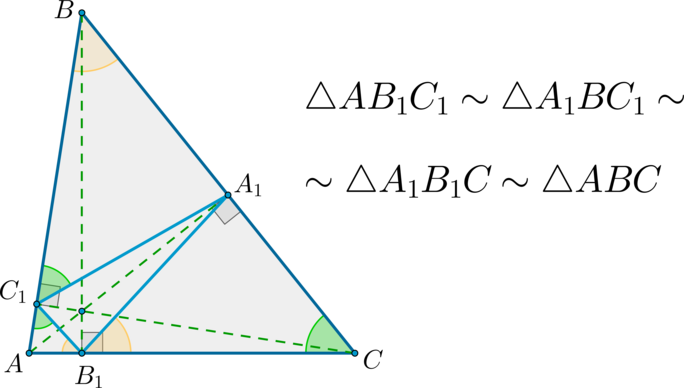
\(\blacktriangleright\) Если к окружности из одной точки вне окружности проведены две секущие, то: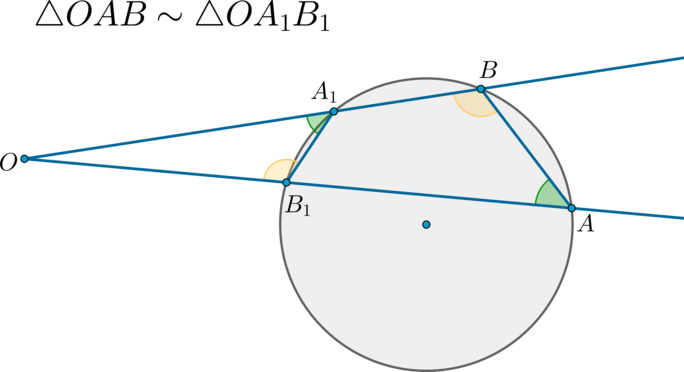
\(\blacktriangleright\) Если к окружности из одной точки проведены касательная и секущая, то: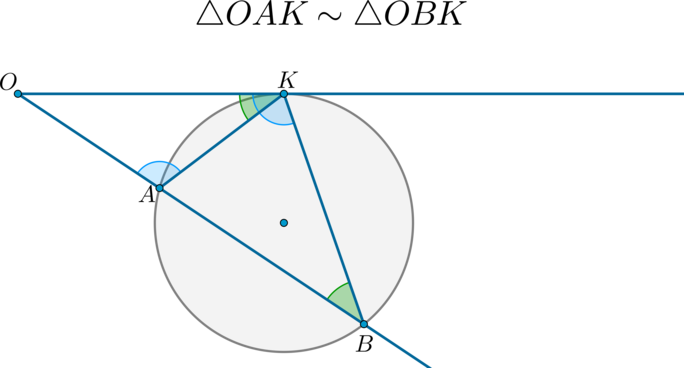
\(\blacktriangleright\) Если в окружности две хорды пересекаются, то: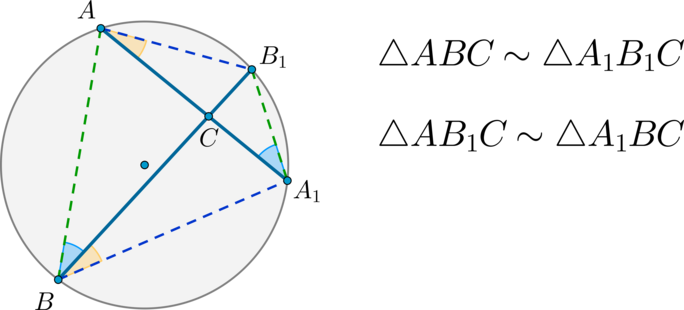
Дан параллелограмм \(ABCD\). Из вершины острого угла \(A\) проведены две прямые, делящие угол на три равные части, причем одна пересекает сторону \(BC\) в точке \(N\), а другая – сторону \(CD\) в точке \(L\), причем \(CN=CL=2\). Известно также, что \(AB=5\). Найдите \(AN+AL\).
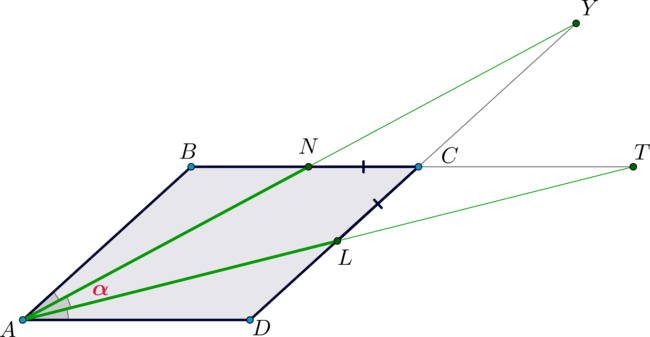
Пусть \(Y\) – точка пересечения прямых \(AN\) и \(CD\), а \(T\) – прямых \(AL\) и \(BC\). Пусть \(\frac13\angle A=\alpha\).
\(\angle CTL=\angle DAL=\alpha\) как накрест лежащие при \(AD\parallel
BC\) и секущей \(AT\). Также \(\angle CYN=\angle BAN=\alpha\) как накрест лежащие при \(AB\parallel CD\) и секущей \(AY\). Заметим, что \(\angle
NCY=\angle LCT\) как вертикальные. Следовательно, в \(\triangle NCY\) и \(\triangle LCT\) равны два угла, следовательно, равны и третьи углы. Также у них \(NC=LC\), следовательно, по признаку “сторона и два прилежащих угла” эти треугольники равны. Значит, \(CY=CT\) и \(NY=LT\).
Тогда \(\triangle ANT=\triangle ALY\), так как \(NT=LY\) и прилежащие углы равны (\(\angle NTA=\angle LYA=\alpha\) по доказанному, \(\angle ANT=\angle ALY=180^\circ-2\alpha\)). Отсюда \(AL=AN=NT=LY\).
Тогда \(\triangle ABN=\triangle ADL\) по этому же признаку (\(\angle
BAN=\angle DAL=\alpha\), \(\angle ABN=\angle ADL\) как противоположные углы параллелограмма \(\Rightarrow\) \(\angle ANB=\angle ALD\)). Значит, \(AD=AB=5\). Следовательно, \(ABCD\) – ромб. Отсюда \(BN=5-2=3\).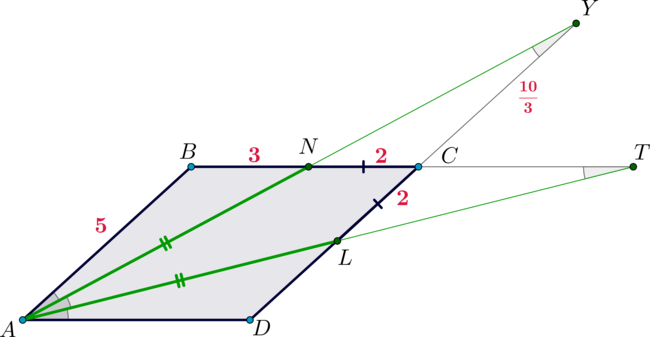
Заметим, что \(\triangle ABN\sim \triangle YCN\) по двум углам, следовательно, \[\dfrac{AB}{CY}=\dfrac{BN}{CN} \quad\Rightarrow\quad
\dfrac5{CY}=\dfrac32 \quad\Rightarrow\quad CY=\dfrac{10}3.\] Тогда по доказанному выше \(AN=AL=LY=2+\frac{10}3=\frac{16}3.\) Тогда \[AN+AL=\dfrac{32}3.\]
\(\dfrac{32}3\)
\(BB_1\) и \(CC_1\) – биссектрисы углом \(B\) и \(C\) соответственно треугольника \(ABC\). На продолжениях сторон \(AB\) и \(AC\) взяты точки \(M\) и \(L\) так, что \(BM=BC=CL\). Доказать, что \(ML\parallel B_1C_1\).
(Задача от подписчиков)
Пусть \(\angle ABC=2\alpha\), а \(\angle ACB=2\beta\). Тогда \(\angle
MBC=180^\circ-2\alpha\) и \(\angle LCB=180^\circ-2\beta\). Так как \(\triangle MBC\) равнобедренный, то в нем \(\angle M=\angle
C=\frac12\left(180^\circ-\angle MBC\right)=\alpha\). Аналогично в \(\triangle LCB\) углы \(\angle CLB=\angle CBL=\beta\).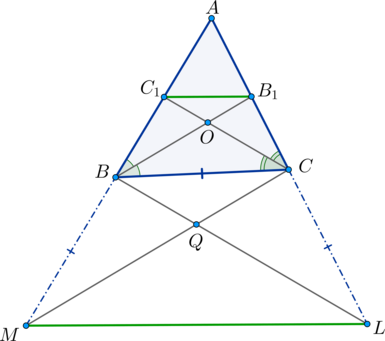
\(\angle MBQ=180^\circ-2\alpha-\beta=\angle BC_1O\). Следовательно, по двум углам \(\triangle MBQ\sim \triangle C_1BO\). Следовательно, \[\dfrac{C_1O}{BQ}=\dfrac{BO}{MQ} \qquad (1)\] Аналогично \(\triangle LCQ\sim \triangle B_1CO\), следовательно, \[\dfrac{CO}{LQ}=\dfrac{B_1O}{CQ}\qquad (2)\]
Заметим, что тогда \(\triangle BOC=\triangle BQC\) по двум углам (\(\angle OBC=\angle QCB=\alpha\), \(\angle OCB=\angle QBC=\beta\) по доказанному выше) и общей стороне. Следовательно, \(BQ=CO\), \(CQ=BO\). Значит, перемножив равенства \((1)\) и \((2)\), получим: \[\dfrac{C_1O\cdot CO}{BQ\cdot LQ}=\dfrac{B_1O\cdot BO}{MQ\cdot CQ}\quad
\Rightarrow\quad \dfrac{C_1O}{LQ}=\dfrac{B_1O}{MQ} \qquad (3)\] Заметим также, что \(\angle B_1OC_1=\angle BOC=\angle BQC=\angle
MQL \quad (*)\).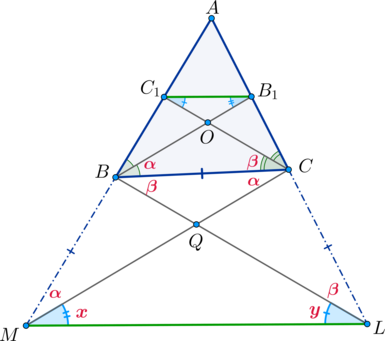
Следовательно, по двум пропорциональным сторонам (из \((3)\)) и углу между ними \(\triangle B_1OC_1\sim \triangle MQL\), откуда \[\angle OB_1C_1=\angle QML=x, \quad \angle OC_1B_1=\angle QLM=y\] Отсюда \(\angle C_1B_1C+\angle
MLC=x+(180^\circ-\alpha-2\beta)+y+\beta =
180^\circ+x+y-\alpha-\beta\).
Но из \((*)\) следует, что \(180^\circ-\alpha-\beta=\angle BOC=\angle
MQL=180^\circ-x-y\), откуда следует, что \(x+y=\alpha+\beta\). Следовательно, \[\angle C_1B_1C+\angle MLC=180^\circ\] Следовательно, это односторонние углы при прямых \(B_1C_1\) и \(ML\) и секущей \(AL\), значит, \(B_1C_1\parallel ML\).
Доказательство
Основания трапеции равны \(a\) и \(b\). Диагонали трапеции пересекаются в точке \(O\) под прямым углом. Одна из диагоналей делится точкой \(O\) на отрезки с длинами \(c_1\) и \(d_1\), а другая – на отрезки с длинами \(c_2\) и \(d_2\).
а) Докажите, что величина \[\dfrac{c_1d_1 + c_2d_2}{2}\] равна площади прямоугольного треугольника с катетами \(a\) и \(b\).
б) Найдите площадь данной трапеции, если \(ab = 100\), а \(c_2\), \(d_1\) и \(d_2\) удовлетворяют уравнению \[100\cdot\dfrac{c_2 + d_2}{d_1} - \dfrac{{c_2}^2d_2 + c_2{d_2}^2}{d_1} + d_1(c_2 + d_2) - 500 = 0.\]
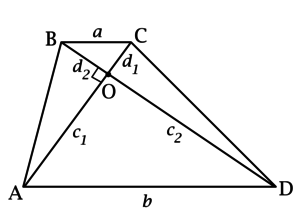
а) Пусть \(ABCD\) – данная трапеция, \(BC = a\), \(AD = b\).
Рассмотрим треугольники \(BOC\) и \(AOD\): \(\angle CBD = \angle BDA\) (как внутренние накрест лежащие при параллельных прямых \(BC\), \(AD\) и секущей \(BD\)).
Аналогично \(\angle BCA = \angle CAD\), следовательно, треугольники \(BOC\) и \(AOD\) подобны по двум углам, откуда \[\dfrac{a}{b} = \dfrac{d_2}{c_2} = \dfrac{d_1}{c_1}.\]
\(d_2 = \dfrac{a}{b}\cdot c_2\), \(d_1 = \dfrac{a}{b}\cdot c_1\), тогда \[c_1d_1 + c_2d_2 = \dfrac{a}{b}\cdot {c_1}^2 + \dfrac{a}{b}\cdot {c_2}^2 = \dfrac{a}{b}({c_1}^2 + {c_2}^2),\] но треугольник \(AOD\) – прямоугольный (\(\angle AOD = 90^\circ\)), следовательно, \(b^2 = {c_1}^2 + {c_2}^2\), откуда \[c_1d_1 + c_2d_2 = \dfrac{a}{b}({c_1}^2 + {c_2}^2) = ab\qquad\Rightarrow\qquad \dfrac{c_1d_1 + c_2d_2}{2} = \dfrac{ab}{2},\] что и требовалось доказать.
б) Площадь четырёхугольника равна полупроизведению его диагоналей на синус угла между ними, откуда \[S_{ABCD} = (c_1 + d_1)(c_2 + d_2).\]
Так как \(c_1d_1 + c_2d_2 = ab = 100\), то \(c_1 = \dfrac{100 - c_2d_2}{d_1}\), откуда \[S_{ABCD} = \left(\dfrac{100 - c_2d_2}{d_1} + d_1\right)(c_2 + d_2) = 100\cdot\dfrac{c_2 + d_2}{d_1} - \dfrac{{c_2}^2d_2 + c_2{d_2}^2}{d_1} + d_1(c_2 + d_2).\] Но по условию \[100\cdot\dfrac{c_2 + d_2}{d_1} - \dfrac{{c_2}^2d_2 + c_2{d_2}^2}{d_1} + d_1(c_2 + d_2) - 500 = 0,\] тогда \[100\cdot\dfrac{c_2 + d_2}{d_1} - \dfrac{{c_2}^2d_2 + c_2{d_2}^2}{d_1} + d_1(c_2 + d_2) = 500,\] следовательно, \(S_{ABCD} = 500\).
б) \(500\).


