Задачи на подобие треугольников и пропорциональные отрезки (страница 2)

\(\blacktriangleright\) Если на одной из сторон угла отметить равные между собой отрезки и через их концы провести параллельные прямые, то эти прямые отсекут на второй стороне также равные между собой отрезки.
\(\blacktriangleright\) Теорема Фалеса: параллельные прямые отсекают на сторонах угла пропорциональные отрезки.
Наиболее часто встречающиеся подобия треугольников:
\(\blacktriangleright\) Средняя линия треугольника отсекает от него подобный ему треугольник.
\(\blacktriangleright\) Треугольники, образованные диагоналями трапеции и основаниями, подобны.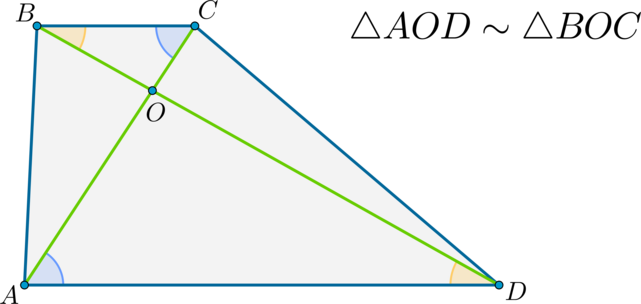
\(\blacktriangleright\) Высота прямоугольного треугольника, проведенная к гипотенузе, делит его на два подобных треугольника.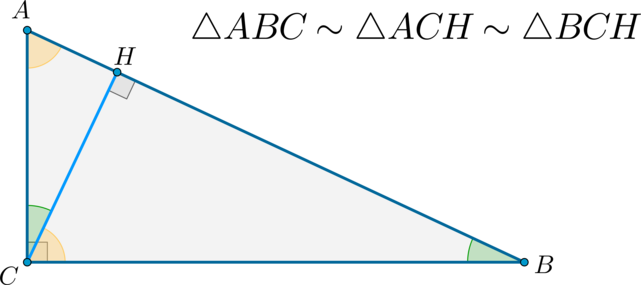
\(\blacktriangleright\) Отрезки, соединяющие основания высот треугольника, отсекают от него подобные ему треугольники.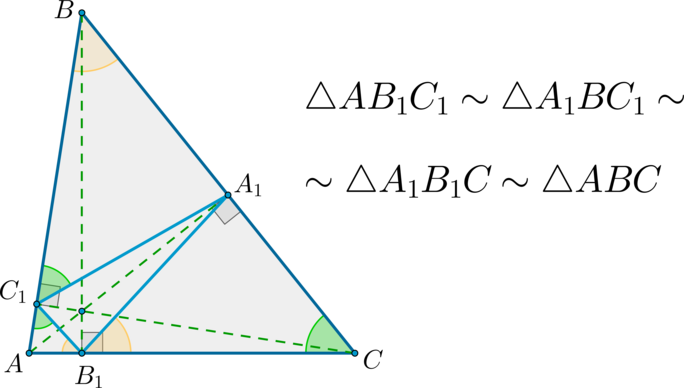
\(\blacktriangleright\) Если к окружности из одной точки вне окружности проведены две секущие, то: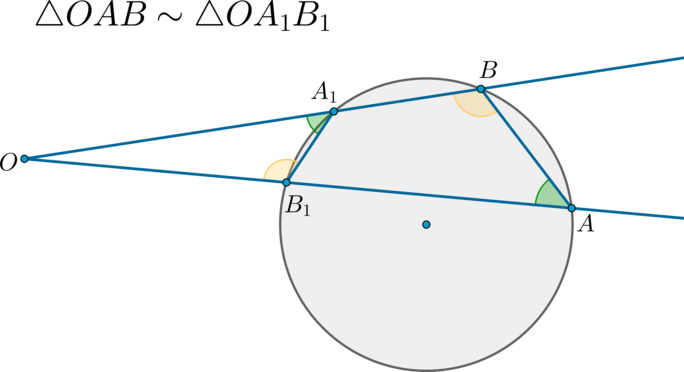
\(\blacktriangleright\) Если к окружности из одной точки проведены касательная и секущая, то: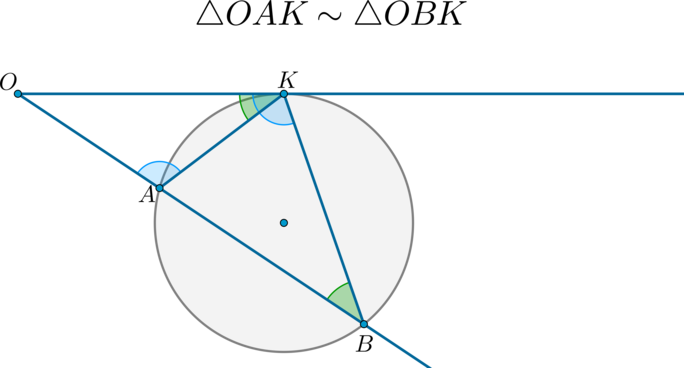
\(\blacktriangleright\) Если в окружности две хорды пересекаются, то: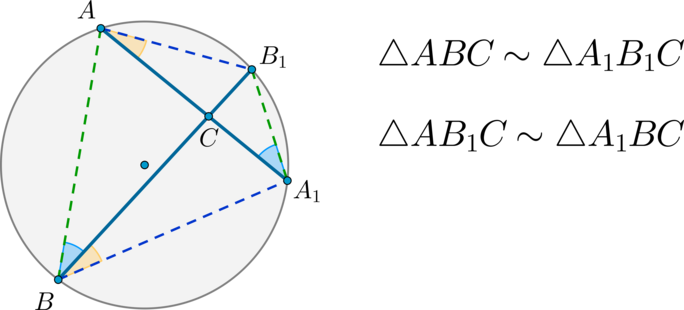
В прямоугольном треугольнике с катетами \(7\) и \(24\) проведены биссектрисы острых углов. Найдите длины этих биссектрис.

По теореме Пифагора найдем гипотенузу \(AB=25\). Так как биссектриса треугольника делит его сторону на отрезки, пропорциональные прилежащим сторонам, то \[\dfrac{CJ}{JB}=\dfrac{AC}{AB}=\dfrac{7}{25}\] Следовательно, можно принять \(CJ=7x\), \(JB=25x\), где \(x\) – некоторое число. Тогда \(7x+25x=BC=24\), откуда \(x=\frac34\). Тогда \(CJ=\frac{21}4\) и по теореме Пифагора \[AJ=\sqrt{AC^2+CJ^2}=\dfrac{35}4=8,75.\] Аналогично для биссектрисы \(BL\): \[\dfrac{AL}{LC}=\dfrac{AB}{CB}=\dfrac{25}{24}\] Следовательно, \(AL=25k\), \(LC=24k\) и \(25k+24k=AC=7\), следовательно, \(k=\frac17\). Отсюда \(CL=\frac{24}7\). Тогда по теореме Пифагора \[BL=\sqrt{CL^2+CB^2}=\dfrac{120}7\sqrt2.\]
\(8,75\) и \(\dfrac{120\sqrt2}7\)
В треугольник вписан ромб таким образом, что один угол у них общий, а противоположная вершина ромба лежит на стороне треугольника и делит ее на отрезки длинами \(14\) и \(6\). Найдите периметр треугольника, если сторона ромба равна \(7\).
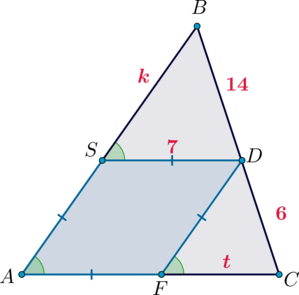
Рассмотрим рисунок. Так как по определению ромба \(SD\parallel AF\), то \(SD\parallel AC\), следовательно, \(\angle BSD=\angle BAC\). Следовательно, по двум углам (\(\angle B\) у них общий) \(\triangle BSD\sim \triangle BAC\). Обозначим \(FC=t\), \(BS=k\). Тогда имеем: \[\dfrac{SD}{AC}=\dfrac{BD}{BC} \quad\Rightarrow\quad \dfrac7{7+t}=\dfrac{14}{14+6} \quad\Rightarrow\quad t=3.\]
Аналогично \(FD\parallel AB\) и \(\triangle DFC\sim \triangle BAC\). Следовательно, \[\dfrac{DF}{BA}=\dfrac{FC}{AC} \quad\Rightarrow\quad \dfrac7{7+k}=\dfrac{t}{t+7}=\dfrac3{10}\quad\Rightarrow\quad k=\dfrac{49}3.\] Следовательно, периметр треугольника \(ABC\) равен \[7+\dfrac{49}3+14+6+3+7=53\frac13.\]
\(53\frac13\)
В треугольник со стороной \(a=10\) и высотой \(6\), проведенной к этой стороне, вписан квадрат таким образом, что две соседние вершины квадрата лежат на стороне \(a\), а две другие вершины квадрата лежат на двух других сторонах треугольника соответственно. Найдите периметр квадрата.
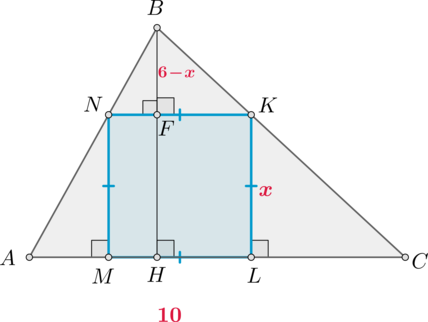
Рассмотрим рисунок.
Пусть \(AC=10\), \(BH=6\) – высота, \(MNKL\) – квадрат со стороной \(x\). Необходимо найти \(4x\).
Так как \(NK\parallel ML\), то \(NK\parallel AC\). Так как \(NM\perp AC\) и \(BH\perp AC\), то \(NM\parallel BH\). Так как отрезки параллельных прямых, заключенные между двумя параллельными прямыми, равны, то \(NM=FH=x\). Следовательно, \(BF=6-x\). Заметим, что \(\angle BKN=\angle
BCA\) как соответственные при \(NK\parallel AC\) и \(BC\) секущей. Следовательно, \(\triangle BKF\sim \triangle BCH\) по двум углам. Значит, \[\dfrac{BF}{BH}=\dfrac{BK}{BC}\qquad (1)\] Аналогично \(\triangle BKN\sim \triangle BCA\), следовательно, \[\dfrac{BK}{BC}=\dfrac{NK}{AC}\qquad (2)\] Из \((1)\) и \((2)\) можно сделать вывод, что \[\dfrac{BF}{BH}=\dfrac{NK}{AC} \quad\Rightarrow\quad
\dfrac{6-x}{6}=\dfrac{x}{10} \quad\Rightarrow\quad x=\dfrac{15}4
\quad\Rightarrow\quad 4x=15.\]
В остроугольном треугольнике \(ABC\): \(\angle B = 60^\circ\), \(AM\) и \(CN\) – высоты, а точка \(Q\) – середина \(AC\).
а) Докажите, что \(\triangle MNQ\) – равнобедренный.
б) Найдите \(\dfrac{\angle MNQ}{\angle NQM}\).
а) \(NQ\) – медиана в прямоугольном треугольнике \(ANC\), тогда \[NQ = 0,5\cdot AC,\] \(MQ\) – медиана в прямоугольном треугольнике \(AMC\), тогда \[MQ = 0,5\cdot AC = NQ.\]
б) Рассмотрим прямоугольный треугольник \(ABM\): \[\angle BAM = 90^\circ - \angle ABM = 30^\circ\qquad\Rightarrow\qquad BM = AB\cdot\sin\angle BAM = 0,5\cdot AB.\] Рассмотрим прямоугольный треугольник \(BCN\): \(\angle BCN = 90^\circ - \angle ABM = 30^\circ\), откуда \[BN = BC\cdot\sin\angle BAM = 0,5\cdot BC.\] 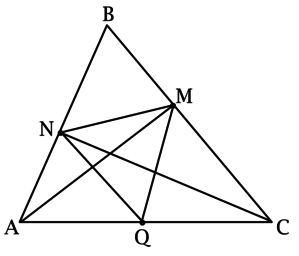
Так как \[\dfrac{1}{2} = \dfrac{BN}{BC} = \dfrac{BM}{AB},\] a \(\angle ABC\) – общий для треугольников \(BMN\) и \(ABC\), лежащий между пропорциональными сторонами, то треугольники \(BMN\) и \(ABC\) подобны, откуда \[\dfrac{MN}{AC} = \dfrac{BN}{BC} = \dfrac{1}{2},\] то есть \(MN = 0,5\cdot AC = MQ = NQ\), следовательно, \(\angle MNQ = \angle NQM\) и \[\dfrac{\angle MNQ}{\angle NQM} = 1.\]
б) \(1\).
На сторонах \(AB\) и \(BC\) треугольника \(ABC\) отмечены точки \(D\) и \(E\) соответственно, \(O\) – точка пересечения \(AE\) и \(CD\). При этом \(\angle EAC = \angle DCB\), \(\angle BAE = \angle OBC\).
а) Докажите, что \(E\) – середина \(BC\).
б) Точка \(A_1\) симметрична точке \(A\) относительно прямой \(BC\). Сколько различных окружностей можно описать около четырёхугольника \(OBA_1C\)?
а) Рассмотрим треугольники \(AEC\) и \(OEC\): \(\angle EAC = \angle DCB\), \(\angle AEC\) – общий, тогда треугольники \(AEC\) и \(OEC\) подобны (по двум углам), откуда \[\dfrac{EC}{AE} = \dfrac{OE}{EC}\qquad\Rightarrow\qquad EC^2 = OE\cdot AE.\]
Рассмотрим треугольники \(ABE\) и \(OBE\): \(\angle BAE = \angle OBC\), \(\angle AEB\) – общий, тогда треугольники \(ABE\) и \(OBE\) подобны (по двум углам), откуда \[\dfrac{BE}{AE} = \dfrac{OE}{BE}\qquad\Rightarrow\qquad BE^2 = OE\cdot AE = EC^2,\] откуда в силу того, что \(BE > 0\), \(EC > 0\), получаем: \(BE = EC\).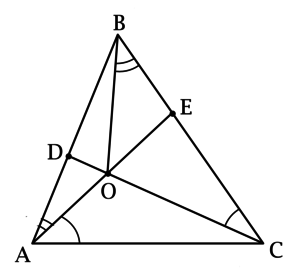
б) Пусть \(AF\) – высота в треугольнике \(ABC\). Так как точка \(A_1\) симметрична точке \(A\) относительно прямой \(BC\), то \(AF = FA_1\), тогда треугольники \(ABF\) и \(A_1BF\) равны по двум катетам (\(BF\) – общий), следовательно, \(AB = A_1B\).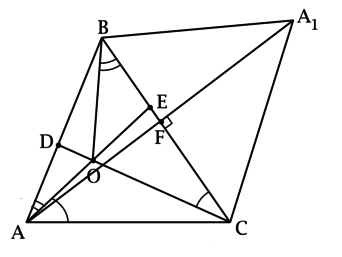
Аналогично треугольники \(AFC\) и \(A_1FC\) равны, откуда \(AC = A_1C\).
Рассмотрим треугольники \(ABC\) и \(A_1BC\): \(BC\) – общая, \(AB = A_1B\), \(AC = A_1C\), тогда треугольники \(ABC\) и \(A_1BC\) равны по трём сторонам, тогда \(\angle BAC = \angle BA_1C\). \[\angle BOC = 180^\circ - \angle OBC - \angle OCB = 180^\circ - \angle BAE - \angle EAC = 180^\circ - \angle BAC = 180^\circ - \angle BA_1C,\] тогда \(\angle BOC + \angle BA_1C = 180^\circ\). Так как \(A_1BOC\) – четырёхугольник, то сумма его углов равна \(360^\circ\), следовательно, суммы его противоположных углов равны по \(180^\circ\) и, значит, около него можно описать окружность (и притом только одну).
б) \(1\).
Вершины квадрата \(PQRS\) лежат на сторонах треугольника \(ABC\) (\(P\) лежит на \(AB\), \(Q\) и \(R\) лежат на \(BC\), \(S\) лежит на \(AC\)). \(AK\) – высота в треугольнике \(ABC\).
а) Докажите, что если \(\angle BAC = 90^\circ\), то \(BP\cdot AS = AP\cdot CS\).
б) Найдите \(\dfrac{PQ}{BC}\), если \(AK = \dfrac{1}{2}BC\).
а) Рассмотрим треугольники \(APS\) и \(PBQ\): \(\angle BQP = 90^\circ = \angle PAS\). Так как \(\angle SPQ = 90^\circ\), то \(\angle APS + \angle BPQ = 90^\circ\), откуда \(\angle APS = \angle PBQ\), следовательно, треугольники \(APS\) и \(PBQ\) подобны по двум углам.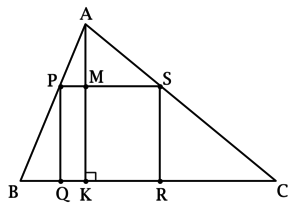
Из подобия этих треугольников получаем: \[\dfrac{PS}{BP} = \dfrac{AS}{PQ},\] но \(PS = PQ\), тогда \(PS^2 = AS\cdot BP\).
Аналогично треугольники \(APS\) и \(SCR\) подобны по двум углам, откуда \[\dfrac{PS}{SC} = \dfrac{AP}{SR},\] но \(PS = SR\), тогда \(PS^2 = AP\cdot SC\).
В итоге \[AS\cdot BP = PS^2 = AP\cdot SC,\] что и требовалось доказать.
б) Так как \(PQRS\) квадрат, то \(PS\parallel QR\), откуда следует равенство \(\angle APS = \angle ABC\) как односторонних углов при параллельных прямых и секущей, а также то, что \(AK\perp PS\). Пусть \(M\) – точка пересечения \(AK\) и \(PS\).
Рассмотрим треугольники \(APM\) и \(ABK\): \(\angle APM = \angle ABK\), \(\angle PAM\) – общий, тогда треугольники \(APM\) и \(ABK\) подобны по двум углам, откуда \[\dfrac{AM}{AK} = \dfrac{AP}{AB}.\]
Рассмотрим треугольники \(APS\) и \(ABC\): \(\angle APS = \angle ABC\), \(\angle BAC\) – общий, тогда треугольники \(APS\) и \(ABC\) подобны по двум углам, откуда \[\dfrac{PS}{BC} = \dfrac{AP}{AB}.\]
В итоге \[\dfrac{AM}{AK} = \dfrac{AP}{AB} = \dfrac{PS}{BC},\] следовательно, \[\dfrac{AK - MK}{AK} = \dfrac{PS}{BC}.\] Так как \(PQ\) и \(MK\) – отрезки параллельных прямых, заключённых между параллельными прямыми \(PS\) и \(BC\), то \(MK = PQ\).
\(PS = PQ\), \(AK = 0,5\cdot BC\), тогда \[\dfrac{0,5\cdot BC - PQ}{0,5\cdot BC} = \dfrac{PQ}{BC},\] следовательно, \(BC - 2PQ = PQ\), значит, \[BC = \dfrac{1}{3}\cdot PQ\qquad\Rightarrow\qquad \dfrac{PQ}{BC} = \dfrac{1}{3}.\]
б) \(\dfrac{1}{3}\).
В прямоугольный треугольник \(ABC\) с прямым углом \(C\) и катетами \(AC=6\) и \(BC=8\) вписана прямоугольная трапеция \(MNKB\) так, что \(MN=CK\), точки \(N\) и \(K\) лежат на катетах \(AC\) и \(BC\) соответственно, а меньшее основание параллельно гипотенузе. Найдите площадь трапеции.
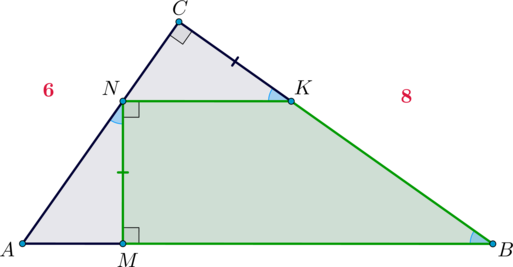
Рассмотрим рисунок. Заметим, что из условия следует, что основаниями трапеции будут \(NK\) и \(MB\). Если меньшее основание трапеции параллельно гипотенузе, то и большее ей параллельно, следовательно, и \(NK\parallel AB\), и \(MB\parallel AB\). Так как \(MB\) и \(AB\) имеют общую точку \(B\), то \(M\) лежит на \(AB\). Следовательно, отсюда однозначно определятся, как трапеция вписана в треугольник.
По теореме Пифагора гипотенуза \(AB=10\). Заметим, что \(\angle
CAB=\angle CNK\) как соответственные при \(NK\parallel AB\) и \(AC\) секущей. Значит, прямоугольные треугольники \(CNK\) и \(ANM\) равны по катету и острому углу. Следовательно, \(AN=NK\). Введем обозначения: \(AN=y\), \(CN=x\), \(CK=z\). Проведем \(KH\perp AB\).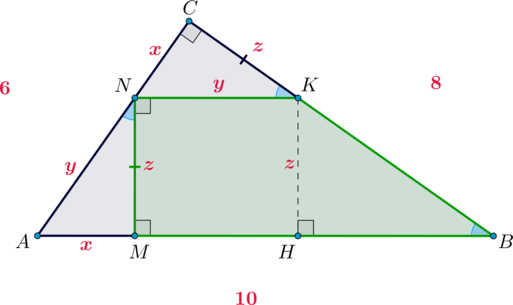
Тогда \(x+y=6\). Так как \(MH=NK=y\) (так как \(MNKH\) прямоугольник), то \(AH=x+y=6\). Следовательно, \(HB=10-6=4\). Также \(KB=CB=CK=8-z\). Следовательно, по теореме Пифагора из \(\triangle KHB\): \[(8-z)^2=z^2+4^2 \quad\Rightarrow\quad z=3.\] Заметим, что \(\angle KBH=\angle CKN\) как соответственные при \(AB\parallel NK\) и \(CB\) секущей. Следовательно, прямоугольные \(\triangle KBH\sim \triangle KCN\). Значит, \[\dfrac{KB}{NK}=\dfrac{KH}{CN}=\dfrac{HB}{CK} \quad\Rightarrow\quad \dfrac5y=\dfrac3x=\dfrac43 \quad\Rightarrow\quad x=\dfrac94 \quad {\small{\text{и}}} \quad y=\dfrac{15}4.\] Тогда площадь трапеции равна \[S=\dfrac{NK+MB}2\cdot NM=\dfrac{69}4.\]



