Логарифмические неравенства с числовым основанием —Каталог задач по ЕГЭ - Математика

Ошибка.
Попробуйте повторить позже

Задача 1#492

Решите неравенство

2 log2x ≥ 1.

Показать ответ и решение

Найдем ОДЗ:

2 x > 0 ⇔ x ⁄= 0

При $x⁄= 0$ исходное неравенство равносильно неравенству

2 log2x ≥log22 x2 ≥2

Отсюда получаем

( √-] [√ - ) x ∈ −∞;− 2 ∪ 2;+ ∞

Сюда не вошёл $x= 0,$ следовательно, это и есть ответ.

Ответ:

$(− ∞;− √2]∪ [√2;+∞ )$

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	2

Обоснованно получен ответ, отличающийся от верного исключением/включением граничных точек,	1
ИЛИ
получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	2

При этом в первом случае выставления 1 балла допускаются только ошибки в строгости неравенства: « $<$ » вместо « $≤$ » или наоборот. Если в ответ включено значение переменной, при котором одна из частей неравенства не имеет смысла, то выставляется оценка «0 баллов».

Ошибка.
Попробуйте повторить позже

Задача 2#493

Решите неравенство

2 log2 x ≥ 1+ log2x.

Показать ответ и решение

Найдем ОДЗ:

{ x2 > 0 ⇔ x >0 x> 0

При $x> 0$ исходное неравенство равносильно неравенствам

log2x2 ≥ log22+ log2x ⇔ log2x2 ≥ log22x 2 x ≥ 2x ⇔ x(x− 2)≥ 0

По методу интервалов имеем:

$PIC$

То есть получаем

x ∈(− ∞;0]∪[2;+∞ )

С учетом $x> 0$ получаем решение исходного неравенства

x ∈[2;+∞ )

Ответ:

$[2;+ ∞ )$

Ошибка.
Попробуйте повторить позже

Задача 3#2353

Решите неравенство

log35x+ log5x ≥ 0.

Показать ответ и решение

Найдем ОДЗ: $x> 0.$

Сделаем замену $t =log5x.$ Тогда имеем:

3 2 t + t≥ 0 ⇔ t(t + 1)≥ 0

Так как $t2 ≥ 0,$ то $t2+ 1≥ 1> 0,$ следовательно, последнее неравенство равносильно неравенству

t≥ 0

Отсюда получаем

log5x≥ 0 ⇔ log5x ≥ log51 ⇔ x ≥1

С учётом ОДЗ получаем окончательно

x ∈[1;+∞ )

Ответ:

$[1;+ ∞ )$

Ошибка.
Попробуйте повторить позже

Задача 4#2669

Решите неравенство

2 log2x+ 3log2x+ 3≤ 1

Показать ответ и решение

Найдем ОДЗ: $x> 0.$

Исходное неравенство равносильно неравенству

2 log2x+ 3log2x+ 2≤ 0

Сделаем замену $t =log x: 2$

t2+ 3t+ 2≤ 0 ⇔ (t+ 1)(t+ 2) ≤0

По методу интервалов имеем:

$PIC$

Отсюда $t∈ [−2;−1].$

Тогда $− 2 ≤ log2x≤ − 1,$ что равносильно

1 1 1 1 log24 ≤log2x≤ log2 2 ⇔ 4 ≤ x≤ 2

С учётом ОДЗ получим

x∈ [0,25;0,5]

Ответ:

$[0,25;0,5]$

Ошибка.
Попробуйте повторить позже

Задача 5#494

Решите неравенство

log (x + 11)2 ≥ 2 log √-√x--+ log (x + 11)8 5 5 625

Показать ответ и решение

ОДЗ:

( |{ (x + 11)2 > 0 √ -- ⇔ x > 0. |( x > 0 (x + 11)8 > 0

При $x > 0$ :
исходное неравенство равносильно неравенству

2 0,5 8 log5(x + 11) ≥ 2 log50,5 x + log54(x + 11 ) ⇔ ⇔ log5 (x + 11)2 ≥ 2log5x + log5(x + 11)2 ⇔ ⇔ 0 ≥ 2 log5 x ⇔ 0 ≥ log5 x ⇔ log5 1 ≥ log5x ⇔ 1 ≥ x.

Таким образом, с учётом ОДЗ ответ:

x ∈ (0;1].

Ответ:

$(0;1]$

Ошибка.
Попробуйте повторить позже

Задача 6#495

Решите неравенство

log (x − 2)2016 ≥ log √x--+ log (x − 2)−4032 4 2 0,0625

Показать ответ и решение

ОДЗ:

( |{ (x − 2)2016 > 0 √ -- ⇔ x ∈ (0;2) ∪ (2;+ ∞ ). |( x > 0 (x − 2)−4032 > 0

На ОДЗ:
исходное неравенство равносильно неравенству

2016 0,5 − 4032 log4(x − 2) ≥ log40,5 x + log4−2(x − 2) ⇔ ⇔ log4(x − 2 )2016 ≥ log4 x + log4(x − 2)2016 ⇔ ⇔ 0 ≥ log4 x ⇔ log4 1 ≥ log4x ⇔ 1 ≥ x.

Таким образом, с учётом ОДЗ ответ:

x ∈ (0;1].

Ответ:

$(0;1]$

Ошибка.
Попробуйте повторить позже

Задача 7#496

Решите неравенство

log3(x2 + x + 0,5) + 3log (x2 + x + 0,5)π + 4e > 0 4 4

Показать ответ и решение

ОДЗ:

x2 + x + 0,5 > 0

На ОДЗ:

3 log4(x2 + x + 0,5)π = 3π ⋅ log4 (x2 + x + 0, 5)

Сделаем замену $log4(x2 + x + 0,5) = t$ :

3 t + 3πt + 4e > 0

Рассмотрим, какие значения может принимать $t$

t = log (x2 + x + 0,5) = log ((x + 0,5)2 + 0,25) ≥ log 0,25 = − 1 4 4 4

Покажем, что при всех $t ≥ − 1$ неравенство

3 t + 3πt + 4e > 0

выполнено.
Обозначим $f (t) = t3 + 3πt + 4e$ , тогда

f′(t) = 3t2 + 3π > 0,

следовательно, $f (t)$ – всюду возрастает, тогда при $t ≥ − 1$ выполнено

f (t) ≥ f (− 1 ) = − 1 − 3π + 4e > − 1 − 3 ⋅ 3,15 + 4 ⋅ 2,7 = 0,35 > 0

Таким образом, исходное неравенство выполнено при

x ∈ (− ∞; + ∞ ).

Ответ:

$(− ∞; + ∞ )$

Ошибка.
Попробуйте повторить позже

Задача 8#497

Решите неравенство

log2(x2 + 2x) − 10 log (4x2 + 8x ) > − 26 4 4

Показать ответ и решение

ОДЗ:

{ x2 + 2x > 0 2 4x + 8x > 0

На ОДЗ:

log (4x2 + 8x) = log (4 ⋅ (x2 + 2x )) = 1 + log (x2 + 2x) 4 4 4

Сделаем замену $log (x2 + 2x) = t 4$ :

2 2 t − 10t − 10 > − 26 ⇔ t − 10t + 16 > 0 ⇔ (t − 2)(t − 8) > 0

По методу интервалов:

$PIC$

откуда $t ∈ (− ∞; 2) ∪ (8;+ ∞ )$ , тогда
$log4(x2 + 2x ) ∈ (− ∞; 2) ∪ (8;+∞ )$ , следовательно, с учётом ОДЗ

[ 0 < x2 + 2x < 16 8 2 4 < x + 2x

Аналогично по методу интервалов находим, что
решение неравенства $x2 + 2x > 0$ (совпадающего с ОДЗ) имеет вид: $x ∈ (− ∞; − 2) ∪ (0;+ ∞ )$
решение неравенства $x2 + 2x < 16$ имеет вид: $x ∈ (− 1 − √17; − 1 + √17-)$
их пересечение:

√ --- √ --- x ∈ (− 1 − 17;− 2) ∪ (0;− 1 + 17)

решение неравенства $2 8 x + 2x > 4$ имеет вид:

√ -----8 √ -----8 x ∈ (− ∞; − 1 − 1 + 4 ) ∪ (− 1 + 1 + 4 ;+∞ )

решение полученной совокупности неравенств с учётом ОДЗ:

√ ------ √ --- √--- √ ------ x ∈ (− ∞; − 1 − 1 + 48 ) ∪ (− 1 − 17; − 2 ) ∪ (0;− 1 + 17 ) ∪ (− 1 + 1 + 48;+ ∞ ).

Ответ:

$√ ------ √ --- √ --- √ ------ (− ∞; − 1 − 1 + 48) ∪ (− 1 − 17;− 2) ∪ (0;− 1 + 17) ∪ (− 1 + 1 + 48;+∞ )$

Ошибка.
Попробуйте повторить позже

Задача 9#498

Решите неравенство

log (xeπ) + 2016 > log (xπe ) + 2016 2 2

Показать ответ и решение

ОДЗ:

{ xeπ > 0 e ⇔ x > 0. xπ > 0

При $x > 0$ :
исходное неравенство равносильно неравенству

π e xe > xπ ,

что при $x > 0$ равносильно неравенству

eπ > πe.

Так как $eπ > 0$ и $πe > 0$ , то последнее неравенство равносильно неравенству

ln e ln π ln(eπ) > ln (πe ) ⇔ π ln e > eln π ⇔ ----> ---, e π

то есть осталось сравнить значение функции $lnx f (x) = ---- x$ в точках $e$ и $π$ .

1 f ′(x) = x ⋅-x −-1 ⋅ ln-x-= 1-−-ln-x. x2 x2

При $x > e$ : $′ f (x ) < 0$ , следовательно, на $(e;+ ∞ )$ функция $f (x)$ убывает (при этом $x = e$ – точка локального максимума функции $f$ ), следовательно,

ln-e- ln-π π e f (e) > f (π) ⇒ e > π ⇒ e > π ,

то есть исходное неравенство (с учётом ОДЗ) выполнено при

x > 0.

Ответ:

$(0;+ ∞ )$

Ошибка.
Попробуйте повторить позже

Задача 10#845

Решите неравенство

√ -- log √1-(x2 + 3x − 2x ) > − 2 418

Показать ответ и решение

ОДЗ:

√ -- √ -- √ -- x2 + 3x − 2x > 0 ⇔ x(x + 3 − 2) > 0 ⇔ x ∈ (− ∞; 2 − 3) ∪ (0;+ ∞ ).

Решим данное неравенство на ОДЗ. Оно равносильно неравенству

√ -- ( 1 ) −2 √ -- √ -- log-4√1-(x2 + 3x − 2x) > log-14√-- 4√---- ⇔ log√14--(x2 + 3x − 2x) > log 4√1- 3 2 18 18 18 18 18

Т.к. основание логарифмов меньше единицы ( $1 -4√18 < 1$ ), то неравенство равносильно

2 √ -- √ -- 2 √-- √ -- √ -- √ -- x +3x − 2x < 3 2 ⇔ x +(3 − 2 )x − 3 2 < 0 ⇔ (x − 2 )(x+3 ) < 0 ⇔ x ∈ (− 3; 2).

Пересечем решение с ОДЗ. Учитывая, что $√2--− 3 > − 3$ , $0 < √2--$ , получаем окончательный ответ: $√ -- √ -- x ∈ (− 3; 2 − 3) ∪ (0; 2)$ .

Ответ:

$√ -- √ -- (− 3; 2 − 3) ∪ (0; 2)$

Ошибка.
Попробуйте повторить позже

Задача 11#846

Решите неравенство

logx2 25 + logx −2(x − 2)2 ≥ logx(3x2)

Показать ответ и решение

ОДЗ:

( || x2 > 0 ||| 2 ( |||| x ⁄= 1 |||| x ⁄= 0 ||| x − 2 > 0 ||| x ⁄= ±1 |{ x − 2 ⁄= 1 |{ x > 2 ⇔ ⇔ x ∈ (2;3) ∪ (3;+∞ ). ||| (x − 2)2 > 0 ||| x ⁄= 3 ||| 3x2 > 0 ||| x ⁄= 2 |||| ||( ||| x > 0 x > 0 ( x ⁄= 1

Решим неравенство на ОДЗ. Т.к. из ОДЗ следует, что $x > 2$ , то

1) log 25 = log 5 = log 5 x2 |x| x 2) logx− 2(x − 2)2 = 2 3) log (3x2) = log 3 + log x2 = log 3 + 2 x x x x

Следовательно, неравенство на ОДЗ равносильно

5 logx 5 + 2 ≥ 2 + logx 3 ⇔ logx 5 ≥ logx 3 ⇔ logx --≥ 0 3

Т.к. $1 loga b = log-a- b$ , то полученное неравенство равносильно

--1--- ≥ 0 ⇔ log5 x > 0 ⇔ x > 1. log53 x 3

Пересекая ответ с ОДЗ, получим $x ∈ (2;3) ∪ (3;+ ∞ )$ .

Заметим, что на ОДЗ логарифм может быть равен нулю тогда и только тогда, когда его аргумент равен 1, и больше нуля, когда основание и аргумент лежат по одну сторону от 1. Следовательно, $5 logx -- 3$ не может быть равен 0, а больше нуля он тогда и только тогда, когда основание $x$ больше 1. То есть неравенство $5 logx --≥ 0 3$ равносильно $x > 1$ .

Ответ:

$(2;3) ∪ (3;+ ∞ )$

Ошибка.
Попробуйте повторить позже

Задача 12#847

Решите неравенство

( ) log2 2log4x4 > log−8 1log4log22562

Показать ответ и решение

ОДЗ:

{ { x4 > 0 x ⁄= 0 2 4 ⇔ 4 ⇔ (x + 1)(x − 1)(x + 1) > 0 ⇔ x ∈ (− ∞; − 1) ∪ (1;+ ∞ ). 2 log4 x > 0 x > 1

Решим неравенство на ОДЗ. Преобразуем правую часть:

( )−1 ( 1) −1 log−8 1log4 log22562 = log8 log4 log2 216 = (log8log416 )− 1 = (log8 2)−1 = -- = 3. 3

Таким образом, неравенство равносильно

( 4) ( 4) log2 2log4 x > 3 ⇔ log2 2 log4 x > log28

Т.к. основание логарифма больше единицы ( $2 > 1$ ), то неравенство на ОДЗ равносильно

2log4 x4 > 8 ⇔ log4x4 > 4 ⇔ log4 x4 > log4 44

Т.к. основание логарифма больше единицы ( $4 > 1$ ), то неравенство на ОДЗ равносильно

4 4 2 2 x > 4 ⇔ (x + 4 )(x − 4)(x + 4 ) > 0 ⇔ x ∈ (− ∞; − 4) ∪ (4;+ ∞ ).

Пересекая ответ с ОДЗ, получаем $x ∈ (− ∞; − 4) ∪ (4;+ ∞ )$ .

Ответ:

$(− ∞; − 4) ∪ (4;+ ∞ )$

Ошибка.
Попробуйте повторить позже

Задача 13#1187

Решите неравенство

( ) log6√4- log1(x + 3) ≥ 3 5

(Задача от подписчиков)

Показать ответ и решение

Обозначим $log 15(x + 3) = t$ . Тогда неравенство примет вид ( $6√ -- 1 4 = 46$ ):

log 6√-t ≥ 3 ⇔ 6 log t ≥ 3 ⇔ log t ≥ 1- 4 4 4 2

Так как основание логарифма $4 > 1$ , то данное неравенство равносильно:

{ t > 0 1 ⇔ t ≥ 2 t ≥ 42

Таким образом, получаем

log 1(x + 3 ) ≥ 2 5

Так как основание логарифма $1< 1 5$ , то неравенство равносильно:

( { x + 3 > 0 ( ) ⇔ − 3 < x ≤ − 74- ( x + 3 ≤ 1 2 25 5

Ответ:

$( ] − 3; − 7425$

Ошибка.
Попробуйте повторить позже

Задача 14#1235

Решите неравенство

( ) log64x4 ⋅ log0,58x 2 ≤ 3

Показать ответ и решение

ОДЗ неравенства: $64x > 0,64x ⁄= 1,8x > 0$ , то есть $( ) ( ) x ∈ 0; 164- ∪ 614;+ ∞$ .

Решим неравенство на ОДЗ.
Первый логарифм преобразуется в

1 1 1 log64x 4 = log-64x- = -1-----------------= ----1------ 4 2 (log264 + log2x ) 3 + 2 log2 x

Второй логарифм преобразуется:

log0,58x = − (log2 8 + log2 x) = − 3 − log2 x

Сделаем замену: $log2 x = t$ . Тогда неравенство примет вид:

2 ---1-- ⋅ (− 3 − t)2 ≤ 3 ⇔ 2(t +-3)-−-3(t +-6)≤ 0 ⇔ t(2t +-9)≤ 0 3 + 12t t + 6 t + 6

Решая данное неравенство методом интервалов, получаем:

[ 9 ] t ∈ (− ∞; − 6 ) ∪ −--;0 2

Сделаем обратную замену:

⌊ ⌊ ⌊ −6 x < 1-- log2x < − 6 x < 2 || 64 ⌈ 9 ⇔ ⌈ 9 ⇔ | − --≤ log2x ≤ 0 2−2 ≤ x ≤ 20 ⌈ --1√---≤ x ≤ 1 2 16 2

Пересекая полученный ответ с ОДЗ, получаем:

( ) [ ] 1 1 x ∈ 0; 64- ∪ --√--;1 16 2

Ответ:

$( ) [ ] x ∈ 0; 164 ∪ 161√2;1$

Ошибка.
Попробуйте повторить позже

Задача 15#1799

Решите неравенство

2 log x ⋅ (log x − 2) ≥ − 1,5 4 4

Показать ответ и решение

ОДЗ:

x > 0

Сделаем замену $log2x = t$ с учётом того, что на ОДЗ $log4 x = 0,5 log2 x$ :

t(0,5t − 2) ≥ − 1,5 ⇔ t2 − 4t + 3 ≥ 0

По методу интервалов:

$PIC$

откуда $t ∈ (− ∞; 1] ∪ [3; +∞ )$ , тогда
$log2 x ∈ (− ∞; 1] ∪ [3;+ ∞ )$ , следовательно, с учётом ОДЗ

x ∈ (0;2] ∪ [8;+ ∞ ).

Ответ:

$(0;2] ∪ [8;+ ∞ )$

Ошибка.
Попробуйте повторить позже

Задача 16#1800

Решите неравенство

7- -1 2 2 lnt2 + ln t < − 10

Показать ответ и решение

ОДЗ:

t > 0

Сделаем замену $lnt = y$ с учётом того, что на ОДЗ $1- ln t2 = − 2lnt$ :

y2 − 7y + 10 < 0 ⇔ (y − 2)(y − 5) < 0

По методу интервалов:

$PIC$

откуда $y ∈ (2;5)$ , тогда
$ln t ∈ (2;5 )$ , следовательно, с учётом ОДЗ

2 5 t ∈ (e ;e ).

Ответ:

$(e2;e5)$

Ошибка.
Попробуйте повторить позже

Задача 17#1801

Решите неравенство

2 log3(x +1) ≤log3x+ log9(x+ 2)

Показать ответ и решение

Найдем ОДЗ:

( |{ x+ 1> 0 | x> 0 ⇔ x > 0 ( (x + 2)2 > 0

При $x> 0$ исходное неравенство равносильно неравенствам

log3(x+ 1)≤ log3x + log32(x+ 2)2 log3(x+ 1)≤ log3x +log3|x +2| (x+ 1) log3x-⋅(x+-2) ≤0 (x +1) x-⋅(x-+-2) ≤ 1 (x-+1)−-x-⋅(x-+2)-≤0 x ⋅2(x + 2) −x-−-x+-1-≤0 x ⋅(x + 2) x2+-x-− 1 ≥ 0 x ⋅(x + 2)

По методу интервалов на ОДЗ имеем:

$PIC$

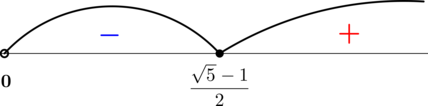
Таким образом, получаем $[√- ) x ∈ -5-− 1;+ ∞ . 2$

Ответ:

$[0,5(√5− 1);+∞ )$

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	2

Обоснованно получен ответ, отличающийся от верного исключением/включением граничных точек,	1
ИЛИ
получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	2

При этом в первом случае выставления 1 балла допускаются только ошибки в строгости неравенства: « $<$ » вместо « $≤$ » или наоборот. Если в ответ включено значение переменной, при котором одна из частей неравенства не имеет смысла, то выставляется оценка «0 баллов».

Ошибка.
Попробуйте повторить позже

Задача 18#1802

Решите неравенство

2( 2 ) ( 2 )3 log2 x − 2x + 5 − log2 x − 2x + 5 + 2 ≤0

Показать ответ и решение

Найдем ОДЗ:

2 x − 2x+ 5> 0

На ОДЗ имеем:

( 2 )3 ( 2 ) log2 x − 2x+ 5 = 3log2 x − 2x+ 5

Сделаем замену $log (x2− 2x+ 5)= t: 2$

2 t − 3t+2 ≤ 0 (t− 1)(t− 2)≤ 0

По методу интервалов имеем:

$PIC$

Отсюда получаем $t∈ [1;2],$ тогда

( 2 ) log2 x − 2x +5 ∈ [1;2]

Заметим, что

2 2 x − 2x+ 5= (x− 1) + 4≥ 4

Следовательно,

( 2 ) log2 x − 2x+ 5 ≥ log2 4= 2

Таким образом, подходят только те $x,$ при которых

( 2 ) log2 x − 2x+ 5 = log24

Отсюда получаем окончательно $x = 1.$

Ответ: 1

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	2

Обоснованно получен ответ, отличающийся от верного исключением/включением граничных точек,	1
ИЛИ
получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	2

При этом в первом случае выставления 1 балла допускаются только ошибки в строгости неравенства: « $<$ » вместо « $≤$ » или наоборот. Если в ответ включено значение переменной, при котором одна из частей неравенства не имеет смысла, то выставляется оценка «0 баллов».

Ошибка.
Попробуйте повторить позже

Задача 19#1803

Может ли множество решений неравенства вида

log f (x ) ≤ log g(x) 2 2

совпадать с

(0;1) ∪ (2;3) ∪ (4;5) ∪ ...

при некоторых функциях $f(x)$ и $g (x )$ , таких что у них совпадает область определения и на области определения всюду $f(x) > 0$ , $g(x) > 0$ ?

Показать ответ и решение

ОДЗ:

{ f (x) > 0 g (x ) > 0

На ОДЗ:
исходное неравенство равносильно неравенству

f(x) ≤ g(x ).

Таким образом, достаточно положить $g(x) = f(x) + 1$ , а $f(x)$ выбрать так, чтобы $f (x) > 0$ выполнялось на $(0;1) ∪ (2;3) ∪ (4;5 ) ∪ ...$ .

Например, определим $f (x)$ как функцию, область определения которой $(0;1) ∪ (2;3) ∪ (4;5) ∪ ...$ и на области определения