1.17 Окружность: описанная около многоугольника
Ошибка.
Попробуйте повторить позже
Четырехугольник вписан в окружность. Угол
равен
угол
равен
Найдите угол
Ответ
дайте в градусах.

Вписанные углы, опирающиеся на равные дуги, равны. Следовательно,
Тогда имеем:
Ошибка.
Попробуйте повторить позже
Два угла вписанного в окружность четырехугольника равны и
Найдите больший из оставшихся углов. Ответ дайте в
градусах.
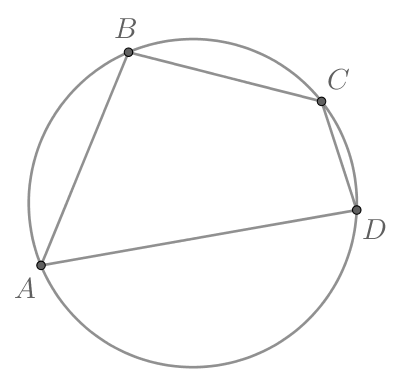
Так как четырехугольник вписан в окружность, то сумма его противоположных углов равна Так как
то
нам даны градусные меры не противоположных углов. Следовательно, нам даны градусные меры односторонних углов. Допустим
Тогда наибольшим из оставшихся углов будет
Ошибка.
Попробуйте повторить позже
Четырехугольник вписан в окружность. Угол
равен
угол
равен
Найдите угол
Ответ
дайте в градусах.
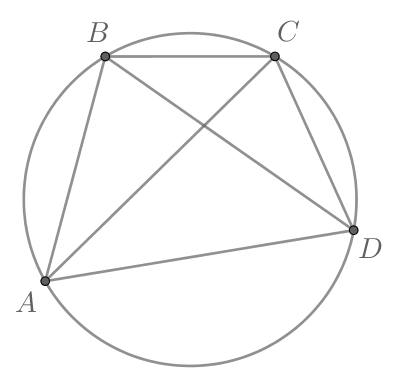
Так как вписанный угол равен половине дуги, на которую он опирается, то
Аналогично меньшая дуга (см.рис.). Следовательно, меньшая дуга
(см.рис.).
Значит как вписанный и опирающийся на дугу, равную
сам равен
Ошибка.
Попробуйте повторить позже
Угол четырехугольника
вписанного в окружность, равен
Найдите угол
этого четырехугольника. Ответ дайте
в градусах.
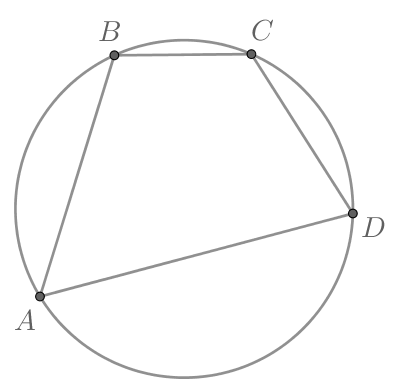
Так как четырехугольник вписан в окружность, то сумма его противоположных углов равна Следовательно,
Отсюда получаем
Ошибка.
Попробуйте повторить позже
Четырёхугольник вписан в окружность. Угол
равен
угол
равен
Найдите угол
Ответ
дайте в градусах.

Так как вписанные углы, опирающиеся на одну дугу, равны, то поскольку эти углы опираются на дугу
Тогда искомый угол равен
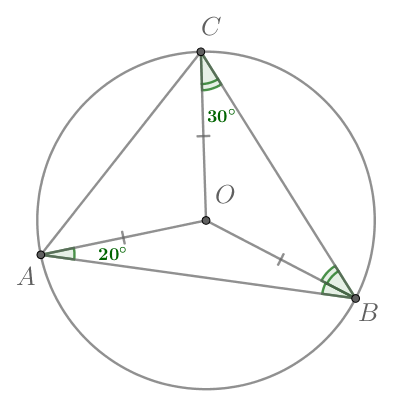
Ошибка.
Попробуйте повторить позже
Около треугольника описана окружность с центром в точке
Найдите
Ответ дайте
в градусах.
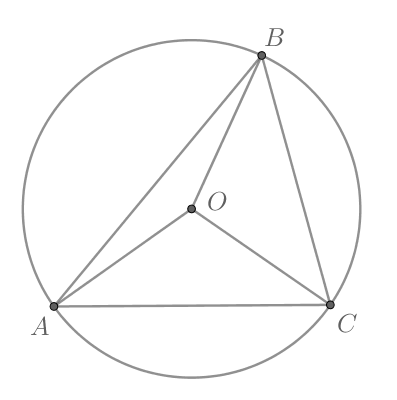
Рассмотрим картинку:
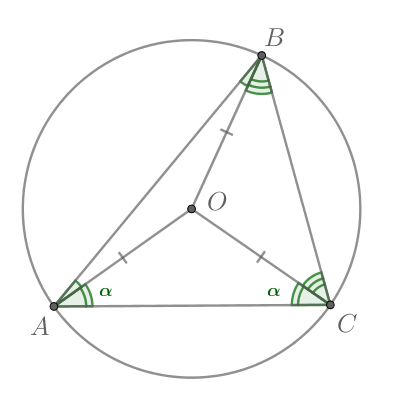
Т.к. треугольники
— равнобедренные, то
Т.к. сумма углов треугольника равна
то
Ошибка.
Попробуйте повторить позже
Около треугольника описана окружность с центром в точке
Найдите
Ответ дайте
в градусах.
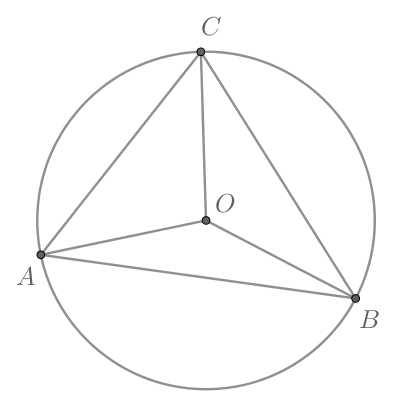
Рассмотрим картинку:
Т.к. треугольники
— равнобедренные, то
Следовательно,
Т.к. — центральный угол, опирающийся на ту же дугу
что и вписанный
то
Ошибка.
Попробуйте повторить позже
Во вписанном четырехугольнике противоположные стороны попарно равны
и
Найдите радиус описанной около
этого четырехугольника окружности.
Рассмотрим картинку:
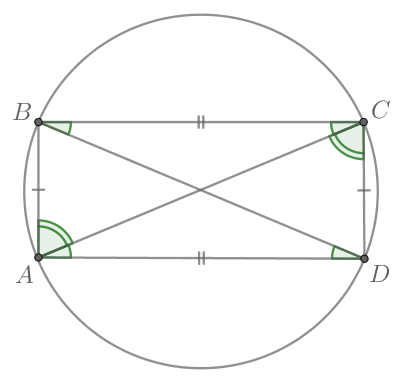
Т.к. хорды и
равны, то равны дуги
и
Следовательно, вписанные углы, опирающиеся на эти дуги, будут
тоже равны:
Таким образом, — накрест лежащие при прямых
и
и секущей
следовательно,
Аналогичным образом доказывается, что
Таким образом, — параллелограмм. Т.к. он вписанный, то это — прямоугольник.
В прямоугольнике центр описанной окружности лежит на пересечении диагоналей. Следовательно, по теореме Пифагора
Замечание.
Можно было доказать, что — прямоугольник, другим способом:
по трем сторонам. Следовательно,
Но т.к. четырехугольник вписанный, то сумма
противоположных углов равна
следовательно,
Отсюда следует, что
Аналогично
По признаку четырехугольник, у которого все углы прямые, является прямоугольником.
Ошибка.
Попробуйте повторить позже
Радиус описанной около четырехугольника окружности равен
Найдите площадь этого четырехугольника, если известно,
что все его стороны равны.
Рассмотрим картинку:
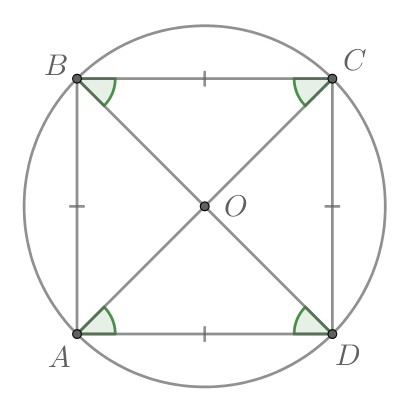
Докажем, что данный четырехугольник является квадратом.
Т.к. хорды и
равны, то равны дуги
и
Следовательно, вписанные углы, опирающиеся на эти дуги, будут
тоже равны:
Таким образом, — накрест лежащие при прямых
и
и секущей
, следовательно,
Аналогичным образом доказывается, что
Таким образом, — параллелограмм. Т.к. он вписанный, то это — прямоугольник. Т.к. все его стороны равны, то это
квадрат.
В квадрате центр описанной окружности лежит на пересечении диагоналей, следовательно, По свойству квадрата
Следовательно, площадь
Замечание.
Можно было доказать, что — квадрат, другим способом:
по трем сторонам. Следовательно,
Но т.к. четырехугольник вписанный, то сумма
противоположных углов равна
следовательно,
Отсюда следует, что
Аналогично
По признаку четырехугольник, у которого все углы прямые, является прямоугольником. Но т.к. у него еще и все
стороны равны, то это квадрат.
Ошибка.
Попробуйте повторить позже
В окружность вписан пятиугольник причем
Найдите
Ответ дайте в
градусах.

Рассмотрим картинку:

Т.к. равные хорды стягивают равные дуги, то меньшие полуокружности дуги
равны:
Пусть
Следовательно, вписанный угол
Т.к. градусная мера всей окружности равна то
Решая систему из уравнений и
получаем, что
Следовательно,
Ошибка.
Попробуйте повторить позже
Около пятиугольника описана окружность, причем
— точка пересечения отрезков
и
Найдите
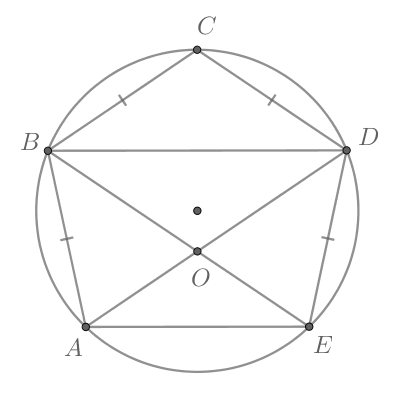
Рассмотрим картинку:
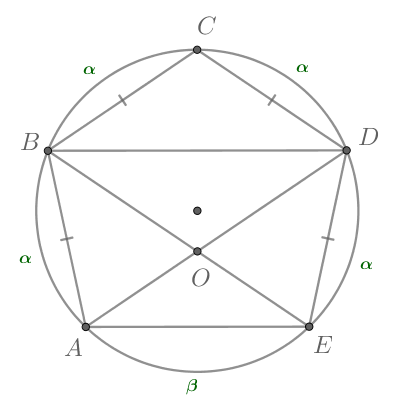
1) Т.к. равные хорды стягивают равные дуги, то меньшие полуокружности дуги
равны:
Пусть также
2)
Заметим, что вся окружность равна следовательно,
откуда
Таким образом,
и
=– односторонние углы при прямых
и
и секущей
Следовательно,
Аналогично доказывается, что
3) Значит, — параллелограмм (
). А в параллелограмме противоположные стороны равны,
следовательно,
Ошибка.
Попробуйте повторить позже
Около пятиугольника описана окружность, причем
Найдите радиус
описанной около этого пятиугольника окружности.
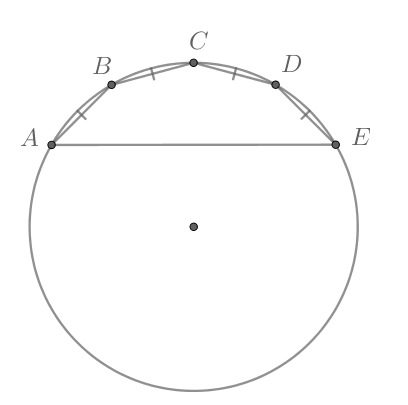
Рассмотрим картинку:

Т.к. равные хорды стягивают равные дуги, то меньшие полуокружности дуги
равны:
Следовательно, откуда
Значит, вписанный
Тогда, т.к. треугольник — вписанный, то
где
— радиус данной окружности. Следовательно:
Ошибка.
Попробуйте повторить позже
Около пятиугольника описана окружность, причем
Найдите высоту
треугольника
опущенную из вершины угла
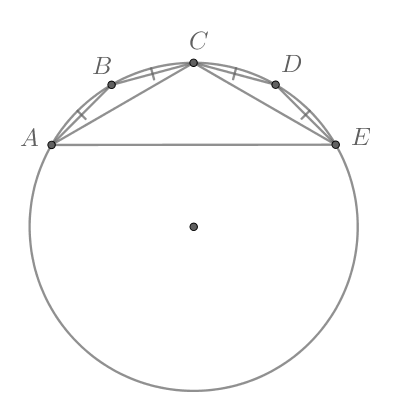
Рассмотрим картинку:
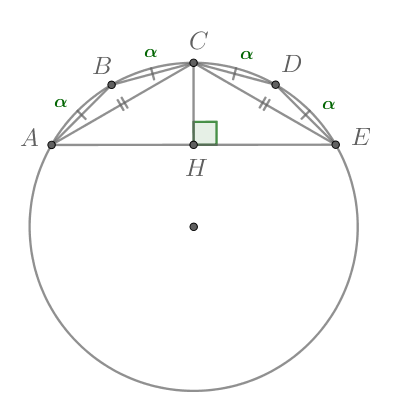
Т.к. равные хорды стягивают равные дуги, то меньшие полуокружности дуги
равны:
Следовательно, откуда
Тогда
Заметим, что треугольник — равнобедренный (
), следовательно,
— высота и медиана, то есть
Значит:
Ошибка.
Попробуйте повторить позже
Около пятиугольника описана окружность, причем
Радиус этой окружности равен
Найдите
радиус окружности, описанной около треугольника
где
— точка пересечения отрезков
и
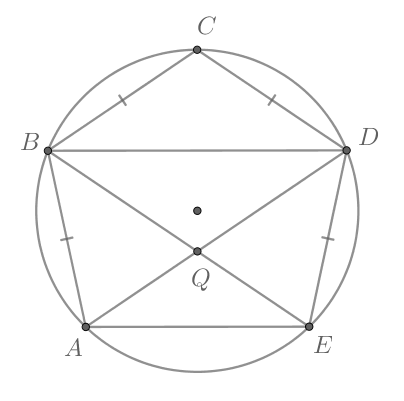
Рассмотрим картинку:
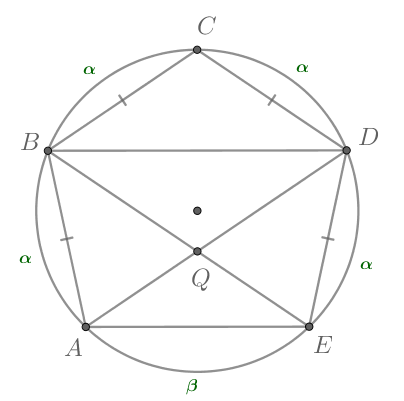
1) Т.к. равные хорды стягивают равные дуги, то меньшие полуокружности дуги
равны:
Пусть также
2)
Заметим, что градусная мера всей окружности равна следовательно,
откуда
Таким образом,
и
— односторонние углы при прямых
и
и секущей
Следовательно,
Аналогично доказывается, что
3) Значит, — параллелограмм (
). А в параллелограмме противоположные стороны равны,
следовательно,
То есть
— ромб.
4) Таким образом, Значит, и радиусы описанных около этих треугольников окружностей равны. Но радиус
описанной около треугольника
окружности равен радиусу описанной около пятиугольника
окружности.
Следовательно, ответ
Ошибка.
Попробуйте повторить позже
Восьмиугольник вписан в окружность. Найдите
Ответ дайте в
градусах.
и
— вписанные, тогда
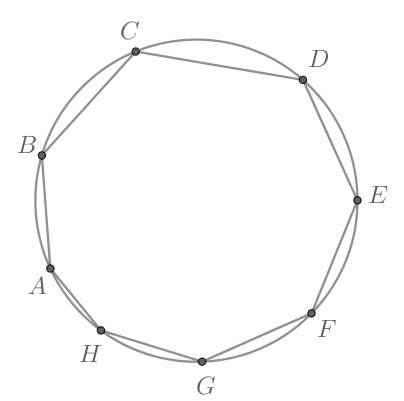
Назовём меньшую дугу малой. Аналогично назовём меньшие дуги
…,
малыми.
Каждую из дуг
можно разложить в сумму малых
дуг.
(сумму некоторых малых дуг). Остаётся понять, сколько раз в данную сумму войдёт
каждая малая дуга.
Например, войдёт трижды (среди слагаемых
она
не входит только в
).
Аналогично любая дуга войдёт в данную сумму трижды, следовательно,
где — градусная мера окружности.
Так как то
Ошибка.
Попробуйте повторить позже
Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции.
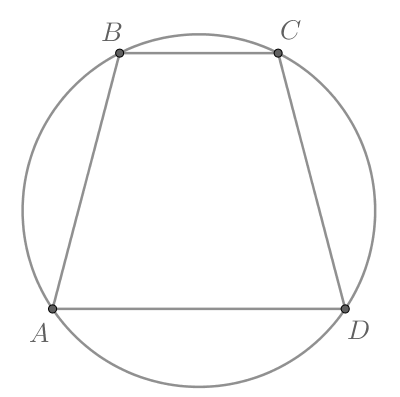
Так как трапеция вписана в окружность, то трапеция является равнобедренной, следовательно, . Средняя линия равна
полусумме оснований, следовательно,
Тогда
Ошибка.
Попробуйте повторить позже
Треугольники и
имеют равные углы
и
причем отрезок
не пересекает прямую
Найдите угол
если угол
равен
Ответ дайте в градусах.
Учитывая условие, рисунок будет выглядеть так:
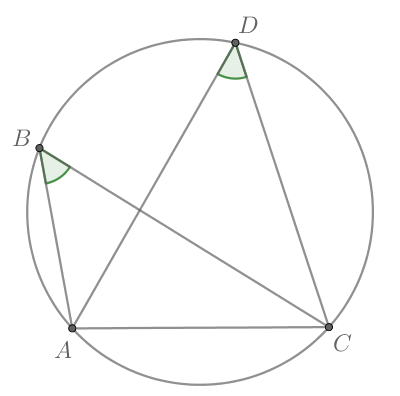
По признаку четырехугольник является вписанным, то есть около него можно описать окружность. Следовательно,
как вписанные углы, опирающиеся на одну дугу.
Заметим, что фраза ”отрезок не пересекает прямую” абсолютно не значит, что отрезок и прямая параллельны! Вот если бы это было сказано о двух прямых — другое дело. Если бы отрезок пересекал прямую, то картинка выглядела бы, например, так:
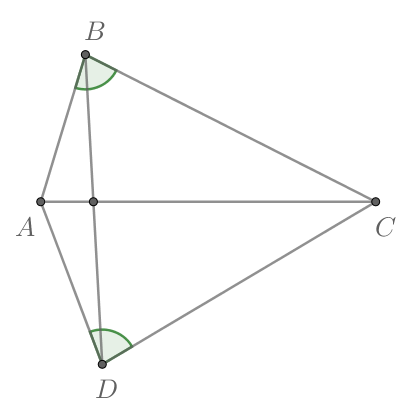
Ошибка.
Попробуйте повторить позже
В окружность вписан равносторонний треугольник Прямые, содержащие медианы этого треугольника, повторно пересекают
окружность в точках
и
Найдите площадь фигуры
если

Фигура, равная это шестиугольник
Заметим, что треугольник тоже правильный, причем равен треугольнику
Покажем, что
равен
так как
— биссектриса. Аналогично
Следовательно,
Аналогично доказывается, что
Следовательно, треугольник правильный. А так как радиус описанной около него окружности равен радиусу
окружности, описанной около
то треугольники равны.
Заметим, что — правильный шестиугольник.
У треугольника луч
содержит и биссектрису, и высоту, следовательно, треугольник
равнобедренный. А так
как его угол
равен
то он равносторонний. Аналогично доказывается, что и другие треугольники равносторонние
(
и т.д.).
Так как (опирается на диаметр), а
то
следовательно,
Следовательно,
Аналогично доказывается равенство остальных треугольников.
Следовательно, и
значит,
Тогда площадь правильного
шестиугольника равна
Ошибка.
Попробуйте повторить позже
Сторона тупоугольного треугольника
равна радиусу описанной около него окружности. Найдите тупой угол
Ответ
дайте в градусах.
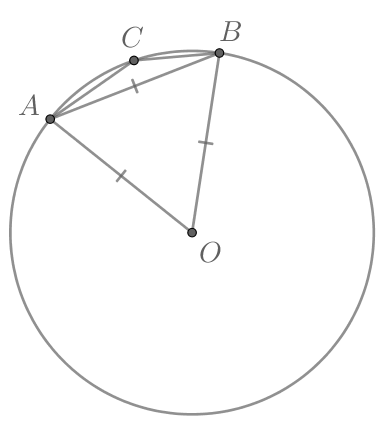
Треугольник равносторонний, следовательно,
Тогда большая дуга равна
Угол — вписанный угол, опирающийся на большую дугу
, следовательно, равен ее половине:
Ошибка.
Попробуйте повторить позже
Четырехугольник вписан в окружность. Угол
равен
угол
равен
Найдите угол
Ответ дайте
в градусах.
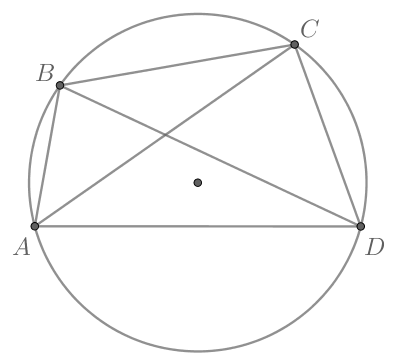
Так как вписанный угол равен половине дуги, на которую он опирается, то меньшая (см.рис.). Аналогично
меньшая дуга
(см.рис.). Следовательно, дуга
Значит
как вписанный и
опирающийся на дугу, равную
сам равен



