1.18 Окружность: вписанная в многоугольник или угол
Ошибка.
Попробуйте повторить позже
В четырёхугольник вписана окружность,
Найдите длину
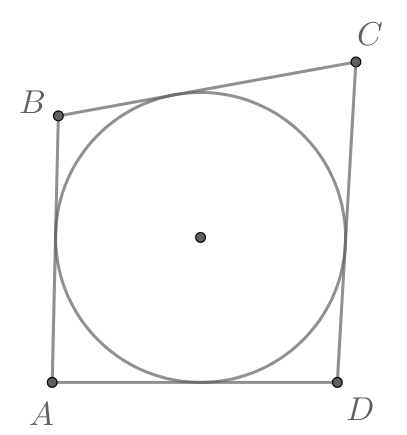
Если в четырёхугольник можно вписать окружность, то суммы его противоположных сторон равны: откуда
получаем
Ошибка.
Попробуйте повторить позже
В четырёхугольнике
точка
лежит на биссектрисах углов
и
Найдите
разность расстояний от точки
до
и от точки
до
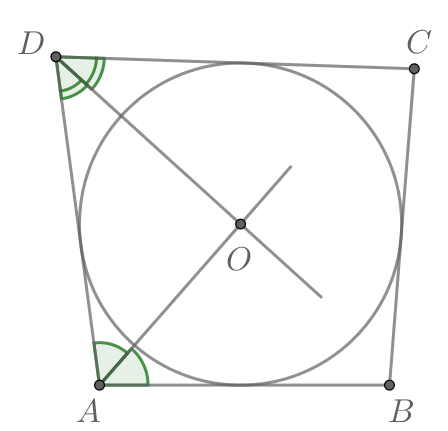
Если суммы противоположных сторон четырёхугольника равны, то в него можно вписать окружность, следовательно, в
можно вписать окружность.
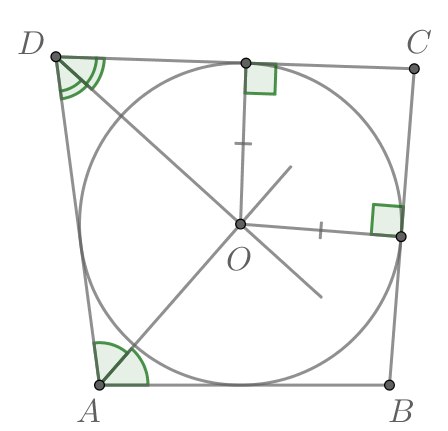
Так как в описанном четырёхугольнике биссектрисы всех его углов пересекаются в одной точке — центре вписанной в него
окружности, то — центр вписанной в
окружности, следовательно, расстояния от точки
до
и от точки
до
равны и их разность равна
Ошибка.
Попробуйте повторить позже
В треугольник вписана окружность с центром в точке
причем
Найдите
Ответ
дайте в градусах.
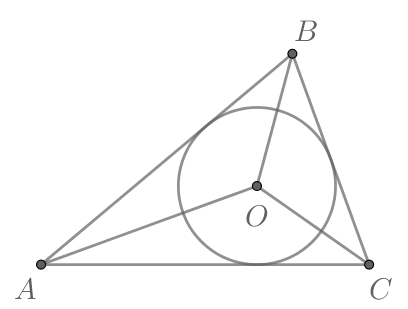
Так как центр вписанной окружности лежит на пересечении биссектрис углов треугольника, то — биссектрисы углов
соответственно.
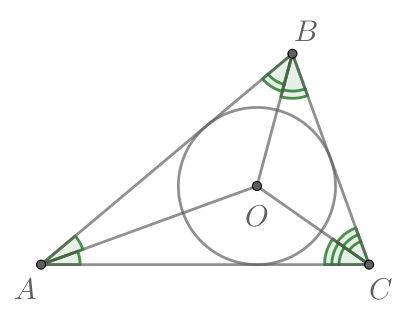
Тогда имеем:
Следовательно, искомый угол равен
Ошибка.
Попробуйте повторить позже
В треугольник вписана окружность радиуса Одна из сторон треугольника равна
а разность двух других равна
Найдите большую сторону этого треугольника.
1) Пусть в треугольнике
Таким образом, наибольшей стороной будет или
или
Т.к. отрезки касательных, проведенных из одной точки к окружности, равны, то
(где
— точки касания).
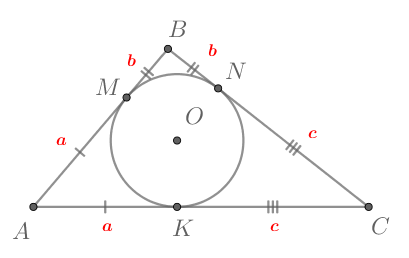
Таким образом, из условия следует, что
Решая систему из этих двух уравнений, находим,
что
2) Заметим, что полупериметр данного треугольника равен а площадь по формуле Герона
равна
Тогда по формуле (площадь равна полупериметру, умноженному на радиус вписанной окружности) имеем:
откуда Следовательно,
Значит, большая сторона равна
Ошибка.
Попробуйте повторить позже
Окружность касается стороны
и продолжений сторон
и
треугольника
Найдите длину
отрезка касательной к окружности
проведенной из точки
если периметр треугольника
равен

Рассмотрим рисунок:
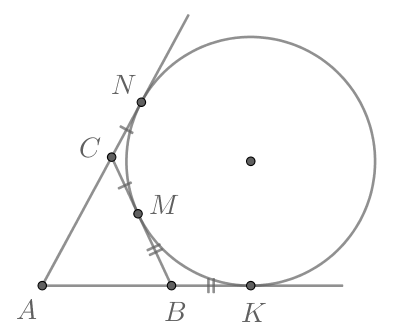
Т.к. отрезки касательных, проведенных из одной точки, равны, то
Таким образом,
периметр
Следовательно,
Ошибка.
Попробуйте повторить позже
Окружность вписана в угол равный
Найдите расстояние от вершины угла до центра этой окружности, если расстояние
между точками касания окружности и сторон угла равно
Обозначим точки касания окружности и сторон угла за и
Тогда известно, что
Пусть также
— центр
окружности. То есть необходимо найти
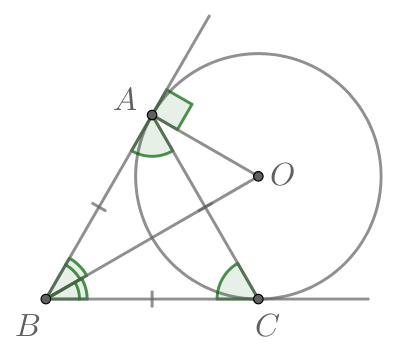
— радиус окружности, причем
(т.к.
— касательная, а радиус, проведенный в точку касания,
перпендикулярен касательной).
Рассмотрим треугольник он равнобедренный (
как отрезки касательных, проведенных из одной точки),
следовательно,
Таким образом, он равносторонний, следовательно,
Т.к. окружность вписана в угол, то ее центр лежит на биссектрисе этого угла, то есть Тогда из прямоугольного
треугольника
Ошибка.
Попробуйте повторить позже
В ромб со стороной вписана окружность. Найдите радиус этой окружности, если площадь ромба равна
Пусть дан ромб
— центр окружности, вписанной в этот ромб. Т.к. центр окружности, вписанной в
многоугольник, лежит на пересечении биссектрис его углов, то
— точка пересечения диагоналей ромба (т.к. они являются
биссектрисами углов ромба). Пусть
— точка касания окружности со стороной
Тогда
— радиус окружности.

Рассмотрим треугольники и
Они подобны по двум углам. Следовательно,
Т.к. площадь ромба равна полупроизведению диагоналей, то
Отсюда Следовательно,
Ошибка.
Попробуйте повторить позже
Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как Найдите
большую сторону этого четырехугольника, если известно, что его периметр равен 54.


Рассмотрим рисунок. Так как четырехугольник описан около окружности, то суммы его противоположных сторон равны.
Следовательно, четвертая сторона равна Тогда можно составить уравнение:
(большая сторона равна )
Ошибка.
Попробуйте повторить позже
Сторона ромба равна острый угол равен
Найдите радиус окружности, вписанной в этот ромб.
Для любого многоугольника, в который можно вписать окружность, верно где
— полупериметр, а
— радиус
вписанной окружности.
где — сторона ромба,
— его угол.
Следовательно,
Полупериметр ромба равен Тогда
Ошибка.
Попробуйте повторить позже
В треугольнике известно, что
угол
равен
Найдите радиус вписанной окружности.

Известно, что для любого треугольника
Здесь — полупериметр,
— радиус вписанной окружности.
В нашем случае получаем
Гипотенуза по теореме Пифагора равна
Следовательно, искомый радиус равен
Ошибка.
Попробуйте повторить позже
Боковые стороны равнобедренного треугольника равны основание равно
Найдите радиус вписанной окружности.
Известно, что для любого треугольника где
— полупериметр,
— радиус вписанной окружности. В нашем случае по
формуле Герона (полупериметр
)
Следовательно,
Ошибка.
Попробуйте повторить позже
В треугольник вписана окружность с центром в точке
причем
Найдите
треугольника
Ответ
дайте в градусах.
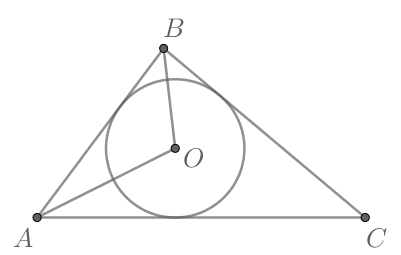
Так как центр вписанной окружности лежит на пересечении биссектрис углов треугольника, то — биссектрисы углов
соответственно. Тогда в треугольнике
имеем:
Следовательно, получаем
Значит, искомый угол равен
Ошибка.
Попробуйте повторить позже
Окружность вписана в угол равный
Найдите радиус этой окружности, если расстояние между точками касания
окружности и сторон угла равно
Обозначим точки касания окружности и сторон угла за и
Тогда известно, что
Пусть также
— центр
окружности.
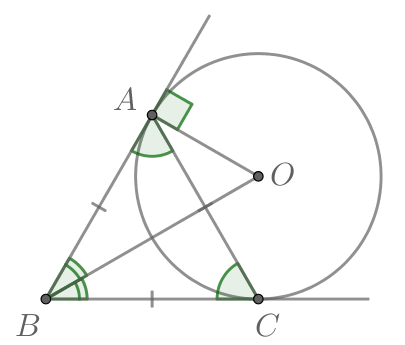
Тогда — радиус окружности, причем
(т.к.
— касательная, а радиус, проведенный в точку касания,
перпендикулярен касательной).
Рассмотрим треугольник он равнобедренный (
как отрезки касательных, проведенных из одной точки),
следовательно,
Таким образом, он равносторонний, следовательно,
Т.к. окружность вписана в угол, то ее центр лежит на биссектрисе этого угла, то есть Тогда из прямоугольного
треугольника
Ошибка.
Попробуйте повторить позже
Окружность вписана в угол равный
Найдите расстояние от вершины угла до центра этой окружности, если радиус этой
окружности равен
Обозначим одну из точек касания окружности и сторон угла за Пусть также
— центр окружности. То есть необходимо
найти
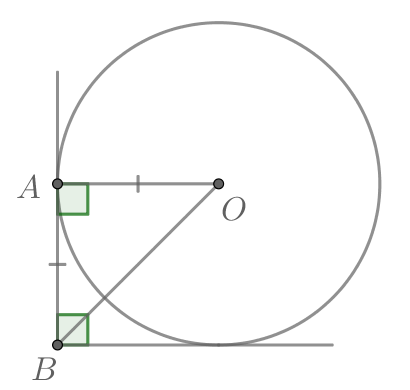
— радиус окружности, причем
(т.к.
— касательная, а радиус, проведенный в точку касания,
перпендикулярен касательной).
Т.к. окружность вписана в угол, то ее центр лежит на биссектрисе этого угла, то есть Тогда прямоугольный
треугольник
является равнобедренным, то есть
По теореме Пифагора:
Ошибка.
Попробуйте повторить позже
Окружность вписана в угол равный
причем
— точки касания окружности со сторонами этого угла. Найдите
площадь треугольника
если радиус этой окружности равен
Пусть — центр окружности.
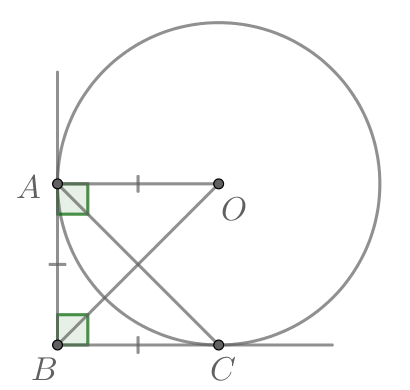
— радиус окружности, причем
(т.к.
— касательная, а радиус, проведенный в точку касания,
перпендикулярен касательной).
Т.к. окружность вписана в угол, то ее центр лежит на биссектрисе этого угла, то есть Тогда прямоугольный
треугольник
является равнобедренным, то есть
Т.к. отрезки касательных, проведенных из одной
точки к окружности, равны, то
Следовательно, площадь прямоугольного треугольника
равна
Ошибка.
Попробуйте повторить позже
Окружность вписана в угол равный
причем
— точки касания окружности со сторонами этого угла. Найдите
если радиус этой окружности равен
Пусть — центр окружности.
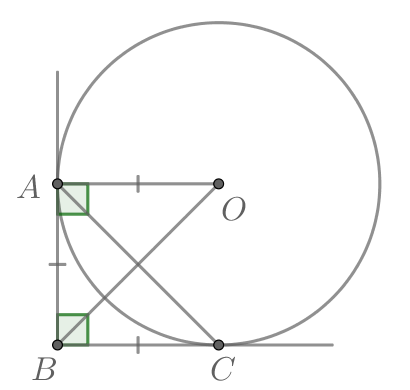
— радиус окружности, причем
(т.к.
— касательная, а радиус, проведенный в точку касания,
перпендикулярен касательной).
Т.к. окружность вписана в угол, то ее центр лежит на биссектрисе этого угла, то есть Тогда прямоугольный
треугольник
является равнобедренным, то есть
Т.к. отрезки касательных, проведенных из одной точки к
окружности, равны, то
Следовательно, по теореме Пифагора
Ошибка.
Попробуйте повторить позже
Около окружности, радиус которой равен описан прямоугольный треугольник, гипотенуза которого равна
Найдите
периметр этого треугольника.
Рассмотрим прямоугольный треугольник (
),
Пусть
— центр вписанной в него окружности. Пусть
также
— точки касания на сторонах
соответственно.
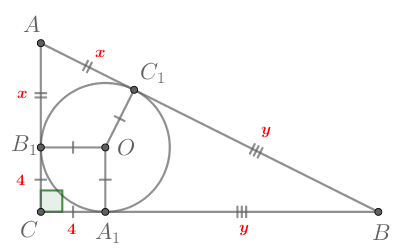
Т.к. отрезки касательных, проведенных из одной точки к окружности, равны, то
Заметим также, что радиусы и
перпендикулярны
и
соответственно (как радиусы, проведенные в точку
касания). Следовательно,
— прямоугольник (четырехугольник, имеющий три прямых угла). Но т.к. его смежные стороны
равны, то это – квадрат. Следовательно,
Тогда периметр треугольника равен:
Ошибка.
Попробуйте повторить позже
К окружности, вписанной в треугольник проведены три касательные, параллельные сторонам треугольника. Периметры
отсеченных треугольников равны
и
Найдите периметр треугольника


Рассмотрим рисунок. Пусть –= точки касания сторон треугольника
с окружностью.
— точки на
окружности, через которые проведены касательные параллельно сторонам треугольника. Получились треугольники
Пусть
Так как отрезки касательных, проведенных из одной точки к окружности, равны, то
Следовательно,
Аналогично для других треугольников:
Следовательно,
Ошибка.
Попробуйте повторить позже
Сторона правильного треугольника равна Найдите радиус окружности, вписанной в этот треугольник.

1 способ.
Центр вписанной окружности лежит на пересечении биссектрис. Так как треугольник правильный, то его биссектрисы также
являются высотами и медианами. Пусть — точка касания окружности со стороной
(то есть
— радиус).
Следовательно,
(как часть высоты) и
(как часть медианы, так как медианы точкой пересечения делятся в
отношении
считая от вершины).

Если то
следовательно,
тогда
2 способ.
Площадь правильного треугольника со стороной равна
Тогда по формуле
где
— полупериметр,
— радиус вписанной окружности, имеем:
Ошибка.
Попробуйте повторить позже
Радиус окружности, вписанной в правильный треугольник, равен Найдите сторону этого треугольника.
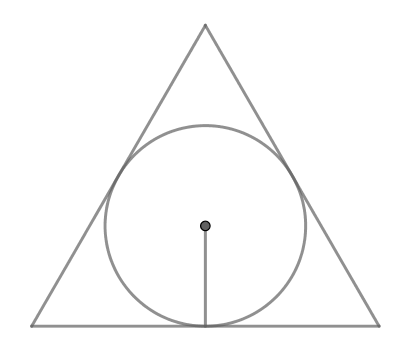
1 способ.
Центр вписанной окружности лежит на пересечении биссектрис. Так как треугольник правильный, то его биссектрисы также
являются высотами и медианами. Пусть — точка касания окружности со стороной
(то есть
— радиус).
Следовательно,
(как часть высоты) и
(как часть медианы, так как медианы точкой пересечения делятся в
отношении
считая от вершины).
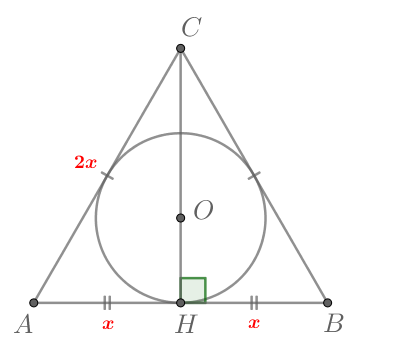
Если то
следовательно,
тогда
2 способ.
Площадь правильного треугольника со стороной равна
Тогда по формуле
где
— полупериметр,
—
радиус вписанной окружности, имеем:



