№18 из ЕГЭ 2024 —Каталог задач по ЕГЭ - Математика

Тема Задачи №18 из ЕГЭ прошлых лет

00 №18 из ЕГЭ 2024

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела задачи №18 из егэ прошлых лет

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#90052

Найдите все значения параметра $a,$ при каждом из которых система уравнений

{2x + 2ay+ a− 3= 0 x|y|+ 2x− 3= 0

имеет ровно два различных решения.

Источники: ЕГЭ 2024, основная волна, Дальний восток

Показать ответ и решение

Рассмотрим второе уравнение системы:

x|y|+ 2x− 3= 0 x(|y|+ 2)= 3

Заметим, что $|y|+2 ≥ 2.$ Тогда

x(|y|+ 2)= 3 2x = --6-- |y|+ 2

Тогда система имеет вид

( |{ 2x= − a(2y+ 1)+ 3 | --6-- ( 2x= |y|+ 2

Решим задачу графически в системе координат $yOx,$ где $y$ — абсцисса, $x$ — ордината. Тогда первое уравнение задает пучок прямых, проходящих через точку $(−0,5;1,5).$ Второе уравнение при $y ≥ 0$ задает часть гиперболы $3 x= y-+2$ и при $y < 0$ задает эту же кривую, но отраженную относительно оси $Ox.$

$yxx121−0=1 ---3- |y|+ 2$

Нам подходит только одно положение прямой, когда она касается гиперболы $-3-- x = y+ 2,$ при этом $y >0.$ Тогда уравнение

--3- = −a(y+ 0,5)+ 1,5 y +2 --6- = −a(2y+ 1)+3 y +2 6= − a(2y +1)(y+ 2)+3y +6 ( 2 ) a 2y + 5y+ 2 − 3y = 0 2ay2+ y(5a − 3)+ 2a= 0

квадратное и имеет один корень, то есть его дискриминант равен нулю:

D = 0 (5a− 3)2 − 16a2 = 0 2 2 25a − 30a + 9− 16a =0 3a2− 10a+ 3= 0 (3a − 1)(a− 3)= 0 ⌊ 1 ⌈a = 3 a =3

При $a= 3$ получаем, что

6y2+ 12y+ 6= 0 y2+ 2y+ 1= 0 2 (y+ 1) = 0 y = −1

Значит, такое значение параметра $a$ нам не подходит.

При $1 a= 3$ получаем, что

2y2 − 4y+ 2 =0 3 3 3 y2− 2y+ 1= 0 (y− 1)2 = 0 y =1

Тогда

3 3 x = y+-2 = 1+-2 = 1

Значит, касание происходит в точке $(1;1).$

Следовательно, нам подходит только ${ } a∈ 1 . 3$

Ответ:

${ } a ∈ 1 3$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#90055

Найдите все значения параметра $a,$ при каждом из которых система уравнений

{x + ay+ a− 2= 0 x|y|+ x− 2= 0

имеет ровно одно решение.

Источники: ЕГЭ 2024, основная волна, Дальний восток

Показать ответ и решение

Рассмотрим второе уравнение системы:

x|y|+ x− 2 =0 x(|y|+ 1)= 2

Заметим, что $|y|+1 ≥ 1.$ Тогда

x(|y|+ 1)= 2 x= --2-- |y|+1

Тогда система имеет вид

( |{ x= − a(y +1)+ 2 | --2-- ( x= |y|+ 1

Решим задачу графически в системе координат $yOx,$ где $y$ — абсцисса, $x$ — ордината. Тогда первое уравнение задает пучок прямых, проходящих через точку $(−1;2).$ Второе уравнение при $y ≥ 0$ задает часть гиперболы $2 x = y+-1$ и при $y < 0$ задает эту же кривую, но отраженную относительно оси $Ox.$

$yxx((121−0=1)2)1 ---2- |y|+ 1$

Пусть $a1$ и $a2$ — значения параметра $a,$ соответствующие положениям (1) и (2). Тогда нам подходят $a> a1$ или $a≤ a2.$

Положение (1): прямая $x = −a (y+ 1) +2 1$ касается гиперболы $x= --2-. y+ 1$ Тогда уравнение

--2- = −a1(y+ 1)+2 y +1 2 = −a1(y + 1)2+ 2y+ 2 2 a1y + 2a1y +a1− 2y =0 a1y2 +2y(a1− 1)+ a1 = 0

квадратное и имеет один корень, то есть его дискриминант равен нулю:

D = 0 4(a1− 1)2− 4a21 = 0 −2a + 1 =0 1 a1 = 1 2

Положение (2): прямая $x= −a2(y+ 1)+ 2$ горизонтальна, то есть $a2 = 0.$

Следовательно, нам подходят значения параметра

( 1 ) a ∈(−∞; 0]∪ 2;+∞ .

Ответ:

$a ∈(−∞; 0]∪(0,5;+∞ )$

Ошибка.
Попробуйте повторить позже

Задача 3#90056

Найдите все значения параметра $a,$ при каждом из которых система уравнений

{x +y = a ||2 || |y|= x − 2x

имеет ровно два различных решения.

Источники: ЕГЭ 2024, основная волна, Сибирь

Показать ответ и решение

Система из условия равносильна следующей:

(| y = − x+ a { [ 2 |( y = x −22x y = − x + 2x

Решим задачу графически. Пусть $S$ — множество точек плоскости $xOy,$ являющихся решением совокупности. Тогда необходимо найти такие $a,$ при которых прямая $y = −x+ a$ имеет 2 общие точки со множеством $S.$ Изобразим множество $S$ и ключевые положения прямой $y =− x+ a.$

$2 2 xyyy((1120 = =12))x− −x 2+x2x$

Нам подходят положения прямой $y = − x+ a$ ниже положения (1) или выше положения (2).

Положение (1): прямая $y = −x+ a1$ касается параболы $y = x2− 2x.$ Тогда уравнение

x2− 2x= − x+ a1 2 x − x− a1 = 0

имеет один корень, то есть его дискриминант равен нулю:

D1 = 0 1+ 4a1 = 0 1 a1 = −4

Положение (2): прямая $y = −x+ a2$ касается параболы $2 y = −x + 2x.$ Тогда уравнение

− x2+ 2x = −x +a2 x2− 3x+ a2 = 0

имеет один корень, то есть его дискриминант равен нулю:

D2 = 0 9− 4a2 = 0 a2 = 9 4

Следовательно, нам подходят значения параметра

( 1) ( 9 ) a∈ −∞; − 4 ∪ 4;+ ∞ .

Ответ:

$( ) ( ) a ∈ −∞; − 1 ∪ 9;+∞ 4 4$

Ошибка.
Попробуйте повторить позже

Задача 4#90058

Найдите все значения параметра $a,$ при каждом из которых система уравнений

{x +y = a ||2 || |y|= x − 4x

имеет ровно два различных решения.

Источники: ЕГЭ 2024, основная волна, Сибирь

Показать ответ и решение

Система из условия равносильна следующей:

(| y = − x+ a { [ 2 |( y = x −24x y = − x + 4x

$xyyy((1140 = =12))x−2−x24+x4x$

Нам подходят положения прямой $y = − x+ a$ ниже положения (1) или выше положения (2).

Положение (1): прямая $y = −x+ a1$ касается параболы $y = x2− 4x.$ Тогда уравнение

2 x −2 4x= − x+ a1 x − 3x− a1 = 0

имеет один корень, то есть его дискриминант равен нулю:

D1 = 0 9+ 4a1 = 0 a1 = − 9 4

Положение (2): прямая $y = −x+ a2$ касается параболы $y = −x2+ 4x.$ Тогда уравнение

− x2+ 4x = −x +a2 2 x − 5x+ a2 = 0

имеет один корень, то есть его дискриминант равен нулю:

D2 = 0 25− 4a2 = 0 25 a2 = 4

Следовательно, нам подходят значения параметра

( ) ( ) a ∈ −∞; − 9 ∪ 25;+∞ . 4 4

Ответ:

$( ) ( ) a ∈ −∞; − 9 ∪ 25;+∞ 4 4$

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	4

С помощью верного рассуждения получены верные значения параметра, но допущен недочет	3

С помощью верного рассуждения получен неверный ответ из-за вычислительной ошибки, при этом верно выполнены все шаги решения	2
ИЛИ
в решении верно найдены все граничные точки множества значений параметра, но неверно определены промежутки значений

В случае аналитического решения: задача верно сведена к набору решенных уравнений и неравенств с учетом требуемых ограничений	1
ИЛИ
в случае графического решения: задача верно сведена к исследованию взаимного расположения линий (изображены необходимые фигуры, учтены ограничения, указана связь исходной задачи с построенными фигурами)

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	4

Ошибка.
Попробуйте повторить позже

Задача 5#90060

Найдите все значения параметра $a,$ при каждом из которых система уравнений

{x +y = 2a ||2 || |y|= x + 2x

имеет ровно два различных решения.

Источники: ЕГЭ 2024, основная волна, Сибирь

Показать ответ и решение

Система из условия равносильна следующей:

(| y = − x+ 2a { [ 2 |( y = x +22x y = − x − 2x

$22 xyyy((11012==)) x−x+−2x2x$

Нам подходят положения прямой $y = − x+ 2a$ ниже положения (1) или выше положения (2).

Положение (1): прямая $y = −x+ 2a1$ касается параболы $y = x2+ 2x.$ Тогда уравнение

x2+2x = −x+ 2a1 2 x + 3x− 2a1 = 0

имеет один корень, то есть его дискриминант равен нулю:

D1 = 0 9+ 8a1 = 0 9 a1 = −8

Положение (2): прямая $y = −x+ 2a2$ касается параболы $2 y = −x − 2x.$ Тогда уравнение

−x2− 2x =− x+ 2a2 x2− x+ 2a2 = 0

имеет один корень, то есть его дискриминант равен нулю:

D2 = 0 1− 8a2 = 0 a2 = 1 8

Следовательно, нам подходят значения параметра

( 9) ( 1 ) a∈ −∞; − 8 ∪ 8;+ ∞ .

Ответ:

$( ) ( ) a ∈ −∞; − 9 ∪ 1;+∞ 8 8$

Ошибка.
Попробуйте повторить позже

Задача 6#90063

Найдите все значения параметра $a,$ при каждом из которых система уравнений

{y = |x− a|− 1 2 |y|+x − 2x = 0

имеет ровно четыре различных решения.

Источники: ЕГЭ 2024, основная волна, Центр

Показать ответ и решение

Преобразуем второе уравнение системы:

$pict$

Решим задачу графически. Пусть $S$ — множество точек плоскости $xOy,$ являющихся решением полученной системы. Графиком уравнения $y = |x− a|− 1$ является уголок, ветви которого направлены вверх, а вершина имеет координаты $(a;−1),$ то есть скользит по прямой $y = − 1.$ Нам нужно найти такие $a,$ при которых уголок имеет четыре общие точки со множеством $S.$

$xyyy1120((( = =123)))x−2−x22+x2x$

Если $ai$ — значение параметра, соответствующее положению $(i)$ уголка, то нам подходят $a∈ (a1;a2)∪ (a2;a3).$

Положение (1): левая ветвь уголка, задаваемая уравнением $yl = −x+ a1− 1,$ где $x ≤ a1,$ касается параболы $2 y = x − 2x.$ Тогда уравнение

2 x − 2x = −x+ a1− 1 x2− x+ 1− a1 = 0

имеет одно решение, следовательно,

D = 0 1− 4(1− a1)= 0 4a1− 3 = 0 a1 = 3 4

Тогда решением уравнения является $x= 1. 2$ Значит, касание прямой и параболы происходит при $3 a1 = 4,$ причем точка касания имеет координаты $( ) 1 3 2;− 4 .$ Эта точка принадлежит одновременно множеству $S$ и левой ветви уголка.

Положение (2): вершина уголка совпадает с вершиной параболы $2 y = x − 2x:$

(a2;− 1)= (1;−1) a2 = 1

Положение (3): правая ветвь уголка, задаваемая уравнением $yr = x− a3− 1,$ где $x ≥ a3,$ касается параболы $2 y = x − 2x.$ Тогда уравнение

2 x − 2x= x − a3 − 1 x2− 3x+ 1+ a3 = 0

имеет одно решение, следовательно,

D = 0 9− 4(1+ a3)= 0 5− 4a3 = 0 a3 = 5 4

Тогда решением уравнение является $x = 3. 2$ Значит, касание прямой и параболы происходит при $5 a3 = 4,$ причем точка касания имеет координаты $( ) 1 3 2;− 4 .$ Эта точка принадлежит одновременно множеству $S$ и правой ветви уголка.

Следовательно, нам подходят значения параметра

( ) ( ) a∈ 3;1 ∪ 1; 5 . 4 4

Ответ:

$( ) ( ) a ∈ 3;1 ∪ 1; 5 4 4$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#90066

Найдите все значения параметра $a,$ при каждом из которых система уравнений

{y = |x− a|− 4 2 4|y|+ x + 8x= 0

имеет ровно четыре различных решения.

Источники: ЕГЭ 2024, основная волна, Центр

Показать ответ и решение

Преобразуем второе уравнение системы:

$pict$

Решим задачу графически. Пусть $S$ — множество точек плоскости $xOy,$ являющихся решением полученной системы. Графиком уравнения $y = |x− a|− 4$ является уголок, ветви которого направлены вверх, а вершина имеет координаты $(a;−4),$ то есть скользит по прямой $y = − 4.$ Нам нужно найти такие $a,$ при которых уголок имеет четыре общие точки со множеством $S.$

$xx22 xyyy4−−0(((123==84))) −4-4+ −2 2xx$

Если $ai$ — значение параметра, соответствующее положению $(i)$ уголка, то нам подходят $a∈ (a1;a2)∪ (a2;a3).$

Положение (1): левая ветвь уголка, задаваемая уравнением $yl = −x+ a1− 4,$ где $x ≤ a1,$ касается параболы $2 y = x-+ 2x. 4$ Тогда уравнение

2 x- + 2x = −x +a1− 4 4 x2 +3x +4 − a1 = 0 4

имеет одно решение, следовательно,

D = 0 1 9− 4 ⋅4 ⋅(4− a1) 5+ a1 = 0 a1 = −5

Тогда решением уравнения является $x = −6.$ Значит, касание прямой и параболы происходит при $a1 = −5,$ причем точка касания имеет координаты $(− 6;− 3).$ Эта точка принадлежит одновременно множеству $S$ и левой ветви уголка.

Положение (2): вершина уголка совпадает с вершиной параболы $x2 y = 4 + 2x :$

(a2;−4)= (−4;−4) a2 = −4

Положение (3): правая ветвь уголка, задаваемая уравнением $yr = x− a3− 4,$ где $x ≥ a3,$ касается параболы $2 y = − x − 2x. 4$ Тогда уравнение

x2 − 4 − 2x = −x+ a3− 4 x2 4-+ x+ a3− 4= 0

имеет одно решение, следовательно,

D = 0 1 1− 4 ⋅4 ⋅(a3− 4) a3+ 3= 0 a3 = −3

Тогда решением уравнение является $x = −2.$ Значит, касание прямой и параболы происходит при $a3 = −3,$ причем точка касания имеет координаты $(− 2;− 3).$ Эта точка принадлежит одновременно множеству $S$ и правой ветви уголка.

Следовательно, нам подходят значения параметра

a∈ (− 5;− 4)∪(−4;−3).

Ответ:

$a ∈(−5;−4)∪ (−4;−3)$

Ошибка.
Попробуйте повторить позже

Задача 8#90067

Найдите все значения параметра $a,$ при каждом из которых система уравнений

{y = −|x − a|+ 1 2 |y|+x +2x = 0

имеет ровно четыре различных решения.

Источники: ЕГЭ 2024, основная волна, Центр

Показать ответ и решение

Преобразуем второе уравнение системы:

$pict$

Решим задачу графически. Пусть $S$ — множество точек плоскости $xOy,$ являющихся решением полученной системы. Графиком уравнения $y = −|x − a|+ 1$ является уголок, ветви которого направлены вниз, а вершина имеет координаты $(a;1),$ то есть скользит по прямой $y = 1.$ Нам нужно найти такие $a,$ при которых уголок имеет четыре общие точки со множеством $S.$

$xyyy1120(1(2(3 = =))) x−2x+2 2−x 2x$

Если $ai$ — значение параметра, соответствующее положению $(i)$ уголка, то нам подходят $a∈ (a1;a2)∪ (a2;a3).$

Положение (1): левая ветвь уголка, задаваемая уравнением $yl = x− a1+ 1,$ где $x ≤ a1,$ касается параболы $2 y = −x − 2x.$ Тогда уравнение

2 − x − 2x= x− a1+ 1 x2+ 3x+ 1− a1 = 0

имеет одно решение, следовательно,

D = 0 9− 4(1− a1)= 0 4a1+5 = 0 a1 = − 5 4

Тогда решением уравнения является $x = − 3 . 2$ Значит, касание прямой и параболы происходит при $5 a1 = − 4,$ причем точка касания имеет координаты $( ) 3 3 −2 ;4 .$ Эта точка принадлежит одновременно множеству $S$ и левой ветви уголка.

Положение (2): вершина уголка совпадает с вершиной параболы $2 y = −x − 2x :$

(a2;1)= (−1;1) a2 = −1

Положение (3): правая ветвь уголка, задаваемая уравнением $yr = −x +a3 +1,$ где $x ≥ a3,$ касается параболы $2 y = −x − 2x.$ Тогда уравнение

2 −x − 2x= − x+ a3+ 1 x2+ x+ 1+ a3 = 0

имеет одно решение, следовательно,

D = 0 1− 4(1+ a3)= 0 3+ 4a3 = 0 a3 = − 3 4

Тогда решением уравнение является $x = − 1. 2$ Значит, касание прямой и параболы происходит при $3 a3 = − 4,$ причем точка касания имеет координаты $( ) 1 3 −2 ;4 .$ Эта точка принадлежит одновременно множеству $S$ и правой ветви уголка.

Следовательно, нам подходят значения параметра

( ) ( ) a∈ − 5;−1 ∪ −1;− 3 . 4 4

Ответ:

$( ) ( ) a ∈ − 5;−1 ∪ −1;− 3 4 4$

Ошибка.
Попробуйте повторить позже

Задача 9#90068

Найдите все значения параметра $a,$ при каждом из которых система уравнений

{y = 4x+ a 2 |y|= x − 2x

имеет ровно два различных решения.

Источники: ЕГЭ 2024, основная волна, Сибирь

Показать ответ и решение

Преобразуем систему:

( y = 4x+ a |||{ 2 x[ − 2x2≥ 0 |||( y = x −22x y = − x + 2x

Решим задачу графически. Пусть $S$ — множество точек плоскости $xOy,$ являющихся решением совокупности при условии $x2− 2x ≥0.$ Тогда необходимо найти такие $a,$ при которых прямая $y = 4x+ a$ имеет 2 общие точки со множеством $S.$ Изобразим множество $S$ и ключевые положения прямой $y = 4x + a$ (обозначим ее за $l$ ).

$xyyy((((11201234==))))x−2x−2 2+x2x$

Если $ai$ — значение параметра, соответствующее положению $(i),$ то нам подходят

a∈ (− ∞;a1)∪ (a2;a3)∪(a4;+ ∞ ).

Положение (1): прямая $l$ касается параболы $2 y = x − 2x$ в точке с абсциссой больше 2. Тогда уравнение

x2− 2x =4x +a1 x2− 6x+ 9 =a1 +9 2 (x − 3) = a1+ 9

имеет единственное решение, если $a1+ 9 =0,$ то есть $a1 = −9.$ При этом значении параметра получаем, что точкой касания является точка $(3;3).$

Положение (2): точка $(2;0) ∈l,$ значит,

0= 4 ⋅2 + a2 a2 = −8

Положение (3): точка $(0;0) ∈l,$ значит,

0= 4 ⋅0 + a3 a3 = 0

Положение (4): прямая $l$ касается параболы $y = −x2+ 2x$ в точке с абсциссой меньше 0. Тогда уравнение

2 −x + 2x= 4x+ a4 x2 +2x +1 = −a4+ 1 (x +1)2 = 1− a4

имеет единственное решение, если $1 − a4 = 0,$ то есть $a4 = 1.$ При этом значении параметра получаем, что точкой касания является точка $(−1;−3).$

Следовательно, нам подходят значения параметра

a∈ (−∞; −9)∪ (− 8;0)∪ (1;+∞ ).

Ответ:

$a ∈(−∞; −9)∪ (−8;0) ∪(1;+ ∞ )$

Ошибка.
Попробуйте повторить позже

Задача 10#90071

Найдите все значения параметра $a,$ при каждом из которых система уравнений

{y = 4x+ a 2 2|y|= x − 4x

имеет ровно два различных решения.

Источники: ЕГЭ 2024, основная волна, Сибирь

Показать ответ и решение

Преобразуем систему:

(|y =4x + a |||| 2 ||{x⌊ − 4x ≥0 | y = 1x2− 2x ||||||⌈ 2 |( y = − 1x2 +2x 2

Решим задачу графически. Пусть $S$ — множество точек плоскости $xOy,$ являющихся решением совокупности при условии $x2− 4x ≥0.$ Тогда необходимо найти такие $a,$ при которых прямая $y = 4x+ a$ имеет 2 общие точки со множеством $S.$ Изобразим множество $S$ и ключевые положения прямой $y = 4x + a$ (обозначим ее за $l$ ).

$1122 xyyy((((11401234==)))) 2−x2x−+2x2x$

Если $ai$ — значение параметра, соответствующее положению $(i),$ то нам подходят

a∈ (− ∞;a1)∪ (a2;a3)∪(a4;+ ∞ ).

Положение (1): прямая $l$ касается параболы $y = 0,5x2− 2x$ в точке с абсциссой больше 4. Тогда уравнение

2 0,5x − 2x = 4x + a1 x2 − 12x =2a1 x2 − 12x +36 =2a1+ 36 2 (x − 6) = 2a1+ 36

имеет единственное решение, если $2a1+ 36= 0,$ то есть $a1 = −18.$ При этом значении параметра получаем, что точкой касания является точка $(6;6).$

Положение (2): точка $(4;0) ∈l,$ значит,

0= 4 ⋅4 + a2 a2 = −16

Положение (3): точка $(0;0) ∈l,$ значит,

0= 4 ⋅0 + a3 a3 = 0

Положение (4): прямая $l$ касается параболы $y = −0,5x2+2x$ в точке с абсциссой меньше 0. Тогда уравнение

2 − 0,5x + 2x= 4x+ a4 x2− 4x= − 8x− 2a4 x2+ 4x= − 2a4 2 x + 4x+ 4= 4− 2a4 (x+ 2)2 = 4− 2a4

имеет единственное решение, если $4 − 2a4 =0,$ то есть $a4 = 2.$ При этом значении параметра получаем, что точкой касания является точка $(−2;−6).$

Следовательно, нам подходят значения параметра

a∈ (−∞; −18)∪ (− 16;0)∪ (2;+∞ ).

Ответ:

$a ∈(−∞; −18)∪ (− 16;0)∪ (2;+ ∞)$

Ошибка.
Попробуйте повторить позже

Задача 11#90073

Найдите все значения параметра $a,$ при каждом из которых система уравнений

{ |y|− 4x− a= 0 2 x − 2x− y = 0

имеет ровно два различных решения.

Источники: ЕГЭ 2024, основная волна, Центр

Показать ответ и решение

Исключив $y$ из системы, получим уравнение

$pict$

Будем рассматривать параметр $a$ как переменную. Построим в системе координат $xOa$ множество $S$ решений совокупности. Если некоторая точка плоскости с координатами $(x ;a) 0 0$ принадлежит этому множеству $S,$ то для исходной задачи это означает, что если параметр $a$ принимает значение $a0,$ то $x0$ будет одним из решений совокупности. Нас просят найти все такие значения $a0$ параметра $a,$ при каждом из которых ровно две из точек вида $(x0;a0),$ где $x0 ∈ℝ,$ принадлежат множеству решений $S,$ изображенному на плоскости $xOa.$ Фактически это равносильно тому, что горизонтальная прямая $a= a0$ имеет ровно две точки пересечения с множеством $S.$

$xaaa12360== x−2−x26−x2x$

Видим, что нам подходят все положения горизонтальной прямой $a = a0$ выше положения, когда горизонтальная прямая проходит через вершину параболы $a = x2− 6x,$ то есть через точку $(3;− 9).$ Следовательно, нам подходят значения параметра $a > −9.$

Ответ:

$a ∈(−9;+∞ )$

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#90074

Найдите все значения параметра $a,$ при каждом из которых система уравнений

{|y|+|x|= a √----- y = x+ 4

имеет два различных решения.

Источники: ЕГЭ 2024, основная волна, Центр

Показать ответ и решение

При $a ≤0$ первое уравнение системы имеет не более одного решения, значит, и вся система тоже имеет не более одного решения. Тогда решим задачу графически при $a > 0.$ Исследуем первое уравнение:

$pict$

Таким образом, графиком этого уравнения является квадрат $ABCD$ с вершинами в точках $A (− a;0),$ $B (0;a),$ $C(a;0),$ $D(0;− a).$

Действительно, все стороны четырехугольника равны, значит, это ромб. Сторона $AB$ лежит на прямой $y = x+ a,$ сторона $BC$ лежит на прямой $y = −x+ a,$ угол между этими прямыми равен $∘ 90,$ следовательно, $ABCD$ — квадрат.

Нужно найти такие $a,$ при которых квадрат имеет две общие точки с графиком корня $y =√x-+-4.$

$√----- xyy(1(2(3ABCD110 =))) x +4$

Пусть $ai$ — значение параметра, соответствующее положению $(i).$ Тогда нам подходят

a∈ (a1;a2)∪ {a3}.

Положение (1): вершина $B (0;a1)$ находится в точке пересечения графика $y = √x+-4-$ с осью ординат. Значит,

√---- a1 = 0+ 4 a1 = 2

Положение (2): вершина $A (− a;0)$ находится в точке пересечения графика $√----- y = x+ 4$ с осью абсцисс. Значит,

√------- 0= − a2+ 4 a2 = 4

Положение (3): сторона $AB$ касается графика $√ ----- y = x+ 4.$ Сторона $AB$ задается уравнением $y = x+ a$ при $− a ≤ x≤ 0.$ Прямая касается графика корня, если система

( |{ √x+-4-=x + a3 1 |( 2√x-+4-= 1

имеет решения. Значит,

$pict$

Тогда

15 17 1 y = x +a3 = − 4-+-4 = 2.

Точка $( ) − 15; 1 4 2$ действительно лежит на отрезке $AB,$ так как её координаты обращают уравнение $y = x +a 3$ в верное равенство и $− a ≤x ≤ 0. 3$ Также она лежит на графике функции $y = √x-+-4,$ так как её координаты обращают это уравнение в верное равенство.

Следовательно, нам подходят значения параметра

{ } a ∈(2;4)∪ 17 4

Ответ:

${ } a ∈(2;4)∪ 17 4$

Ошибка.
Попробуйте повторить позже

Задача 13#90075

Найдите все значения параметра $a,$ при каждом из которых система уравнений

{|y|+|x|= a √----- y = x+ 9

имеет два различных решения.

Источники: ЕГЭ 2024, основная волна, Дагестан

Показать ответ и решение

$pict$

Нужно найти такие $a,$ при которых квадрат имеет две общие точки с графиком корня $y =√x-+-9.$

$√----- xyy(1(2(3ABCD12120 =))) x + 9$

Пусть $ai$ — значение параметра, соответствующее положению $(i).$ Тогда нам подходят

a∈ (a1;a2)∪ {a3}.

Положение (1): вершина $B (0;a1)$ находится в точке пересечения графика $√----- y = x+ 9$ с осью ординат. Значит,

a1 = √0+-9 a1 = 3

Положение (2): вершина $A (− a2;0)$ находится в точке пересечения графика $y = √x+-9-$ с осью абсцисс. Значит,

0= √−-a-+-9 2 a2 = 9

Положение (3): сторона $AB$ касается графика $y =√x-+-9.$ Сторона $AB$ задается уравнением $y = x+ a$ при $− a ≤ x≤ 0.$ Прямая касается графика корня, если система

(| √----- { x+ 9 =x + a3 |( -√-1---= 1 2 x +9

имеет решения. Значит,

$pict$

Тогда

y = x +a3 = − 35+ 37 = 1. 4 4 2

Точка $( ) − 35; 1 4 2$ действительно лежит на отрезке $AB,$ так как её координаты обращают уравнение $y = x +a3$ в верное равенство и $− a3 ≤x ≤ 0.$ Также она лежит на графике функции $√ ----- y = x+ 9,$ так как её координаты обращают это уравнение в верное равенство.

Следовательно, нам подходят значения параметра

{ } a ∈(3;9)∪ 37 4

Ответ:

${ } a ∈(3;9)∪ 37 4$

Ошибка.
Попробуйте повторить позже

Задача 14#90215

Найдите все значения параметра $a,$ при каждом из которых система уравнений

{x +y = a ||2 || |y|= x + 2x

имеет ровно два различных решения.

Источники: ЕГЭ 2024, основная волна, Центр

Показать ответ и решение

Система из условия равносильна следующей:

(| y = − x+ a { [ 2 |( y = x +22x y = − x − 2x

$22 xyyy((11012==)) x−x+−2x2x$

Нам подходят положения прямой $y = − x+ a$ ниже положения (1) или выше положения (2).

Положение (1): прямая $y = −x+ a1$ касается параболы $y = x2+ 2x.$ Тогда уравнение

x2+ 2x= − x+ a1 2 x + 3x− a1 = 0

имеет один корень, то есть его дискриминант равен нулю:

D1 = 0 9+ 4a1 = 0 9 a1 = −4

Положение (2): прямая $y = −x+ a2$ касается параболы $2 y = −x − 2x.$ Тогда уравнение

− x2− 2x = −x +a2 x2+ x+ a2 = 0

имеет один корень, то есть его дискриминант равен нулю:

D2 = 0 1− 4a2 = 0 a2 = 1 4

Следовательно, нам подходят значения параметра

( 9) ( 1 ) a∈ −∞; − 4 ∪ 4;+ ∞ .

Ответ:

$( ) ( ) a ∈ −∞; − 9 ∪ 1;+∞ 4 4$

Ошибка.
Попробуйте повторить позже

Задача 15#2137

Найдите все значения параметра $a$ , при которых уравнение

2 (|x +2|+ |x − a|) − 5⋅(|x+ 2|+ |x− a|)+3a(5− 3a)= 0

имеет ровно два различных решения.

Источники: ЕГЭ 2014, резерв

Показать ответ и решение

1) Сделаем замену $y = |x+ 2|+|x− a|$ . Тогда уравнение примет вид

2 y − 5y+ 3a(5− 3a)= 0.

Получили квадратное уравнение. Для того, чтобы изначальное уравнение относительно $x$ имело решения, полученное уравнение относительно $y$ должно иметь решения, то есть его дискриминант должен быть неотрицательным. Найдем дискриминант:

D =25 − 60a+ 36a2 = (6a− 5)2 ≥0.

Таким образом, дискриминант для любого $a$ будет неотрицательным. Имеем корни:

$pict$

2) Таким образом, исходное уравнение равносильно совокупности

[ |x +2|+ |x− a|=3a |x +2|+ |x− a|=5 − 3a

Оба уравнения в данной совокупности имеют вид

|x+ 2|+ |x − a|= t

Здесь $t$ — некоторое выражение, зависящее от $a.$ Исследуем такое уравнение.

График функции $f(x) =|x+ 2|+ |x− a|$ представляет собой корыто, ветви которого имеют наклон $± 2,$ а дно находится на высоте $|2 +a|:$

$xy−aattt2=== −2x|22+x+−a2|2−+aa$

(числа $− 2$ и $a$ могут поменяться местами)

Следовательно, при $t> |2+ a|$ уравнение $t= f(x)$ имеет два решения, при $t= |2+ a|$ имеет бесконечно много решений при $a⁄= − 2$ и одно решение при $a = −2,$ при $t< |2+ a|$ не имеет решений. Следовательно, если $t= 3a$ и $t= 5 − 3a$ — разные прямые, то необходимо

⌊( ⌊ { |{ −[3a <2 +a < 3a 3a >|2+ a| ||| 2+ a >5 − 3a ⌊ ||| {5− 3a <|2+ a| |||( [2+ a <3a − 5 ⌈a >1 |⌈ 3a <|2+ a| ⇔ ||(|{ 2+ a >3a ⇔ a < 3 5− 3a >|2+ a| |⌈ 2+ a <− 3a 4 |( 3a− 5< 2+ a <5 − 3a

Если же прямые $t= 3a$ и $t= 5− 3a$ совпадают, то $3a= 5 − 3a,$ следовательно, $5 a = 6.$ Тогда имеем:

|2+ a|= 25 > 2,5 =3a 6

Следовательно, при $a= 5 6$ прямые $t= 3a$ и $t= 5− 3a$ находятся ниже дна корыта и исходное уравнение не имеет корней.

Тогда исходное уравнение имеет ровно два различных решения при

( ) a∈ −∞; 3 ∪ (1;+∞ ) 4

Ответ:

$( 3) −∞; 4 ∪(1;+∞ )$

Ошибка.
Попробуйте повторить позже

Задача 16#91276

На серединах сторон $AB,$ $BC$ и $AC$ треугольника $ABC$ с тупым углом $A$ отмечены точки $C1,$ $A1$ и $B1$ соответственно.

a) Докажите, что окружность, описанная около треугольника $AB1C1,$ проходит через отличную от $A1$ точку пересечения описанных окружностей треугольников $A1B1C$ и $A1BC1.$

б) Известно, что $AB = AC = 10$ и $BC = 16.$ Найдите радиус окружности, описанной около треугольника с вершинами в центрах вписанных окружностей треугольников $AB C , 1 1$ $A B C 1 1$ и $A BC . 1 1$

Источники: ЕГЭ 2024, резервный день

Показать ответ и решение

а) Пусть $O$ — отличная от $A1$ точка пересечения окружностей, описанных около треугольников $A1B1C$ и $A1BC1.$ Тогда имеем:

$pict$

$PIC$

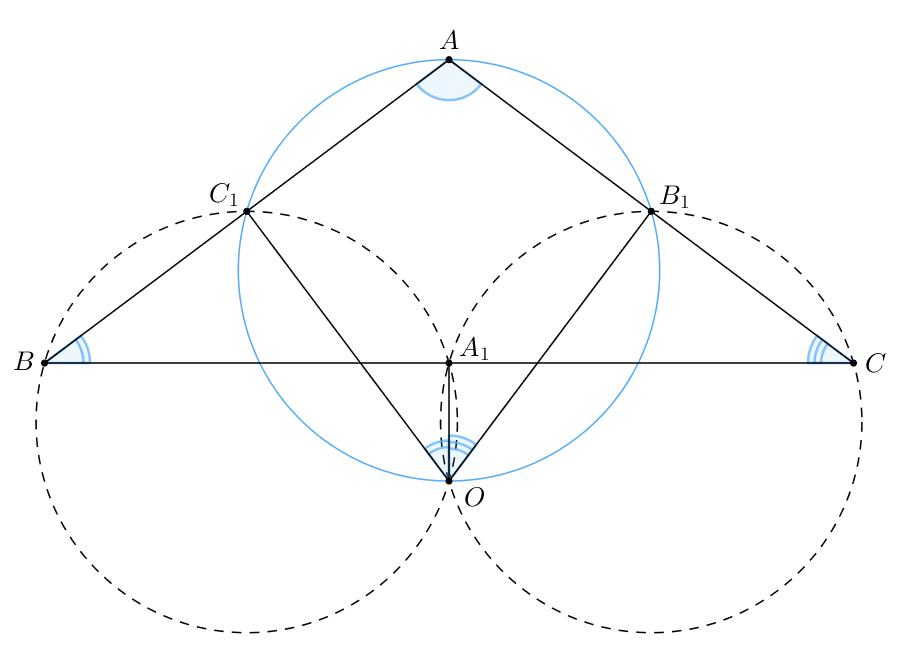
Тогда

∠A1OB1 + ∠A1OC1 = ∠C1OB1

Значит, в четырехугольнике $AB OC : 1 1$

∠B1AC1 + ∠C1OB1 = ∠B1AC1 + ∠A1CB1 + ∠A1BC1 = 180∘

Таким образом, сумма противоположных углов четырехугольника $AB1OC1$ равна $∘ 180 ,$ следовательно, он вписанный. Значит, описанная окружность треугольника $AB C 1 1$ проходит через точку $O$ пересечения описанных окружностей треугольников $A1B1C$ и $A1BC1.$

б) Пусть $IA$ — центр вписанной окружности треугольника $AB1C1,$ $IB$ — центр вписанной окружности треугольника $A1BC1,$ $IC$ — центр вписанной окружности треугольника $A1B1C.$

Кроме того, $A1B1,$ $B1C1,$ $A1C1$ — средние линии треугольника $ABC.$ Тогда имеем:

$pict$

$PIC$

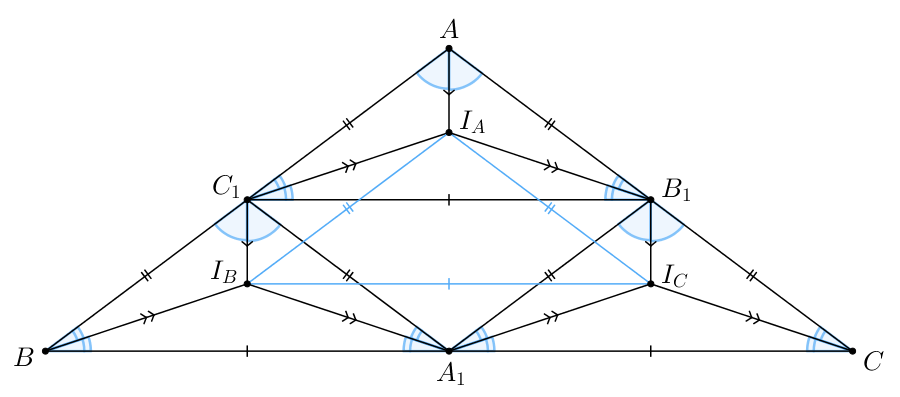
Значит, треугольники $AB1C1,$ $C1A1B,$ $B1CA1$ равны по трем сторонам. В равных треугольниках соответственные элементы равны, поэтому $AIA = C1IB$ и $∠IAAC1 = ∠IBC1B.$ Тогда отрезки $AIA$ и $C1IB$ равны и параллельны. Следовательно, $AIAIBC1$ — параллелограмм. Тогда

IAIB = AC1 = 1AB. 2

Аналогично докажем, что $IAIC = 1AC 2$ и $IBIC = 1BC. 2$

Тогда треугольник $IAIBIC$ подобен треугольнику $ABC$ с коэффициентом $1 2 .$ Значит, радиус описанной окружности $△ IAIBIC$ в 2 раза меньше радиуса описанной окружности $△ ABC.$

По условию в треугольнике $ABC$ стороны $AB$ и $AC$ равны, то есть он равнобедренный. Косинус угла при основании равнобедренного треугольника равен отношению половины основания к боковой стороне, поэтому

1 cos∠B = 2BC-= -8 = 4. AB 10 5

Тогда получаем

∘ ------ ∘------2--- 16 3 sin ∠B = 1 − cos ∠B = 1− 25 = 5.

Значит, по теореме синусов для треугольника $ABC$ с радиусом $R$ описанной окружности:

--AC--= 2R sin∠B R = -10- 2 ⋅ 35 25 R = -3

Тогда радиус описанной окружности треугольника $IAIBIC$ равен $25 r =-6 .$

Ответ:

б) $25 6$

Критерии оценки


Содержание критерия	Балл

Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б)	3

Обоснованно получен верный ответ в пункте б)	2
ИЛИ
имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки

Имеется верное доказательство утверждения пункта а),	1
ИЛИ
при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,
ИЛИ
обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	3

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 17#91277

Найдите все значения параметра $a,$ при каждом из которых уравнение

( 2)3 ( 2)2 3|x−a| 2|x−a| 1− (x + a+ 1) − 1− (x +a + 1) = 2 − 2

имеет хотя бы один корень.

Источники: ЕГЭ 2024, резервный день, Центр

Показать ответ и решение

( 2)3 ( 2)2 3|x−a| 2|x−a| 1− (x + a+ 1) − 1− (x +a + 1) = 2 − 2

Пусть $u = 1− (x + a+ 1)2,$ $v = 2|x−a|.$ Тогда уравнение примет вид

3 2 3 2 u − u = v − v .

Заметим, что $(x+ a+ 1)2 ≥ 0$ и $|x− a|≥0.$ Тогда

$pict$

Исследуем функцию

f(t)= t3 − t2 = t2(t− 1).

Если $t ≤1,$ то $f(t)≤ 0.$ Если $t≥ 1,$ то $f(t)≥ 0.$

Тогда так как $u ≤1$ и $v ≥ 1,$ то получаем, что $f(u)≤ 0$ и $f(v)≥ 0,$ то есть

0 ≥f(u)= u3− u2 = v3− v2 = f(v)≥ 0.

Значит, равенство достигается только при $f(u)= 0= f(v).$ Таким образом,

[ (|| u= 0 {f(u)= 0 {u2(u− 1)= 0 ||{ u= 1 ⇔ 2 ⇔ | [ f(v)= 0 v (v − 1) =0 |||( v = 0 v = 1

Мы знаем, что $v ≥ 1,$ поэтому

([ ([ |{ u= 0 |{ 1 − (x+ a +1)2 = 0 u= 1 ⇔ 1 − (x+ a +1)2 = 1 |(v = 1 |(2|x− a| = 1

Решим последнее уравнение системы:

|x− a| 2 = 1 2|x−a| = 20 |x− a|=0 x− a= 0 x =a

Тогда получаем

( ⌊ (|{ [(2a +1)2 = 1 |||{ |a= 0 (2a +1)2 = 0 ⇔ ⌈a= −1 |( ||| a= −0,5 x= a ( x= a

Таким образом, исходное уравнение имеет хотя бы один корень при

a ∈{− 1;− 0,5;0}.

Ответ:

$a ∈{− 1;− 0,5;0}$

Ошибка.
Попробуйте повторить позже

Задача 18#91278

Найдите все значения параметра $a,$ при каждом из которых уравнение

( 2)3 ( 2)2 3|x+2a| 2|x+2a| 1− (x− 2a+ 1) − 1− (x− 2a+ 1) = 2 − 2

имеет хотя бы один корень.

Источники: ЕГЭ 2024, резервный день, Центр

Показать ответ и решение

( 2)3 ( 2)2 3|x+2a| 2|x+2a| 1− (x− 2a+ 1) − 1− (x− 2a+ 1) = 2 − 2

Пусть $u = 1− (x − 2a+ 1)2,$ $v = 2|x+2a|.$ Тогда уравнение примет вид

3 2 3 2 u − u = v − v .

Заметим, что $(x− 2a+ 1)2 ≥ 0$ и $|x + 2a|≥ 0.$ Тогда

$pict$

Исследуем функцию

f(t)= t3 − t2 = t2(t− 1).

Если $t ≤1,$ то $f(t)≤ 0.$ Если $t≥ 1,$ то $f(t)≥ 0.$

Тогда так как $u ≤1$ и $v ≥ 1,$ то получаем, что $f(u)≤ 0$ и $f(v)≥ 0,$ то есть

0 ≥f(u)= u3− u2 = v3− v2 = f(v)≥ 0.

Значит, равенство достигается только при $f(u)= 0= f(v).$ Таким образом,

[ (|| u= 0 {f(u)= 0 {u2(u− 1)= 0 ||{ u= 1 ⇔ 2 ⇔ | [ f(v)= 0 v (v − 1) =0 |||( v = 0 v = 1

Мы знаем, что $v ≥ 1,$ поэтому

( [ ( [ |{ u =0 |{ 1− (x− 2a+ 1)2 =0 u =1 ⇔ 1− (x− 2a+ 1)2 =1 |( v = 1 |( 2|x+2a| =1

Решим последнее уравнение системы:

|x+2a| 2 =1 2|x+2a| = 20 |x+ 2a|= 0 x+ 2a =0 x= − 2a

Тогда получаем

( ⌊ (|{[(−4a +1)2 = 1 |||{ |a= 0 (−4a +1)2 = 0 ⇔ ⌈a= 0,5 |( ||| a= 0,25 x = −2a ( x= −2a

Таким образом, исходное уравнение имеет хотя бы один корень при

a∈ {0;0,25;0,5}.

Ответ:

$a ∈{0;0,25;0,5}.$

Ошибка.
Попробуйте повторить позже

Задача 19#91279

Найдите все значения параметра $a,$ при каждом из которых уравнение

(2 +|x+ a|)3− (2+ |x +a|)2 = (3 − x2 − 2ax − 2a2)3− (3− x2− 2ax − 2a2)2

имеет хотя бы один корень.

Источники: ЕГЭ 2024, резервный день, Центр

Показать ответ и решение

(2 +|x+ a|)3− (2+ |x +a|)2 = (3 − x2 − 2ax − 2a2)3− (3− x2− 2ax − 2a2)2

Пусть $u = 2+ |x +a|,$ $v = 3 − x2 − 2ax − 2a2.$ Тогда уравнение примет вид

3 2 3 2 u − u = v − v .

Заметим, что так как $|x+ a|≥0,$ то

u= 2+ |x + a|≥2,

Исследуем функцию

f(t)= t3− t2.

Найдем ее производную:

( ) f′(t)= t3 − t2 ′ =3t2− 2t= t(3t− 2)

Найдем нули производной:

⌊ t= 0, ⌈ 2 t= 3.

Тогда имеем:

$t0+−+f2′(t) : 3$

Значит, $t= 0$ — точка максимума, $2 t= 3$ — точка минимума. При этом

$pict$

Можем нарисовать эскиз графика функции $f(t) :$

$ty022 3$

По графику видно, что все значения, которые функция $f(t)$ принимает на промежутке $[2;+∞ ),$ она принимает ровно один раз. Значит, так как $u≥ 2,$ то верно следующее:

f(u)= f(v) ⇔ u = v.

Тогда заметим, что

2 2 v = 3− x − 2ax − 2a = = 3− (x2 +2ax +a2)− a2 = =3 − a2 − |x+ a|2.

Следовательно,

2+ |x+ a|= 3− a2− |x + a|2 |x+ a|2+ |x+ a|− 1+ a2 = 0

Мы получили квадратное уравнение относительно $|x+ a|.$ Нам нужно найти такие значения параметра $a,$ при которых это квадратное уравнение имеет хотя бы один неотрицательный корень.

Пусть $z = |x+ a|≥ 0.$ Рассмотрим функцию

g(z)= z2+ z+ (a2− 1).

Графиком этой квадратичной функции является парабола с вершиной в точке

zверш. =-−1-= − 1. 2 ⋅1 2

Тогда график функции $g(z)$ выглядит так:

$zy0$

Функция $g(z)$ должна иметь хотя бы один неотрицательный корень, следовательно,

g(0) ≤0 a2− 1≤ 0 a2 ≤ 1 −1 ≤a ≤ 1

Ответ:

$a ∈[−1;1]$

Ошибка.
Попробуйте повторить позже

Задача 20#91280

Найдите все значения параметра $a,$ при каждом из которых уравнение

(3 +2|x+ a|)3− (3+ 2|x +a|)2 = (7 − x2 − 2ax − 2a2)3− (7 − x2 − 2ax − 2a2)2

имеет хотя бы один корень.

Источники: ЕГЭ 2024, резервный день, Центр

Показать ответ и решение

(3 +2|x+ a|)3− (3+ 2|x +a|)2 = (7 − x2 − 2ax − 2a2)3− (7 − x2 − 2ax − 2a2)2

Пусть $u = 3+ 2|x +a|,$ $v = 7− x2− 2ax− 2a2.$ Тогда уравнение примет вид

3 2 3 2 u − u = v − v .

Заметим, что так как $2|x + a|≥ 0,$ то

u = 3+ 2|x +a|≥ 3

Исследуем функцию

f(t)= t3− t2.

Найдем ее производную:

( ) f′(t)= t3 − t2 ′ =3t2− 2t= t(3t− 2)

Найдем нули производной:

⌊ t= 0, ⌈ 2 t= 3.

Тогда

$t0+−+f2′(t) : 3$

Значит, $t= 0$ — точка максимума, $2 t= 3$ — точка минимума. При этом

$pict$

Можем нарисовать эскиз графика функции $f(t) :$

$ty032 3$

По графику видно, что все значения, которые функция $f(t)$ принимает на промежутке $[3;+∞ ),$ она принимает ровно один раз. Значит, так как $u≥ 3,$ то верно следующее: