Окружность, вписанная в многоугольник или угол

Окружность называется вписанной в выпуклый многоугольник/угол, если она касается всех сторон этого многоугольника/угла.
Тогда многоугольник/угол называется описанным около окружности.
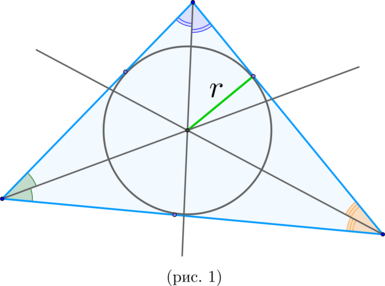
\(\blacktriangleright\) В любой треугольник можно вписать окружность. Ее центр лежит на пересечении биссектрис треугольника (рис. 1).
Площадь описанного треугольника ищется по формуле \[{\Large{S_{\triangle}=p\cdot r}},\]
где \(p\) – полупериметр.
\(\blacktriangleright\) Если в прямоугольный треугольник вписана окружность, \(a, b\) – катеты, \(c\) – гипотенуза, \(r\) – радиус этой окружности, то верна формула: \[{\large{r=\dfrac{a+b-c}2}}\] 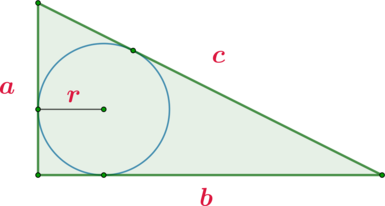
\(\blacktriangleright\) Если в выпуклый четырехугольник можно вписать окружность, то суммы его противоположных сторон равны.
И наоборот: если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность (рис. 2).
Центр вписанной окружности лежит на пересечении биссектрис углов.
Площадь описанного четырехугольника ищется по формуле
\[{\large{S_{\text{опис.4-к}}=p\cdot r}},\]
где \(p\) – полупериметр.

\(\blacktriangleright\) Если в параллелограмм вписана окружность, то он – ромб (рис. 3).
\(\blacktriangleright\) Если в прямоугольник вписана окружность, то он – квадрат (рис. 4).
\(\blacktriangleright\) Если в угол вписана окружность, то ее центр лежит на биссектрисе этого угла (рис. 5).

Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как \(2:3:6\). Найдите большую сторону этого четырехугольника, если известно, что его периметр равен \(54\).
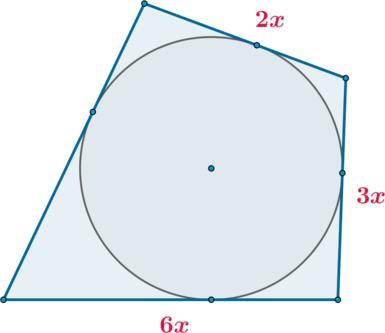
Рассмотрим рисунок. Так как четырехугольник описан около окружности, то суммы его противоположных сторон равны. Следовательно, четвертая сторона равна \((2x+6x)-3x=5x\). Тогда можно составить уравнение: \[2x+3x+6x+5x=54\quad\Leftrightarrow\quad 6x=20,25\] (большая сторона равна \(6x\))
В четырёхугольник \(ABCD\) вписана окружность, \(AB = 3,5\), \(AD = 4\), \(BC = 6,5\). Найдите длину \(CD\).
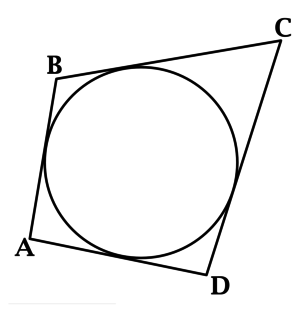
Если в четырёхугольник можно вписать окружность, то суммы его противоположных сторон равны:
\(AB + CD = AD + BC\), откуда получаем \(3,5 + CD = 4 + 6,5\), значит, \(CD = 7\).
В треугольник \(ABC\) вписана окружность с центром в точке \(O\), причем \(\angle AOB=110^\circ\). Найдите \(\angle C\) треугольника \(ABC\). Ответ дайте в градусах.
Т.к. центр вписанной окружности лежит на пересечении биссектрис углов треугольника, то \(AO, BO\) – биссектрисы углов \(A, B\) соответственно.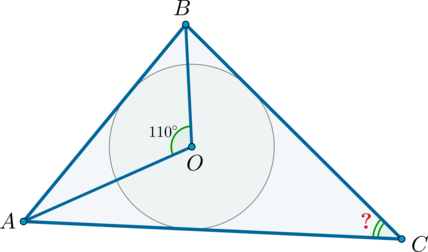
Следовательно, \(\angle BAO+\angle
ABO=180^\circ-110^\circ=70^\circ\).
Также \(\angle A+\angle B=2\cdot (\angle BAO+\angle ABO)=140^\circ\), следовательно, \(\angle C=180^\circ-(\angle A+\angle
B)=180^\circ-140^\circ=40^\circ\).
Боковые стороны равнобедренного треугольника равны \(5\), основание равно \(6\). Найдите радиус вписанной окружности.
Известно, что для любого треугольника \(S_{\triangle}=p\cdot r\), где \(p\) – полупериметр, \(r\) – радиус вписанной окружности.
В нашем случае по формуле Герона (полупериметр \(p=8\)) \(S_{\triangle}=\sqrt{8\cdot 3\cdot 3\cdot 2}=4\cdot 3=12\). Следовательно, \[r=\dfrac Sp=\dfrac{12}{0,5(5+5+6)}
= 1,5\]
Около окружности, радиус которой равен \(3\), описан многоугольник, периметр которого равен \(20\). Найдите его площадь. 
Так как для любого многоугольника, в который можно вписать окружность, верно \(S=p\cdot r\), где \(p\) – полупериметр, а \(r\) – радиус вписанной окружности, то \[S=\dfrac{20}2\cdot 3=30\]
Сторона правильного треугольника равна \(\sqrt3\). Найдите радиус окружности, вписанной в этот треугольник.
1 способ.
Центр вписанной окружности лежит на пересечении биссектрис. Так как треугольник правильный, то его биссектрисы также являются высотами и медианами. Пусть \(H\) – точка касания окружности со стороной \(AB\) (то есть \(OH\) – радиус). Следовательно, \(OH\perp AB\) (как часть высоты) и \(OH=\frac13CH\) (как часть медианы, так как медианы точкой пересечения делятся в отношении \(2:1\), считая от вершины).
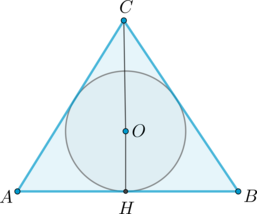
Если \(AC=2x=\sqrt3\), то \(AH=x\), следовательно, \(CH=\sqrt{4x^2-x^2}=x\sqrt3\), тогда \[OH=\dfrac13\cdot CH=\dfrac13\cdot \sqrt3\cdot \dfrac{\sqrt3}2=0,5\]
2 способ.
Площадь правильного треугольника со стороной \(a\) равна \(S=\dfrac{\sqrt3}4a^2\). Тогда по формуле \(S=p\cdot r\), где \(p\) – полупериметр, \(r\) – радиус вписанной окружности, имеем: \[r=\dfrac Sp=\dfrac{\frac{\sqrt3}4\cdot (\sqrt3)^2}{0,5(\sqrt3+\sqrt3+\sqrt3)}
=0,5\]
Радиус окружности, вписанной в правильный треугольник, равен \(\dfrac{\sqrt3}6\). Найдите сторону этого треугольника.

1 способ.
Центр вписанной окружности лежит на пересечении биссектрис. Так как треугольник правильный, то его биссектрисы также являются высотами и медианами. Пусть \(H\) – точка касания окружности со стороной \(AB\) (то есть \(OH\) – радиус). Следовательно, \(OH\perp AB\) (как часть высоты) и \(OH=\frac13CH\) (как часть медианы, так как медианы точкой пересечения делятся в отношении \(2:1\), считая от вершины).

Если \(AC=2x\), то \(AH=x\), следовательно, \(CH=\sqrt{4x^2-x^2}=x\sqrt3\), тогда \[\dfrac{\sqrt3}6=OH=\dfrac13\cdot CH=\dfrac{\sqrt3}3x\quad\Rightarrow\quad
x=\dfrac12\quad\Rightarrow\quad AC=2x=1\]
2 способ.
Площадь правильного треугольника со стороной \(a\) равна \(S=\dfrac{\sqrt3}4a^2\). Тогда по формуле \(S=p\cdot r\), где \(p\) – полупериметр, \(r\) – радиус вписанной окружности, имеем: \[\dfrac{\sqrt3}4a^2=\dfrac{3a}2\cdot r\quad\Rightarrow\quad a=2\sqrt3r=1\]
На этапе подготовки к ЕГЭ старшеклассники повторяют базовые определения и формулы, в том числе и по теме «Окружность, вписанная в многоугольник или угол». Достаточно подробное изучение данного раздела планиметрии осуществляется, как правило, в средней школе. В связи с этим необходимость повторения основных формул и понятий по теме «Окружность, вписанная в угол или многоугольник» на этапе подготовки к ЕГЭ возникает у многих выпускников. Поняв принцип решения подобных заданий, старшеклассники смогут рассчитывать на получение достаточно высоких баллов по итогам сдачи единого государственного экзамена.
Готовьтесь к ЕГЭ вместе с образовательным порталом «Школково»
Занимаясь перед прохождением аттестационного испытания, многие старшеклассники сталкиваются с проблемой поиска базовых понятий и формул для нахождения радиуса окружности, вписанной в правильный многоугольник, и других параметров. Далеко не всегда их легко найти в Интернете, как и, например, задачи на правильный шестиугольник. А школьного учебника может просто не оказаться под рукой в нужное время. Для того чтобы ликвидировать пробелы в знаниях по этому и другим математическим разделам, обратитесь к образовательному проекту «Школково». На нашем сайте представлен весь необходимый материал, изложенный доступно и понятно. Какими свойствами обладает окружность, вписанная в угол и многоугольник, и какие формулы необходимо знать для успешного решения задач по данной теме? Ответы на эти и другие вопросы вы найдете на сайте «Школково» в разделе «Теоретическая справка».
Чтобы подготовка к единому госэкзамену была действительно эффективной, рекомендуем также попрактиковаться в решении соответствующих задач. Большая база заданий представлена в разделе «Каталог». Для каждого упражнения наши специалисты прописали подробный ход решения и указали правильный ответ. Перечень задач на сайте постоянно дополняется и обновляется.



