Окружность, вписанная в многоугольник или угол (страница 2)

Окружность называется вписанной в выпуклый многоугольник/угол, если она касается всех сторон этого многоугольника/угла.
Тогда многоугольник/угол называется описанным около окружности.
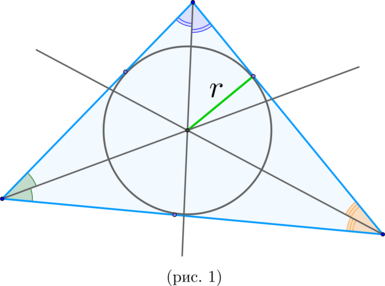
\(\blacktriangleright\) В любой треугольник можно вписать окружность. Ее центр лежит на пересечении биссектрис треугольника (рис. 1).
Площадь описанного треугольника ищется по формуле \[{\Large{S_{\triangle}=p\cdot r}},\]
где \(p\) – полупериметр.
\(\blacktriangleright\) Если в прямоугольный треугольник вписана окружность, \(a, b\) – катеты, \(c\) – гипотенуза, \(r\) – радиус этой окружности, то верна формула: \[{\large{r=\dfrac{a+b-c}2}}\] 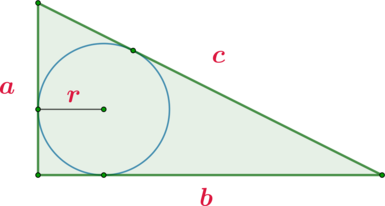
\(\blacktriangleright\) Если в выпуклый четырехугольник можно вписать окружность, то суммы его противоположных сторон равны.
И наоборот: если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность (рис. 2).
Центр вписанной окружности лежит на пересечении биссектрис углов.
Площадь описанного четырехугольника ищется по формуле
\[{\large{S_{\text{опис.4-к}}=p\cdot r}},\]
где \(p\) – полупериметр.

\(\blacktriangleright\) Если в параллелограмм вписана окружность, то он – ромб (рис. 3).
\(\blacktriangleright\) Если в прямоугольник вписана окружность, то он – квадрат (рис. 4).
\(\blacktriangleright\) Если в угол вписана окружность, то ее центр лежит на биссектрисе этого угла (рис. 5).

Сторона ромба равна \(1\), острый угол равен \(30^\circ\). Найдите радиус окружности, вписанной в этот ромб.

Для любого многоугольника, в который можно вписать окружность, верно \(S=p\cdot r\), где \(p\) – полупериметр, а \(r\) – радиус вписанной окружности.
\(S_{\text{ромб}}=S=a^2\cdot \sin\alpha\), где \(a\) – сторона ромба, \(\alpha\) – его угол. Следовательно, \(S=1^2\cdot \frac12=\frac12\). Полупериметр ромба равен \(2\). Тогда \[r=\dfrac Sp=0,25\]
Острый угол ромба равен \(30^\circ\), радиус вписанной в этот ромб окружности равен \(2\). Найдите сторону ромба.

Для любого многоугольника, в который можно вписать окружность, верно \(S=p\cdot r\), где \(p\) – полупериметр, а \(r\) – радиус вписанной окружности.
\(S_{\text{ромб}}=S=a^2\cdot \sin\alpha\), где \(a\) – сторона ромба, \(\alpha\) – его угол. Следовательно, \(S=a^2\cdot
\frac12=\frac12a^2\). Полупериметр ромба равен \(2a\). Тогда \[\dfrac12a^2=2a\cdot 2\quad\Rightarrow\quad a=8\]
Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен \(\sqrt3\).
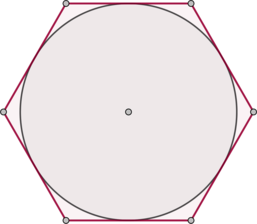
Для любого многоугольника, в который можно вписать окружность, верно \(S=p\cdot r\), где \(p\) – полупериметр, а \(r\) – радиус вписанной окружности.
Площадь правильного шестиугольника со стороной \(a\) равна \(S=\dfrac{3\sqrt3}2a^2\), полупериметр равен \(3a\), тогда \[\dfrac{3\sqrt3}2a^2=3a\cdot \sqrt3\quad\Rightarrow\quad a=2\]
Боковые стороны трапеции, описанной около окружности, равны \(9\) и \(12\). Найдите среднюю линию трапеции.
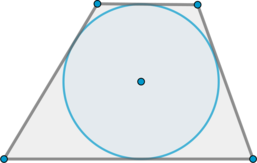
Если в четырехугольник можно вписать окружность, то суммы его противоположных сторон равны. Следовательно, сумма оснований трапеции равна сумме боковых сторон, то есть равна \(9+12=21\). Так как средняя линия трапеции равна полусумме оснований, то ответ: \(21:2=10,5\).
В треугольнике \(ABC\) \(AC=4, BC=3\), угол \(C\) равен \(90^\circ\). Найдите радиус вписанной окружности.
Известно, что для любого треугольника \(S_{\triangle}=p\cdot r\), где \(p\) – полупериметр, \(r\) – радиус вписанной окружности.
В нашем случае \(S_{\triangle}=0,5\cdot 3\cdot 4=6\). Гипотенуза по теореме Пифагора равна \(\sqrt{3^2+4^2}=5\), следовательно, \[r=\dfrac Sp=\dfrac{6}{0,5(3+4+5)}
= 1\]
Катеты равнобедренного прямоугольного треугольника равны \(2+\sqrt2\). Найдите радиус окружности, вписанной в этот треугольник.
Известно, что для любого треугольника \(S_{\triangle}=p\cdot r\), где \(p\) – полупериметр, \(r\) – радиус вписанной окружности.
В нашем случае \(S_{\triangle}=0,5\cdot (2+\sqrt2)(2+\sqrt2)\). Гипотенуза по теореме Пифагора равна \(\sqrt2(2+\sqrt2)\), следовательно, \[r=\dfrac Sp=\dfrac{0,5 (2+\sqrt2)^2}{0,5 (2+\sqrt2+2+\sqrt2+\sqrt2(2+\sqrt2))}
= 1\]
Периметр треугольника равен \(12\), а радиус вписанной окружности равен \(1\). Найдите площадь этого треугольника.
Так как \(S_{\triangle}=p\cdot r\), где \(p\) – полупериметр, \(r\) – радиус вписанной окружности, то \[S_{\triangle}=\dfrac{12}2\cdot 1=6\]



