Окружность, вписанная в многоугольник или угол (страница 3)

Окружность называется вписанной в выпуклый многоугольник/угол, если она касается всех сторон этого многоугольника/угла.
Тогда многоугольник/угол называется описанным около окружности.
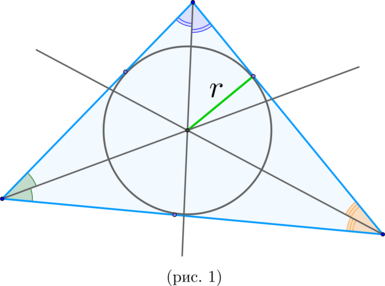
\(\blacktriangleright\) В любой треугольник можно вписать окружность. Ее центр лежит на пересечении биссектрис треугольника (рис. 1).
Площадь описанного треугольника ищется по формуле \[{\Large{S_{\triangle}=p\cdot r}},\]
где \(p\) – полупериметр.
\(\blacktriangleright\) Если в прямоугольный треугольник вписана окружность, \(a, b\) – катеты, \(c\) – гипотенуза, \(r\) – радиус этой окружности, то верна формула: \[{\large{r=\dfrac{a+b-c}2}}\] 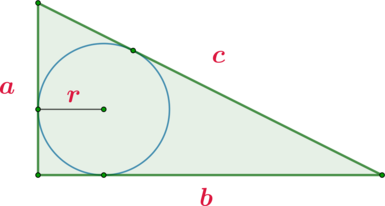
\(\blacktriangleright\) Если в выпуклый четырехугольник можно вписать окружность, то суммы его противоположных сторон равны.
И наоборот: если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность (рис. 2).
Центр вписанной окружности лежит на пересечении биссектрис углов.
Площадь описанного четырехугольника ищется по формуле
\[{\large{S_{\text{опис.4-к}}=p\cdot r}},\]
где \(p\) – полупериметр.

\(\blacktriangleright\) Если в параллелограмм вписана окружность, то он – ромб (рис. 3).
\(\blacktriangleright\) Если в прямоугольник вписана окружность, то он – квадрат (рис. 4).
\(\blacktriangleright\) Если в угол вписана окружность, то ее центр лежит на биссектрисе этого угла (рис. 5).

К окружности, вписанной в треугольник \(ABC\), проведены три касательные, параллельные сторонам треугольника. Периметры отсеченных треугольников равны \(5, 6\) и \(7\). Найдите периметр треугольника \(ABC\).
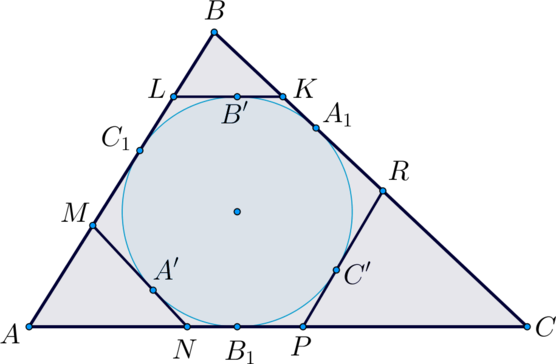
Рассмотрим рисунок. Пусть \(A_1, B_1, C_1\) – точки касания сторон \(\triangle ABC\) с окружностью. \(A', B', C'\) – точки на окружности, через которые проведены касательные параллельно сторонам треугольника. Получились треугольники \(AMN, BLK, CPR\). Пусть \(P_{AMN}=5, P_{BLK}=6, P_{CPR}=7\).
Так как отрезки касательных, проведенных из одной точки к окружности, равны, то \(MA'=MC_1, NA'=NB_1\). Следовательно, \[P_{AMN}=AM+MA'+NA'+AN=AM+MC_1+NB_1+AN=AC_1+AB_1=5\] Аналогично для других треугольников: \[\begin{aligned}
&P_{BLK}=BC_1+BA_1=6\\
&P_{CPR}=CA_1+CB_1=7 \end{aligned}\] Следовательно, \[P_{ABC}=(AC_1+AB_1)+(BC_1+BA_1)+(CA_1+CB_1)=5+6+7=18.\]
В треугольник \(ABC\) вписана окружность с центром в точке \(O\), причем \(\angle BAO=20^\circ\), \(\angle OBA=35^\circ\). Найдите \(\angle BCO\). Ответ дайте в градусах.
Т.к. центр вписанной окружности лежит на пересечении биссектрис углов треугольника, то \(AO, BO, CO\) – биссектрисы углов \(A, B, C\) соответственно.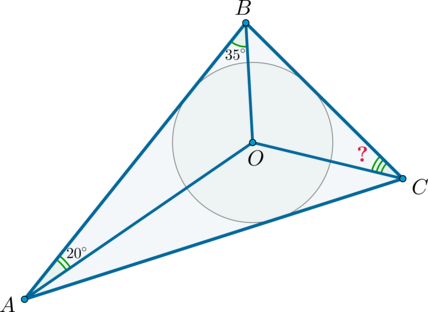
Следовательно, \(\angle A+\angle B+\angle C=2\angle BAO+2\angle
ABO+2\angle BCO=180^\circ\), откуда \(\angle BCO=90^\circ -\angle
BAO-\angle ABO=90^\circ-20^\circ-35^\circ=35^\circ\).
Окружность \(S\) касается стороны \(BC\) и продолжений сторон \(AB\) и \(AC\) треугольника \(ABC\). Найдите длину отрезка касательной к окружности \(S\), проведенной из точки \(A\), если периметр треугольника \(ABC\) равен \(20\).
Рассмотрим рисунок: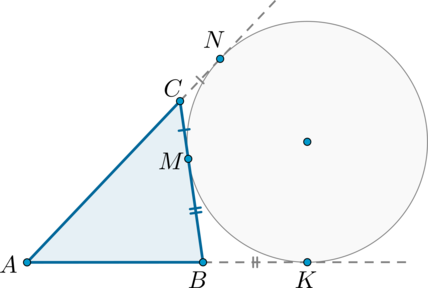
Т.к. отрезки касательных, проведенных из одной точки, равны, то \(CN=CM\), \(BM=BK\), \(AN=AK\). Таким образом, периметр
\(P=AC+CB+BA=AC+CM+MB+BA=AC+CN+BK+BA=\)
\(=(AC+CN)+(KB+BA)=AN+KA=2AN\)
Следовательно, \(AN=\frac12P=10\).
Около окружности, радиус которой равен \(4\), описан прямоугольный треугольник, гипотенуза которого равна \(20\). Найдите периметр этого треугольника.
Рассмотрим прямоугольный треугольник \(ABC\) (\(\angle C=90^\circ\)), \(AB=20\). Пусть \(O\) – центр вписанной в него окружности. Пусть также \(A_1, B_1, C_1\) – точки касания на сторонах \(BC, AC, AB\) соответственно.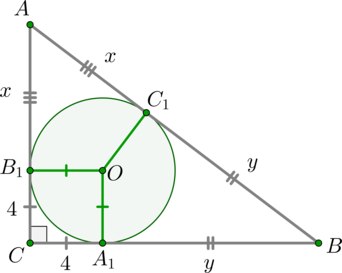
Т.к. отрезки касательных, проведенных из одной точки к окружности, равны, то \[AC_1=AB_1=x; \qquad BC_1=BA_1=y; \qquad CA_1=CB_1.\]
Заметим также, что радиусы \(OB_1\) и \(OA_1\) перпендикулярны \(AC\) и \(BC\) соответственно (как радиусы, проведенные в точку касания). Следовательно, \(CB_1OA_1\) – прямоугольник (четырехугольник, имеющий три прямых угла). Но т.к. его смежные стороны равны, то это – квадрат. Следовательно, \(CA_1=CB_1=4\).
Тогда периметр треугольника равен:
\[AB+BC+CA=(x+y)+(y+4)+(4+x)=2(x+y)+4+4=2\cdot 20+8=48.\]
В ромб со стороной \(8\) вписана окружность. Найдите радиус этой окружности, если площадь ромба равна \(10\).
Пусть дан ромб \(ABCD\), \(AB=8\), \(O\) – центр окружности, вписанной в этот ромб. Т.к. центр окружности, вписанной в многоугольник, лежит на пересечении биссектрис его углов, то \(O\) – точка пересечения диагоналей ромба (т.к. они являются биссектрисами углов ромба). Пусть \(K\) – точка касания окружности со стороной \(AB\). Тогда \(OK=r\) – радиус окружности.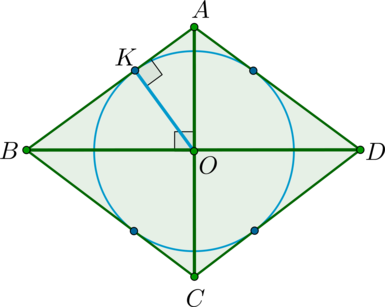
Рассмотрим треугольники \(OKA\) и \(OBA\). Они подобны по двум углам. Следовательно, \[\dfrac{OK}{OB}=\dfrac{OA}{AB} \quad \Rightarrow \quad r=OK=\dfrac{OA\cdot OB}{AB}\]
Т.к. площадь ромба равна полупроизведению диагоналей, то \(S=\frac12\cdot AC\cdot BD=\frac12\cdot 2\,OA\cdot 2\,OB=2\,OA\cdot OB=10\). Отсюда \(OA\cdot OB=5\). Следовательно,
\[r=\dfrac58=0,625.\]
В треугольник вписана окружность радиуса \(2,4\sqrt3\). Одна из сторон треугольника равна \(13\), а разность двух других равна \(5\). Найдите большую сторону этого треугольника.
1) Пусть в треугольнике \(BC=13\), \(AC-AB=5\). Таким образом, наибольшей стороной будет или \(AC\), или \(BC\).
Т.к. отрезки касательных, проведенных из одной точки к окружности, равны, то \(AM=AK=a\), \(BM=BN=b\), \(CN=CK=c\) (где \(M,N,K\) – точки касания).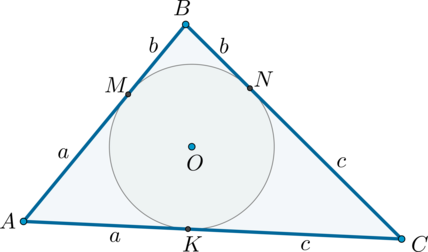
Таким образом, из условия следует, что \(b+c=13\), \(a+c-(a+b)=c-b=5\). Решая систему из этих двух уравнений, находим, что \(b=4\), \(c=9\).
2) Заметим, что полупериметр данного треугольника равен \(a+b+c=a+13\), а площадь по формуле Герона равна
\(S=\sqrt{(a+b+c)(a+b+c-(a+b))(a+b+c-(a+c))(a+b+c-(b+c))}=\)
\(=\sqrt{(a+b+c)\cdot a\cdot b\cdot c}=6\sqrt{a(a+13)}.\)
Тогда по формуле (площадь равна полупериметру, умноженному на радиус вписанной окружности) имеем:
\[S=(a+b+c)\cdot r \quad \Rightarrow \quad 6\sqrt{a(a+13)}= (a+13)\cdot 2,4\sqrt3 \quad \Rightarrow \quad 36a=(a+13)\cdot \left(\dfrac{12}5\sqrt3\right)^2,\]
откуда \(a=12\). Следовательно, \(AC=12+9=21>BC\). Значит, большая сторона равна \(21\).
Окружность вписана в угол \(B\), равный \(60^\circ\). Найдите радиус этой окружности, если расстояние между точками касания окружности и сторон угла равно \(3\sqrt3\).
Обозначим точки касания окружности и сторон угла за \(A\) и \(C\). Тогда известно, что \(AC=3\sqrt3\). Пусть также \(O\) – центр окружности.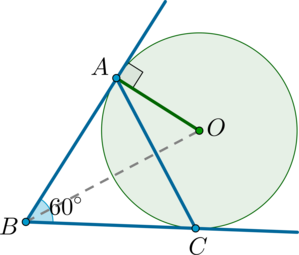
Тогда \(OA\) – радиус окружности, причем \(OA\perp BA\) (т.к. \(BA\) – касательная, а радиус, проведенный в точку касания, перпендикулярен касательной).
Рассмотрим \(\triangle ABC\): он равнобедренный (\(AB=BC\) как отрезки касательных, проведенных из одной точки), следовательно, \(\angle A=\angle C=0,5\cdot(180^\circ-60^\circ)=60^\circ\). Таким образом, он равносторонний, следовательно, \(AB=AC=3\sqrt3\).
Т.к. окружность вписана в угол, то ее центр лежит на биссектрисе этого угла, то есть \(\angle ABO=30^\circ\). Тогда из прямоугольного \(\triangle ABO\):
\[\mathrm{tg}\,30^\circ=\dfrac{OA}{BA}=\dfrac{OA}{3\sqrt3} \quad \Rightarrow \quad OA=3\sqrt3\cdot \dfrac{\sqrt3}3=3.\]



