Правильный шестиугольник (страница 2)

Правильный шестиугольник - выпуклый шестиугольник, у которого все углы равны и все стороны равны.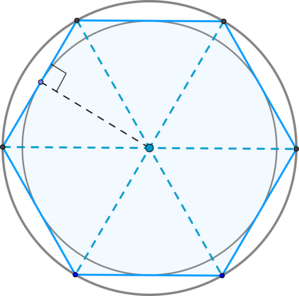
\(\blacktriangleright\) Каждый угол правильного шестиугольника равен \(120^\circ\).
\(\blacktriangleright\) Около правильного шестиугольника можно описать окружность: ее радиус равен его стороне.
\(\blacktriangleright\) Большие диагонали правильного шестиугольника делят его на \(6\) равносторонних треугольников, у которых высота равна радиусу вписанной в правильный шестиугольник окружности.
\(\blacktriangleright\) Центры вписанной и описанной около правильного шестиугольника окружностей есть точка пересечения больших диагоналей этого шестиугольника.
\(\blacktriangleright\) Площадь правильного шестиугольника со стороной \(a\) равна \[S=\dfrac{3\sqrt3}2a^2\]
Сторона правильного шестиугольника \(ABCDEF\) равна \(\sqrt[4]{3}\). Найдите его площадь.
Пусть \(O\) – центр описанной около \(ABCDEF\) окружности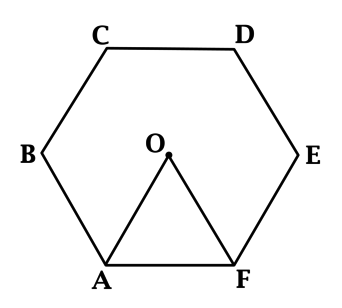
тогда треугольники \(AOF\), \(AOB\), \(BOC\), \(COD\), \(DOE\), \(EOF\) – равносторонние и все они попарно равны.
\[S_{\triangle{AOF}} = 0,5 AF^2 \cdot \sin{60^{\circ}} = \dfrac{AF^2\sqrt{3}}{4}, \qquad\qquad S_{ABCDEF} = 6\cdot S_{\triangle{AOF}} = \dfrac{3\sqrt{3}AF^2}{2}.\] В данной задаче \(S_{ABCDEF} = 6\cdot S_{\triangle{AOF}} = \dfrac{3\sqrt{3}AF^2}{2} = 4,5\).
Найдите расстояние между двумя параллельными сторонами правильного шестиугольника со стороной \(\sqrt{108}\).
Рассмотрим правильный шестиугольник \(ABCDFE\) и в нем треугольник \(ABC\). Параллельными сторонами являются пары \(AB\) и \(DF\), \(BC\) и \(FE\), \(CD\) и \(EA\).
Помним, что угол правильного шестиугольника равен \(120^\circ\).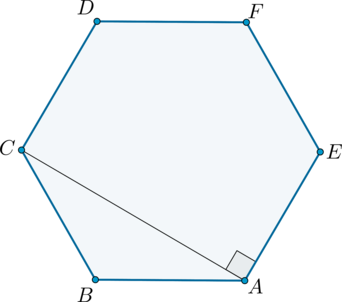
\(\triangle ABC\) равнобедренный (\(AB=BC\,\)), следовательно, \(\angle BAC=0,5\cdot (180^\circ-120^\circ)=30^\circ\). Таким образом, \(\angle CAE=120^\circ-30^\circ=90^\circ\).
Следовательно, \(AC\) – расстояние между сторонами \(AE\) и \(CD\) (по определению расстояние между двумя параллельными прямыми – отрезок, проведенный из любой точки одной прямой перпендикулярно ко второй прямой).
Найдем \(AC\) по теореме косинусов (\(AB=BC=a=\sqrt{108}\)):
\(AC^2=a^2+a^2-2a^2\cdot \cos120^\circ=2a^2(1-\cos120^\circ)=2\cdot 108\cdot \left(1+\frac12\right)=3\cdot 108 \quad \Rightarrow \)
\(\Rightarrow \quad AC=\sqrt{3\cdot 108}=\sqrt{3\cdot 3\cdot 36}=3\cdot 6=18.\)
Около правильного шестиугольника \(ABCDEF\) описана окружность с центром в точке \(O\). Во сколько раз площадь этого шестиугольника больше площади треугольника \(AOK\), где \(K\) – середина стороны \(BC\).
По свойству правильного шестиугольника центр описанной окружности лежит на пересечении больших его диагоналей. Следовательно, \(AO\) – радиус описанной окружности. Также по свойству радиус описанной окружности равен стороне правильного шестиугольника, следовательно, \(AB=AO=x\).
Т.к. \(\triangle AOB\) – правильный, то \(\angle AOB=60^\circ\). \(\triangle BOC\) также правильный. Т.к. по условию \(OK\) – медиана в правильном \(\triangle BOC\), то она и биссектриса, то есть \(\angle
BOK=\frac12\cdot 60^\circ=30^\circ\). Таким образом, \(\angle
AOK=90^\circ\), то есть \(\triangle AOK\) – прямоугольный.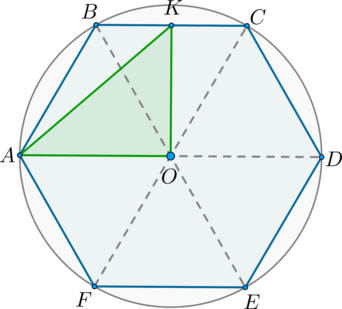
Следовательно, \[S_{\triangle AOK}=\dfrac12\cdot AO\cdot OK=\dfrac x2\cdot OK\]
Площадь правильного шестиугольника равна сумме площадей шести правильных треугольников:
\[S_{ABCDEF}=6\cdot \dfrac12\cdot BC\cdot OK=6\cdot \dfrac x2\cdot OK\]
Таким образом, \[\dfrac{S_{ABCDEF}}{S_{\triangle AOK}}=6.\]
Около правильного шестиугольника \(ABCDEF\) описана окружность с центром в точке \(O\). Найдите большую сторону треугольника \(AOK\), где \(K\) – середина стороны \(BC=\sqrt7\) шестиугольника \(ABCDEF\).
По свойству правильного шестиугольника центр описанной окружности лежит на пересечении больших его диагоналей. Следовательно, \(AO\) – радиус описанной окружности. Также по свойству радиус описанной окружности равен стороне правильного шестиугольника, следовательно, \(AB=AO=\sqrt7\).
Т.к. \(\triangle AOB\) – правильный, то \(\angle AOB=60^\circ\). \(\triangle BOC\) также правильный. Т.к. по условию \(OK\) – медиана в правильном \(\triangle BOC\), то она и биссектриса, то есть \(\angle
BOK=\frac12\cdot 60^\circ=30^\circ\). Таким образом, \(\angle
AOK=90^\circ\), то есть \(\triangle AOK\) – прямоугольный.
Следовательно, большая сторона в \(\triangle AOK\) – это гипотенуза \(AK\). По теореме Пифагора из \(\triangle BOK\) (\(OK\) также является в нем высотой):
\[OK=\sqrt{BO^2-BK^2}=\sqrt{(\sqrt7)^2-\left(\dfrac{\sqrt7}2\right)^2}= \dfrac{\sqrt3}2\cdot \sqrt7\]
Таким образом, по теореме Пифагора из \(\triangle AOK\):
\[AK=\sqrt{AO^2+OK^2}=\sqrt{(\sqrt7)^2+\left(\dfrac{\sqrt3}2\cdot \sqrt7\right)^2}= \dfrac72=3,5.\]


