Теорема синусов и теорема косинусов (страница 2)

\(\blacktriangleright\) Теорема синусов: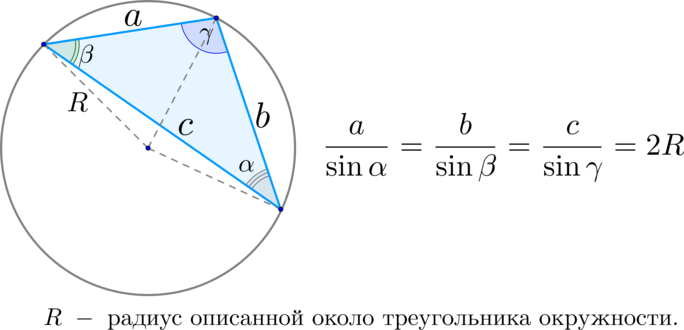
\(\blacktriangleright\) Теорема косинусов: \(\Large{a^2=b^2+c^2-2bc\cdot \cos \angle(b,c)}\)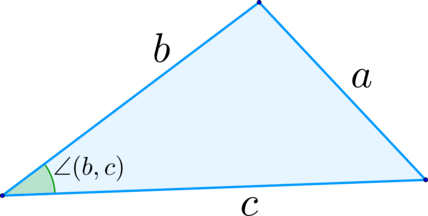
В треугольнике \(ABC\) проведена медиана \(AM\). Найдите площадь треугольника \(ABC\), если \(AC = 3\sqrt{2}, BC = 10, \angle MAC = 45^\circ\).
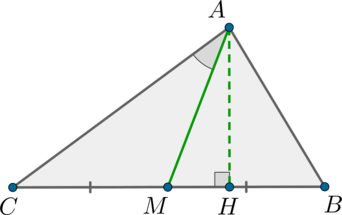
Из треугольника \(ACM\) по теореме косинусов найдем \(AM\):
\[CM^2 = AC^2 + AM^2 - 2\cdot AC\cdot AM\cdot \cos{45^\circ}\Rightarrow AM = 7.\]
Т.к. \(AM\) - медиана \(\Rightarrow\) она делит треугольник \(ABC\) на два равновеликих треугольника:
\[S_{ABC} = 2\cdot S_{ACM} = 2\cdot 0,5\cdot AC\cdot AM\cdot \sin{45^\circ} = 21.\]
Площадь треугольника \(ABC\) равна \(20\sqrt{3}\). Найдите \(AC\), если сторона \(AB\) равна 8, а медиана \(BM\) равна 5.
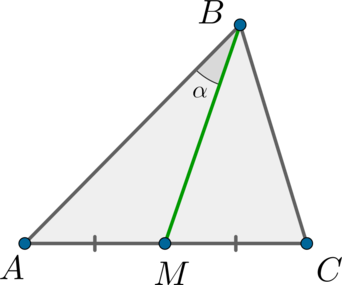
Т.к. \(BM\) - медиана \(\Rightarrow\) она делит треугольник \(ABC\) на два равновеликих треугольника:
\[S_{ABM} = S_{BMC} = 10\sqrt{3} = 0,5\cdot AB\cdot BM\cdot \sin{\alpha}.\]
\[\sin{\alpha} = \dfrac{\sqrt{3}}2\Rightarrow \alpha = 60^\circ.\]
Воспользуемся теоремой косинусов и найдем \(AM\):
\[AM = \sqrt{AB^2 + BM^2 - 2\cdot AB\cdot BM\cdot \cos{\alpha}} = 7 \Rightarrow AC = 14.\]
Найдите площадь треугольника \(KPM\), если сторона \(KP = 5\), медиана \(PO = 3\sqrt{2}, \angle KOP = 135^\circ\)
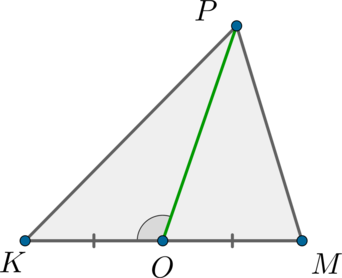
Из треугольника \(KPO\) найдем \(KO\) по теореме Косинусов:
\[PK^2 = KO^2 + OP^2 - 2\cdot KO\cdot OP\cdot \cos{135^\circ}\Rightarrow KO = 1.\]
Т.к. \(PO\)- медиана \(\Rightarrow\) она делит треугольник \(KPM\) на два равновеликих треугольника:
\[S_{KPM} = 2\cdot S_{KPO} = 2\cdot 0,5\cdot KO\cdot OP\cdot \sin{135^\circ} = 3.\]
В треугольнике \(ABC\): \(\ O\) – точка пересечения серединных перпендикуляров к сторонам \(AB\) и \(AC = 5\sqrt{3}\), \(OD\) – серединный перпендикуляр к стороне \(CA\), \(\angle B = 60^{\circ}\). Найдите \(OD\).
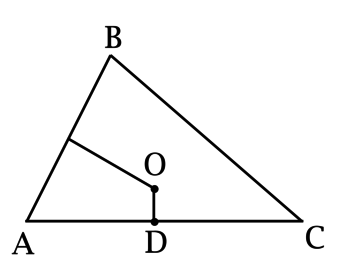
Так как \(O\) – точка пересечения серединных перпендикуляров в треугольнике \(ABC\), то \(O\) – центр описанной около \(ABC\) окружности, \(AO = R\).
По теореме Пифагора: \[R^2 = AD^2 + OD^2.\] По теореме синусов \[2R = \dfrac{AC}{\sin\angle B} = \dfrac{5\sqrt{3}}{\frac{\sqrt{3}}{2}} = 10\qquad\Rightarrow\qquad R = 5\qquad\Rightarrow\qquad 25 = \dfrac{25\cdot 3}4 + OD^2,\] следовательно, \(OD^2 = \frac{25}4\). Так как \(OD > 0\), то \(OD = \frac52=2,5\).
В треугольнике \(ABC\): \(\angle C = 60^{\circ}\), \(AC = 8\), \(AB = 7\). Найдите \(BC\), если известно, что \(BC > 4\).
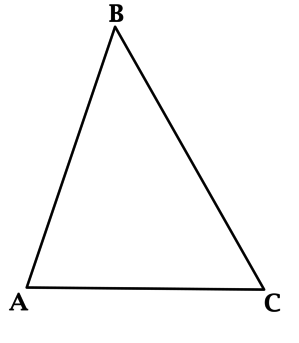
По теореме косинусов \(AB^2 = AC^2 + BC^2 - 2\cdot AC\cdot BC\cdot \cos{\angle ACB}\).
Обозначим \(BC\) за \(x\), тогда \(49 = 64 + x^2 - 8x\), откуда получаем \[x^2 - 8x + 15 = 0.\] Корни этого уравнения \(x_1 = 3\), \(x_2 = 5\).
Так как \(BC > 4\), то подходит только \(x = 5\). Итого: \(BC = 5\).
В треугольнике \(ABC\): \(\angle A = 45^{\circ}\), \(O\) – точка пересечения серединных перпендикуляров к сторонам \(AB\) и \(BC\), \(OD = 44\) – серединный перпендикуляр к стороне \(CB\). Найдите \(CB\).
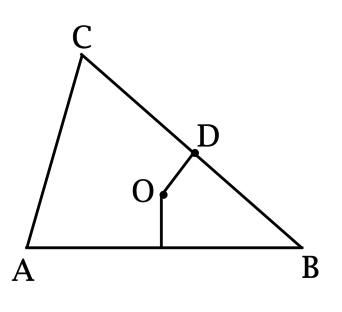
Так как \(O\) – точка пересечения серединных перпендикуляров в треугольнике \(ABC\), то \(O\) – центр описанной около \(ABC\) окружности, \(OC = R\).
Обозначим \(BC = a\). По теореме Пифагора \[R^2 = \left(\dfrac{a}{2}\right)^2 + OD^2.\] По теореме синусов \[\dfrac{a}{\sin\angle A} = 2R,\] тогда \[\dfrac{a}{\frac{\sqrt{2}}{2}} = 2R\qquad\Rightarrow\qquad R = \dfrac{a}{\sqrt{2}}.\]
\(\dfrac{a^2}{2} = \dfrac{a^2}{4} + OD^2\), тогда \(a^2 = 4\cdot OD^2\), откуда \(a = \pm 2\cdot OD\), но \(a > 0\), \(OD > 0\), следовательно, \(a = 2\cdot OD = 88\).
В треугольнике \(ABC\): \(\angle B = 30^{\circ}\), \(O\) – точка пересечения серединных перпендикуляров к сторонам \(AC\) и \(BC\), \(OD\) – серединный перпендикуляр к стороне \(AC\). Найдите \(\dfrac{\sqrt{3}\cdot AC}{OD}\).
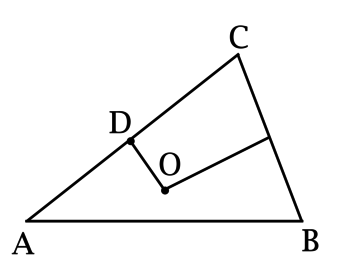
Так как \(O\) – точка пересечения серединных перпендикуляров в треугольнике \(ABC\), то \(O\) – центр описанной около \(ABC\) окружности, \(OC = R\).
Обозначим \(AC = a\), \(OD = h\). По теореме Пифагора \[R^2 = \left(\dfrac{a}{2}\right)^2 + h^2.\] По теореме синусов \[\dfrac{a}{\sin\angle B} = 2R\qquad\Rightarrow\qquad \dfrac{a}{\frac{1}{2}} = 2R\qquad\Rightarrow\qquad R = a.\]
\(a^2 = \dfrac{a^2}{4} + h^2\), тогда \(\dfrac{a^2}{h^2} = \dfrac{4}{3}\), откуда \(\dfrac{a}{h} = \pm\dfrac{2}{\sqrt{3}}\), но \(a > 0\), \(h > 0\), следовательно, \(\dfrac{a}{h} = \dfrac{2}{\sqrt{3}}\), тогда \(\dfrac{a\sqrt{3}}{h} = 2\).



