Теорема синусов и теорема косинусов (страница 3)

\(\blacktriangleright\) Теорема синусов: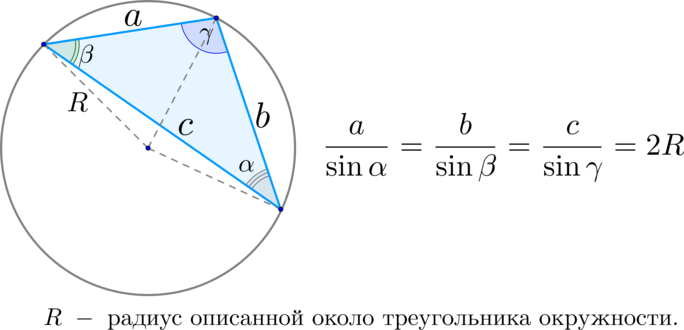
\(\blacktriangleright\) Теорема косинусов: \(\Large{a^2=b^2+c^2-2bc\cdot \cos \angle(b,c)}\)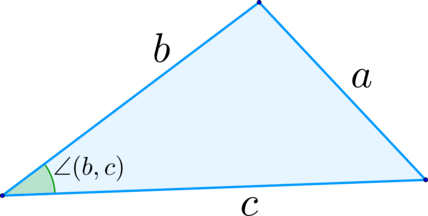
В треугольнике \(ABC\): \(\ O\) – точка пересечения серединных перпендикуляров к сторонам \(AC\) и \(BC = 5\pi < AB\), \(OD = 2,5\pi\) – серединный перпендикуляр к стороне \(CB\). Найдите \(\angle A\). Ответ дайте в градусах.
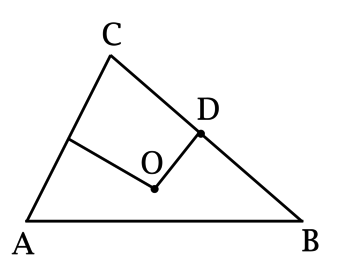
Так как \(O\) – точка пересечения серединных перпендикуляров в треугольнике \(ABC\), то \(O\) – центр описанной около \(ABC\) окружности, \(OC = R\).
По теореме Пифагора \[R^2 = CD^2 + OD^2 = 2\cdot 2,5^2\cdot\pi^2\qquad\Rightarrow\qquad R = 2,5\sqrt{2}\pi\] По теореме синусов \[\dfrac{BC}{\sin\angle A} = 2R \qquad\Rightarrow\qquad \dfrac{5\pi}{\sin\angle A} = 5\sqrt{2}\pi \qquad\Rightarrow\qquad \sin\angle A = \dfrac{1}{\sqrt{2}},\] следовательно, \(\angle A = 45^{\circ}\) или \(\angle A = 135^{\circ}\), но \(AB > BC\), а в треугольнике против большего угла лежит большая сторона, тогда \(\angle A = 45^{\circ}\).
В треугольнике \(ABC\): \(\ O\) – точка пересечения серединных перпендикуляров к сторонам \(AC\) и \(BC\), \(OD\) – серединный перпендикуляр к стороне \(CA\), \(\dfrac{AC}{OD} = 2\sqrt{3}\). Найдите \(\sqrt{3}\cdot\sin\angle B\).
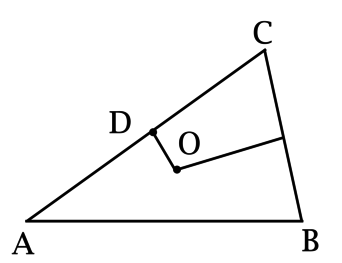
Так как \(O\) – точка пересечения серединных перпендикуляров в треугольнике \(ABC\), то \(O\) – центр описанной около \(ABC\) окружности, \(OC = R\).
Обозначим \(OD = h\), тогда \(AC = 2h\sqrt{3}\).
По теореме Пифагора \[R^2 = CD^2 + OD^2 = 4h^2\qquad\Rightarrow\qquad R = 2h.\] По теореме синусов \[\dfrac{AC}{\sin\angle B} = 2R\qquad\Rightarrow\qquad \dfrac{2h\sqrt{3}}{\sin\angle B} = 4\cdot h,\] откуда \(\sin\angle B = \dfrac{\sqrt{3}}{2}\), следовательно, \(\sqrt{3}\cdot\sin\angle B = 1,5\).
В треугольнике \(ABC\): \(BD\) – медиана, \(\angle ABC\) – острый, \(BC = 3\), \(\sin{\angle A} = \dfrac{3\sqrt{3}}{8}\), \(AC = 4\), \(BD = \dfrac{3\sqrt{3}}{2\sqrt{2}}\). Найдите \(\angle DBC\). Ответ дайте в градусах.
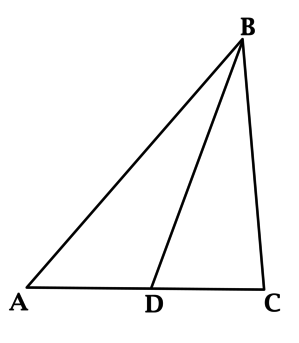
По теореме синусов в треугольнике \(ABC\) \[\dfrac{AB}{\sin{\angle C}} = \dfrac{BC}{\sin{\angle A}} = \dfrac{CA}{\sin{\angle B}} = 2R,\] где \(R\) – радиус описанной около \(ABC\) окружности.
Тогда \[\dfrac{CA}{\sin{\angle ABC}} = \dfrac{BC}{\sin{\angle A}}\] и, значит, \[\dfrac{4}{\sin{\angle ABC}} = \dfrac{8}{\sqrt{3}} \qquad\Rightarrow\qquad \sin{\angle ABC} = \dfrac{\sqrt{3}}{2}.\] \(\sin{\angle ABC} = \dfrac{\sqrt{3}}{2}\) и \(\angle ABC\) – острый, тогда \(\angle ABC = 60^{\circ}\).
По теореме синусов в треугольнике \(ABD\) \[\dfrac{AD}{\sin{\angle ABD}} = \dfrac{BD}{\sin{\angle BAD}},\] тогда \[\dfrac{2}{\sin{\angle ABD}} = \dfrac{4}{\sqrt{2}} \qquad\Rightarrow\qquad\sin{\angle ABD} = \dfrac{\sqrt{2}}{2}.\] \(\angle ABD\) – острый и \(\sin{\angle ABD} = \dfrac{\sqrt{2}}{2}\), тогда \(\angle ABD = 45^{\circ}\).
\(\angle DBC = \angle ABC - \angle ABD = 15^{\circ}\).
\(AB\) – диаметр окружности с центром \(O\), который пересекает хорду \(CD\) в точке \(E\), лежащей на \(BO\). Градусная мера дуги \(AC\) равна \(60^{\circ}\), \(OE = 0,6\cdot OA\). Найдите \(7\cdot \cos{\angle CEA}\).
Построим радиус \(CO\) и отрезок \(CA\), тогда \(\angle COA = 60^{\circ}\) и, следовательно, треугольник \(COA\) – равносторонний, \(\angle CAE = 60^{\circ}\), \(AC = AO\).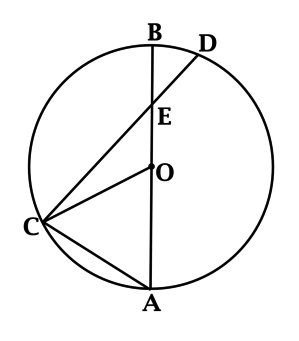
\(AE = 1,6\cdot AO\).
Запишем теорему косинусов для треугольника \(ACE\): \[CE^2 = AE^2 + AC^2 - 2\cdot AE\cdot AC\cdot \cos{\angle CAE},\] тогда \[CE^2 = 2,56\cdot AO^2 + AO^2 - 2\cdot 1,6\cdot AO\cdot AO\cdot 0,5 = 1,96\cdot AO^2,\] тогда \(CE = 1,4\cdot AO\).
По теореме синусов \[\dfrac{AC}{\sin{\angle AEC}} = \dfrac{CE}{\sin{\angle CAE}},\] тогда \[\dfrac{AO}{\sin{\angle AEC}} = \dfrac{1,4\cdot AO}{0,5\sqrt{3}}\qquad\Rightarrow\qquad \sin{\angle AEC} = \dfrac{\sqrt{3}}{2,8}.\]
Из основного тригонометрического тождества находим: \(\cos{\angle AEC} = \pm \dfrac{11}{14}\). Так как точка \(E\) лежит на \(BO\), то \(\angle AEC\) – острый, значит \[\cos{\angle AEC} = \dfrac{11}{14}\qquad\Rightarrow\qquad 7\cdot \cos{\angle AEC} = 5,5.\]
\(ABCD\) – вписанный четырёхугольник, причём \(\dfrac{AB}{CD} = 2 = \dfrac{AD}{BC}\), \(AC = 1\). Найдите \(BD\).
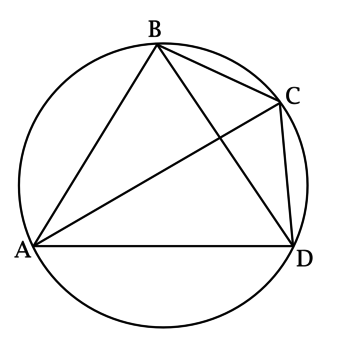
Обозначим \(BC = x\), \(CD = y\), \(\angle ABC = \alpha\), \(\angle BAD = \beta\).
Выразим \(AC^2\) при помощи теоремы косинусов в треугольниках \(ABC\) и \(ACD\):
\[AC^2 = x^2 + 4y^2 - 4xy\cos\alpha,\] так как \(\cos(\pi - \phi) = -\cos\phi\), то \[AC^2 = 4x^2 + y^2 + 4xy\cos\alpha.\] Складывая два последних равенства с учётом того, что \(AC = 1\), получим: \[2 = 5(x^2 + y^2)\qquad\Rightarrow\qquad x^2 + y^2 = 0,4.\] Выразим \(BD^2\) при помощи теоремы косинусов в треугольниках \(ABD\) и \(BCD\): \[BD^2 = 4x^2 + 4y^2 - 8xy\cos\beta,\qquad\qquad BD^2 = x^2 + y^2 + 2xy\cos\beta,\] откуда \[4x^2 + 4y^2 - 8xy\cos\beta = x^2 + y^2 + 2xy\cos\beta,\] но \(x^2 + y^2 = 0,4\), тогда \(xy\cos\beta = 0,12\).
В итоге \(BD^2 = x^2 + y^2 + 2xy\cos\beta = 0,4 + 2\cdot 0,12 = 0,64\), откуда \(BD = 0,8\).
\(ABCD\) – вписанный четырёхугольник, причём \(\dfrac{AB}{CD} = k = \dfrac{AD}{BC}\), \(AC = 5\), \(BD = 3\) Найдите \(k\), если \(AB > CD\).
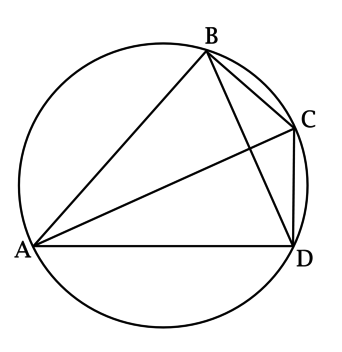
Обозначим \(BC = x\), \(CD = y\), \(\angle ABC = \alpha\), \(\angle BAD = \beta\).
Выразим \(AC^2\) при помощи теоремы косинусов в треугольниках \(ABC\) и \(ACD\):
\[AC^2 = x^2 + k^2y^2 - 2xky\cos\alpha,\] так как \(\cos(\pi - \phi) = -\cos\phi\), то \[AC^2 = k^2x^2 + y^2 + 2kxy\cos\alpha.\] Складывая два последних равенства с учётом того, что \(AC = 5\), получим: \[50 = (k^2 + 1)(x^2 + y^2)\qquad\Rightarrow\qquad x^2 + y^2 = \dfrac{50}{k^2 + 1}.\] Выразим \(BD^2\) при помощи теоремы косинусов в треугольниках \(ABD\) и \(BCD\):
\[BD^2 = k^2x^2 + k^2y^2 - 2kxky\cos\beta,\qquad\qquad BD^2 = x^2 + y^2 + 2xy\cos\beta,\] откуда \[k^2(x^2 + y^2) - 2k^2xy\cos\beta = x^2 + y^2 + 2xy\cos\beta,\] но \(x^2 + y^2 = \dfrac{50}{k^2 + 1}\), тогда \[\dfrac{(k^2 - 1)\cdot 50}{k^2 + 1} = 2(k^2 + 1)xy\cos\beta \qquad\Rightarrow\qquad xy\cos\beta = \dfrac{25(k^2 - 1)}{(k^2 + 1)^2}.\]
В итоге \[BD^2 = 9 = \dfrac{50}{k^2 + 1} + \dfrac{50(k^2 - 1)}{(k^2 + 1)^2} = \dfrac{50(k^2 + 1) + 50(k^2 - 1)}{(k^2 + 1)^2} = \dfrac{100k^2}{(k^2 + 1)^2} \qquad\Rightarrow\qquad 9(k^2 + 1)^2 = 100k^2.\]
Обозначим \(t = k^2\): \[9(t + 1)^2 = 100t\qquad\Leftrightarrow\qquad 9t^2 - 82t + 9 = 0.\] Дискриминант \(D = 6724 - 324 = 6400 = 80^2\). \[t_1 = \dfrac{82 + 80}{18} = 9, \ t_2 = \dfrac{82 - 80}{18} = \dfrac{1}{9}.\] Так как \(AB > CD\), то \(k > 1\), тогда \(t = k^2 > 1\), откуда \(t = 9\), следовательно, \(k = 3\) (\(k > 1\)).
В остроугольном треугольнике \(PQR\), сторона \(PR\) которого равна 12, на стороны \(QR\) и \(PQ\) опущены высоты \(PM\) и \(RN\). Вычислить площадь четырехугольника \(PNMR\), если известно, что площадь треугольника \(NQM\) равна 2, а радиус окружности, описанной около треугольника \(PQR\), равен \(\dfrac{9\sqrt{2}}2\).
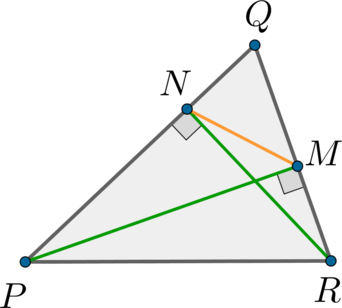
По теореме синусов:
\[\dfrac{PR}{\sin{\angle Q}} = 2R\Rightarrow \dfrac{12}{\sin{\angle Q}} = 2\cdot \dfrac{9\sqrt{2}}2 \Rightarrow \sin{\angle Q} = \dfrac{2\sqrt{2}}3.\]
\[\cos{\angle Q} = \sqrt{1 - (\sin{\angle Q})^2} = \dfrac{1}3.\]
\(\angle QNM = \angle QRP \Rightarrow\) треугольник \(PQR\) подобен треугольнику \(QMN\) по двум углам, тогда:
\[\dfrac{S_{QMN}}{S_{QPR}} = \left(\dfrac{QM}{QP}\right)^2 = (\cos{Q})^2 = \dfrac{1}9\Rightarrow S_{QPR} = 2\cdot 9 = 18.\]
\[S_{PNMR}= 18 - 2= 16.\]



