Смешанные неравенства —Каталог задач по ЕГЭ - Математика

Ошибка.
Попробуйте повторить позже

Задача 1#509

Решите неравенство

ln(5ex) ≥ 1

Показать ответ и решение

Так как $ex > 0$ – при любом $x$ , то

ln(5ex) ≥ 1 ⇔ ln (5ex ) ≥ ln e ⇔ 5ex ≥ e ⇔ eln5ex ≥ e ⇔ e ⇔ ex ≥ -ln5 ⇔ ex ≥ e1− ln5 ⇔ x ≥ 1 − ln5. e

Ответ:

$[1 − ln 5;+ ∞ )$

Ошибка.
Попробуйте повторить позже

Задача 2#510

Решите неравенство

x 1- ln(7e ) ≥ x

Показать ответ и решение

ОДЗ:

{ 7ex > 0 ⇔ x ⁄= 0. x ⁄= 0

На ОДЗ:

x 1- x 1x x 1x ln7 x 1x ln (7e ) ≥ x ⇔ ln(7e ) ≥ lne ⇔ 7e ≥ e ⇔ e e ≥ e ⇔ 1x 2 ⇔ ex ≥ -e-- ⇔ ex ≥ e 1x−ln7 ⇔ x ≥ 1-− ln7 ⇔ x--+-xln-7 −-1 ≥ 0. eln7 x x

По методу интервалов

$PIC$

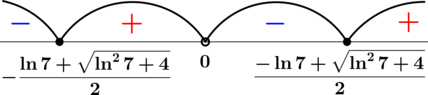
Таким образом, с учётом ОДЗ

[ ∘ -2------- ) [ ∘ --2------ ) x ∈ −-ln7-−----ln--7 +-4;0 ∪ −-ln7-+---ln--7 +-4;+ ∞ . 2 2

Ответ:

$[ ∘ --2------ ) [ ∘ --2------ ) −-ln-7 −---ln--7-+-4 −-ln-7 +---ln--7-+-4 2 ;0 ∪ 2 ;+ ∞$

Ошибка.
Попробуйте повторить позже

Задача 3#1815

Решите неравенство

ln (− 5ex) ≥ − 1

Показать ответ и решение

Так как $ex > 0$ – при любом $x$ , то $− 5ex < 0$ , следовательно, $ln (− 5ex)$ не определён ни при каких $x ∈ ℝ$ .

Ответ:

$∅$

Ошибка.
Попробуйте повторить позже

Задача 4#511

Решите неравенство

2 2 ln(x-+-1)⋅(logx24x-+-log24x−-log24)-≤0 (3 − 2)lnx

Показать ответ и решение

Найдем ОДЗ:

( 2 ||| x + 1> 0 ( ||||{ 4x> 0 ||{ x⁄= log3 2 3x− 2⁄= 0 ⇔ x> 0 |||| ||( |||( x> 0 x⁄= 1 x⁄= 1

На ОДЗ $2 x + 1> 1,$ следовательно, $2 ln(x +1) >0.$ Тогда исходное неравенство на ОДЗ равносильно

log224x+-log2-4x-−-log24-≤0 (3x − 2)lnx

Найдём нули числителя:

log224x+ log24x − log24= 0

Сделаем замену $log24x= t:$

t2+ t− 2= 0 ⇔ t= −1-±3- 2

Сделаем обратную замену:

log 4x= − 2 ⇔ log 4x =log 0,25 2 2 1 2 4x= 0,25 ⇔ x = 16 log24x= 1 ⇔ log24x= log22 4x= 2 ⇔ x = 1 2

Найдём нули знаменателя:

x x log32 3 − 2 = 0 ⇔ 3 = 3 ⇔ x= log32 lnx = 0 ⇔ ln x= ln 1 ⇔ x= 1

По методу интервалов имеем:

$PIC$

Отсюда получаем

[ 1 1] x∈ 16;2 ∪ (log32;1)

Пересечём ответ с ОДЗ и окончательно получим

[ 1 1] x∈ 16;2 ∪ (log32;1)

Ответ:

$[0,0625;0,5]∪ (log 2;1) 3$

Ошибка.
Попробуйте повторить позже

Задача 5#512

Решите неравенство

lg2 x2 ⋅ (log22x+7(x + 7) + 3log2x+7(x + 7) + log2x+7(2x + 7 )2) -------------------------x---------------------------------≤ 0 (5 − 1) lg 2x

Показать ответ и решение

ОДЗ:

( || x2 > 0 ||| ||| 2x + 7 > 0 |||{ 2x + 7 ⁄= 1 { x > 0 | x + 7 > 0 ⇔ x ⁄= 0,5 |||| 5x − 1 ⁄= 0 ||| ||| x > 0 ( lg 2x ⁄= 0

На ОДЗ $5x − 1 > 0$ , тогда исходное неравенство на ОДЗ равносильно

lg2 x2 ⋅ (log2 (x + 7) + 3log (x + 7) + log (2x + 7 )2) ----------2x+7--------------2x+7-------------2x+7-----------≤ 0 lg 2x

На ОДЗ $2x + 7 > x + 7 > 1$ , следовательно, $log2x+7(x + 7) > 0$ , тогда на ОДЗ

log22x+7(x + 7) + 3 log2x+7 (x + 7) + log2x+7(2x + 7)2 > 0

и исходное неравенство на ОДЗ равносильно

lg2x2- lg 2x ≤ 0

Найдём нули числителя:

2 2 2 lg x = 0 ⇔ lg x = lg1 ⇔ x = ±1

Найдём нули знаменателя:

lg2x = 0 ⇔ lg2x = lg 1 ⇔ x = 0,5

По методу интервалов на ОДЗ:

$PIC$

откуда

x ∈ (0;0,5) ∪ {1}.

Ответ:

$(0;0,5) ∪ {1}$

Ошибка.
Попробуйте повторить позже

Задача 6#513

Решите неравенство

logx(x + 1) ⋅ log(x+2)(x + 3 ) ⋅ ...⋅ log (x+2n)(x + 2n + 1) ---------ln(x-+-1)-⋅ ln-(x-+-2-) ⋅ ...⋅-ln(x-+-n-)-------≤ 0

при каждом $n ∈ ℕ$ .

Показать ответ и решение

ОДЗ:

( | x > 0 |||| ||| x ⁄= 1 ||| x + 1 > 0 |||| ||| x + 2 > 0 { { x + 2 ⁄= 1 x > 0 | ⇔ ||| x + 3 > 0 x ⁄= 1 ||| ... |||| x + 2n > 0 ||| ||| x + 2n ⁄= 1 |( x + 2n + 1 > 0

По методу рационализации: на ОДЗ

logx(x-+-1) ⋅-log(x+2)(x +-3) ⋅ ...⋅ log-(x+2n)(x-+-2n-+-1)-≤ 0 ⇔ ln(x + 1) ⋅ ln(x + 2) ⋅ ...⋅ ln (x + n) (x − 1)(x + 1 − 1)(x + 2 − 1 )(x + 3 − 1) ⋅ ...⋅ (x + 2n − 1)(x + 2n + 1 − 1) ⇔ -------------------------------------------------------------------------≤ 0 ⇔ (x + 1 − 1) ⋅ ... ⋅ (x + n − 1) (x − 1)x(x + 1)(x + 2) ⋅ ...⋅ (x + 2n − 1)(x + 2n ) ⇔ ------------------------------------------------≤ 0. x ⋅ ...⋅ (x + n − 1 )

С учётом ОДЗ последнее неравенство равносильно

(x − 1) ≤ 0.

Таким образом, с учётом ОДЗ:

x ∈ (0;1).

Ответ:

$(0;1)$

Ошибка.
Попробуйте повторить позже

Задача 7#998

Решите неравенство

−|x− 2| 2 2 ⋅log2(4x− x − 2)≥ 1

Показать ответ и решение

Рассмотрим первый множитель левой части $2−|x−2|.$ Так как модуль при всех значениях $x$ неотрицателен, то

|x − 2|≥ 0 ⇒ − |x − 2|≤ 0

Следовательно,

2−|x−2| ≤20 =1

Рассмотрим второй множитель $log(4x− x2− 2). 2$ Выделим полный квадрат:

4x − x2− 2 = −(x2− 4x+ 4)+2 = −(x− 2)2 +2

Так как квадрат любого выражения — число неотрицательное, то

(x − 2)2 ≥ 0 ⇒ − (x − 2)2 ≤ 0 ⇒ − (x − 2)2+ 2≤ 2

Следовательно,

log2(4x− x2− 2)≤ log22 = 1

Получили, что оба множителя в левой части $≤ 1,$ а значит и их произведение $≤ 1.$

Значит, неравенство будет иметь решения тогда и только тогда, когда оба они равны по 1.

Таким образом, получаем, что $x = 2$ — единственное решение неравенства.

Ответ:

${2}$

Ошибка.
Попробуйте повторить позже

Задача 8#1072

Решите неравенство

( 2 ) ( 2 ) log(sinx+cosx+4) x + 1 ≥ log(2sinx⋅cosx+4,5) x + 1

Показать ответ и решение

Выпишем ОДЗ:

(| sinx +cosx +4 >0 |||| |{ sin2x +cosx +4 ⁄=1 || x + 1> 0 ||||( 2sinx cosx + 4,5> 0 2sinx cosx + 4,5⁄= 1

Так как по формуле вспомогательного аргумента

(√ - √- ) sinx+ cosx= √2- --2sin x+ -2-cosx = √2 sin(x + π), 2 2 4

а по формуле двойного угла $2sinxcosx =sin2x,$ то

( ( ) √ - |||sin x+ π- > −2 2 |||| ( 4) √- {sin x+ π- ⁄= − 3 2 ⇔ x ∈ℝ ||| 4 2 ||||(sin 2x> −4,5 sin 2x⁄= −3,5

Заметим, что при одинаковых аргументах один логарифм будет $≥$ другого логарифма в одном из двух случаев:

1.

Аргументы этих логарифмов равны 1. Тогда

x2+ 1= 1 ⇒ x = 0

Тогда неравенство принимает вид:

log(sinx+cosx+4)1 ≥log(2sinx⋅cosx+4,5)1,

что на ОДЗ равносильно

0≥ 0,

что является верным неравенством. Следовательно, $x= 0$ является решением неравенства.

2.

$x⁄= 0.$ Заметим, что функция $f(x)= logxa$ является убывающей при $a > 1$ и возрастающей при $a < 1.$ В нашем случае $2 x +1 > 1,$ следовательно, функция убывает. Значит, чем больше значение функции, тем меньше значение $x.$ Следовательно, при $x⁄= 0$ неравенство равносильно

( 2 ) ( 2 ) log(sinx+cosx+4) x + 1 ≥ log(2sinx⋅cosx+4,5) x + 1 sinx+ cosx+ 4≤ 2sin xcosx+ 4,5 ( 1) (1− 2cosx) sinx − 2 ≤0 ( ) ( ) cosx− 1 sin x− 1 ≥ 0 2 2

Данное неравенство равносильно совокупности систем:

⌊(| 1 ||{ sinx ≥ 2 |||( cosx ≥ 1 || 2 ||(| 1 ||{ sinx ≤ 2 ⌈|( cosx ≤ 1 2

Решим каждую систему по окружности. Первая система:

$PIC$

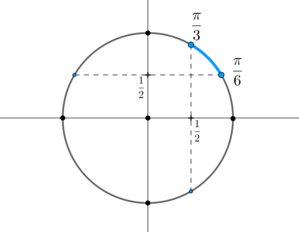
Вторая система:

$PIC$

Тогда ответом будут

[ ] [ ] x ∈ π-+ 2πk; π+ 2πk ∪ 5π +2πk; 5π + 2πk , k ∈ ℤ 6 3 6 3

Тогда окончательный ответ — это объединение решений обоих случаев, то есть

[π π ] [5π 5π ] x ∈ 6-+ 2πk;3 + 2πk ∪ 6- +2πk;-3 + 2πk ∪{0}, k ∈ℤ

Ответ:

$[ ] x ∈[π-+ 2πk; π-+2πk]∪ 5π +2πk; 5π + 2πk ∪ {0}, k ∈ℤ 6 3 6 3$

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	2

Обоснованно получен ответ, отличающийся от верного исключением/включением граничных точек,	1
ИЛИ
получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	2

При этом в первом случае выставления 1 балла допускаются только ошибки в строгости неравенства: « $<$ » вместо « $≤$ » или наоборот. Если в ответ включено значение переменной, при котором одна из частей неравенства не имеет смысла, то выставляется оценка «0 баллов».

Ошибка.
Попробуйте повторить позже

Задача 9#1233

Решите неравенство

9x2−4 9x2- ( (3 )log32x+12) -4-- 44 − 2x + 1 ≤ 3

Показать ответ и решение

Найдем ОДЗ неравенства:

( |{3x + 1> 0 ( 2 ) |23 ⇔ x∈ − 3;0 ∪ (0;+ ∞ ) (2x + 1⁄= 1

Решим неравенство на ОДЗ. Так как по основному логарифмическому свойству $alogab = b$ , то

49x24-− 2 9x42−1 ≤ 3

Сделаем замену $2 t =2 9x4--$ , $t> 0$ , тогда

( 3) [ 3 ] t2− 0,5t− 3≤ 0 ⇔ t+ 2 (t− 2)≤ 0 ⇔ t∈ − 2;2

Так как согласно замене $t> 0$ , то получаем $0 <t ≤2$ . Сделаем обратную замену:

9x2- 9x2 ( 2) ( 2) 0< 2 4 ≤ 2 ⇔ -4-≤ 1 ⇔ x− 3 x + 3 ≤ 0 ⇔ [ ] 2 2 x∈ −3;3

Пересечем ответ с ОДЗ и получим

( 2 ) ( 2 ] x ∈ −3;0 ∪ 0;3

Ответ:

$( 2 ) ( 2] −3 ;0 ∪ 0;3$

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	2

Обоснованно получен ответ, отличающийся от верного исключением/включением граничных точек,	1
ИЛИ
получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	2

При этом в первом случае выставления 1 балла допускаются только ошибки в строгости неравенства: « $<$ » вместо « $≤$ » или наоборот. Если в ответ включено значение переменной, при котором одна из частей неравенства не имеет смысла, то выставляется оценка «0 баллов».

Ошибка.
Попробуйте повторить позже

Задача 10#1816

Решите неравенство

(2x + 15)log (x2 + 7x) ≤ 0 x+2

Показать ответ и решение

ОДЗ:

( | x + 2 > 0 { | x + 2 ⁄= 1 ⇔ x > 0 ( x2 + 7x > 0

На ОДЗ $2x + 15 > 0$ , $x + 2 > 1$ , следовательно, исходное неравенство на ОДЗ равносильно

2 2 logx+2(x + 7x) ≤ logx+2 1 ⇔ x + 7x − 1 ≤ 0

По методу интервалов:

$PIC$

откуда $[ √ --- √---] − 7-−--53- −-7 +--53- x ∈ 2 ; 2$ .
Пересечём ответ с ОДЗ:

( √ --] x ∈ 0; −-7-+--53 2

Ответ:

$√ --- (0;− 3,5 + 0,5 53]$

Ошибка.
Попробуйте повторить позже

Задача 11#1818

Решите неравенство

x log π (x + 3 ) ≤ 0 x+2

Показать ответ и решение

ОДЗ:

( | x + π-> 0 ( π |{ 2π { x > − -- x + --⁄= 1 ⇔ 2π ||( 2 ( x ⁄= − --+ 1 x + 3 > 0 2

Заметим, что

x + 3 > x + π- + 1 2

Рассмотрим два случая:
1) $x > − π-+ 1 2$ , тогда

π logx+ 2(x + 3) > 0

и исходное неравенство равносильно

x ≤ 0,

то есть в этом случае подходят

( ] x ∈ − π-+ 1;0 2

2) $π π − --< x < − --+ 1 2 2$ , тогда

logx+ π2(x + 3) < 0

и исходное неравенство равносильно

x ≥ 0,

то есть в этом случае подходящих $x$ нет.
В итоге ответ с учётом ОДЗ:

( π ] x ∈ − --+ 1;0 . 2

Ответ:

$( π ] − --+ 1;0 2$

Ошибка.
Попробуйте повторить позже

Задача 12#1819

Решите неравенство

x+1 x log5x25 + log25x+1 5 − 2 > 0

Показать ответ и решение

Найдем ОДЗ неравенства:

( x |||{ 5x> 0 5 ⁄= 1 ⇔ x ∈(− ∞;−1)∪ (−1;0)∪(0;+∞ ) |||( 25x+1 > 0 25x+1 ⁄= 1

Сделаем замену $x+1 log5x25 = y$ :

{ 1 y2−-2y+-1 (y−-1)2- y >0 y+ y − 2> 0 ⇔ y >0 ⇔ y > 0 ⇔ y ⁄=1,

откуда

{ x+1 ({ 2x+-2 > 0 log5x25x+1 > 0 ⇔ 2xx+ 2 log5x25 ⁄= 1 ( --x-- ⁄= 1

Решая первое неравенство последней системы, получаем

x ∈ (− ∞;− 1) ∪(0;+ ∞ )

Решая второе неравенство последней системы, получаем

x∈ (−∞; −2)∪(− 2;0)∪ (0;+∞ )

В итоге

x ∈(−∞; −2)∪ (− 2;−1)∪(0;+∞ )

– входит в ОДЗ

Ответ:

$(−∞; −2)∪ (− 2;− 1)∪(0;+∞ )$

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	2

Обоснованно получен ответ, отличающийся от верного исключением/включением граничных точек,	1
ИЛИ
получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	2

При этом в первом случае выставления 1 балла допускаются только ошибки в строгости неравенства: « $<$ » вместо « $≤$ » или наоборот. Если в ответ включено значение переменной, при котором одна из частей неравенства не имеет смысла, то выставляется оценка «0 баллов».

Ошибка.
Попробуйте повторить позже

Задача 13#1820

Решите неравенство

2x+log2(1+x1ln2) ≥ 1

Показать ответ и решение

ОДЗ:

----1---- > 0 ⇔ 1 + x ln 2 > 0 ⇔ x > − -1-. 1 + x ln 2 ln 2

На ОДЗ:
исходное неравенство равносильно неравенству

x log (--1- ) x 1 x 2 ⋅ 2 21+xln2 ≥ 1 ⇔ 2 ⋅--------- ≥ 1 ⇔ 2 ≥ 1 + xln 2 ⇔ x 1 + x ln 2 ⇔ 2 − 1 − xln 2 ≥ 0.

Рассмотрим функцию

f(x ) = 2x − 1 − x ln2.

Найдём её промежутки возрастания/убывания:

f′(x) = 2x ln 2 − ln 2 = ln2 ⋅ (2x − 1)

Легко проверить, что $x = 0$ – единственная точка локального минимума функции $f$ , тогда она является точкой минимума $f$ и наименьшее значение $f$ равно

0 f(0) = 2 − 1 − 0 ⋅ ln 2 = 0.

Таким образом, $x 2 − 1 − xln2 ≥ 0$ – верно при всех $x ∈ ℝ$ , тогда ответ совпадает с ОДЗ:

x > − -1--. ln2

Ответ:

$( ) − -1--;+ ∞ ln 2$

Ошибка.
Попробуйте повторить позже

Задача 14#2422

Решите неравенство

( )log (2x+3) 3log2(x2)+ 2⋅|x|log29 ≤ 3⋅ 1 0,5 3

Показать ответ и решение

Запишем ОДЗ:

{ x2 >0 ⇒ x∈ (−1,5;0)∪ (0;+∞ ) 2x +3 > 0

Тогда на ОДЗ второе слагаемое левой части можно преобразовать так:

( ) ( ) 2⋅|x|log29 = 2 ⋅|x|log23 2 = 2 ⋅3log2|x| 2 = 2⋅3log2x2

Правую часть можно преобразовать так:

( −1)log0,5(2x+3) − log0,5(2x+3) log2(2x+3) 3⋅ 3 = 3⋅3 = 3⋅3

Тогда все неравенство перепишется в виде

log x2 logx2 log(2x+3) log x2 log(2x+3) 3 2 + 2⋅3 2 ≤3 ⋅3 2 ⇒ 3 2 ≤ 3 2 ⇒

⇒ log2x2 ≤ log2(2x+ 3) ⇒ x2 ≤ 2x+ 3

Получили квадратичное неравенство

x2− 2x− 3≤ 0 ⇒ x∈ [−1;3]

Пересекая полученное множество с ОДЗ, получим

x∈ [−1;0) ∪(0;3]

Ответ:

$[−1;0)∪(0;3]$

Ошибка.
Попробуйте повторить позже

Задача 15#2722

Найдите все такие $x ∈ ℝ$ , которые являются решениями неравенства

N ⋅ log 3 ⋅ log (1 + x) ≥ 1 (1+Nx) 3

при любых $N ∈ ℕ.$

Показать ответ и решение

ОДЗ:

( |{ 1 + N x > 0 |( 1 + N x ⁄= 1 — при лю бы х N ∈ ℕ 1 + x > 0

Покажем, что $x < 0$ не подходят по ОДЗ:
зафиксируем произвольное $x < 0$ , тогда $− x > 0$ . Существует $n ∈ ℕ$ , такое что

1 n > ----. − x

Положим $N = n$ , тогда

N > -1-- ⇒ − xN > 1 ⇒ 1 + N x < 0, − x

что не подходит по ОДЗ. Таким образом, $x ≥ 0$ .

Также по ОДЗ не подходит $x = 0$ , а $x > 0$ подходят по ОДЗ, следовательно,
ОДЗ:

x > 0.

На ОДЗ:
исходное неравенство равносильно неравенству

-----1-------⋅ log (1 + x)N ≥ 1 log3(1 + N x ) 3

Так как на ОДЗ

1 + N x > 1,

то $log3(1 + N x) > 0$ , следовательно,

------1------ N N log (1 + N x) ⋅ log3(1 + x) ≥ 1 ⇔ log3(1 + x) ≥ log3(1 + N x) ⇔ 3 N ⇔ (1 + x ) ≥ (1 + N x).

Зафиксируем произвольный $x > 0$ .
Докажем по индукции, что данное неравенство выполнено для всех $N ∈ ℕ$ :

1) $N = 1$ :

1 + x ≥ 1 + x

– верно.

2) Рассмотрим произвольное $m ∈ ℕ$ , такое что $(1 + x)m ≥ 1 + mx$ , тогда

m+1 m 2 (1 + x) = (1 + x) ⋅ (1 + x) ≥ (1 + x) ⋅ (1 + mx ) = 1 + mx + x + mx ≥ 1 + x(m + 1),

таким образом, мы доказали, что рассматриваемый $x$ подходит. Так как мы фиксировали произвольный $x > 0$ , то все $x > 0$ являются решениями исходной задачи.

Ответ:

$(0;+ ∞ )$

Ошибка.
Попробуйте повторить позже

Задача 16#15708

Решите неравенство

∘ ----- x+ 1⋅log0,5(log2|1− x|)≥ 0 2

Показать ответ и решение

При $x = −0,5$ левая часть неравенства имеет смысл и равна нулю. Тогда $x = −0,5$ пойдет в ответ.

При условии $x> − 0,5$ получаем неравенство

log (log |1 − x|)≥ 0 0,5 2

Отсюда имеем:

0< log2 |1− x|≤ 1 ⇒ 1< |1− x|≤ 2

Следовательно, $− 1 ≤x < 0$ или $2< x ≤3.$

Учитывая условие $x > −0,5,$ находим:

1 − 2< x< 0 или 2< x ≤3

Объединяя полученные множества c $x = −0,5,$ получаем

[ ) x ∈ − 1;0 ∪(2;3] 2

Ответ:

$[ ) − 1;0 ∪(2;3] 2$

Ошибка.
Попробуйте повторить позже

Задача 17#15913

Решите неравенство

xlog2x + 16x− log2x < 17

Показать ответ и решение

ОДЗ: $x > 0.$

Решим неравенство на ОДЗ.

Сделаем замену $t = xlog2x = elnx⋅log2x > 0$ .

Тогда

16 t2-−-17t+-16 t+ t < 17 ⇔ t < 0

Решая неравенство методом интервалов, получим:

[ t < 0 1 < t < 16

Так как из-за замены $t > 0$ , то неравенство $t < 0$ не имеет решений.

Делаем обратную замену:

lnx⋅logx 0 lnx⋅log x ln 16 1 < e 2 < 16 ⇔ e < e 2 < e ⇔ 0 < lnx ⋅log2x < ln16

Решим данное двойное неравенство как два неравенства по отдельности и затем пересечем решения.

1) $ln x⋅log2x > 0.$ Решим с помощью метода рационализации:

2 (e− 1)(x − 1)(2 − 1)(x− 1) > 0 ⇔ (x − 1) > 0 ⇔ x ⁄= 1

2) $ln x⋅log2x < ln16$ . Разделим обе части неравенства на положительное число $ln16$ :

lnx-⋅log x < 1 ⇒ log x⋅log x < 1 ⇒ ln 16 2 16 2 1(log x )2 < 1 ⇒ (log x)2 < 4 ⇒ 4 2 2 − 2 < log x < 2 ⇒ 1< x < 4 2 4

Пересекая решения этих двух неравенств между собой и с ОДЗ, получаем окончательный ответ.

Ответ:

$(0,25;1) ∪(1;4)$

Ошибка.
Попробуйте повторить позже

Задача 18#17142

Решите неравенство

log1log3(−2x) log1log5(−2x) 5 5 < 3 3

Показать ответ и решение

По свойствам логарифма исходное неравенство равносильно:

$pict$

Последний переход корректен, так как первое неравенство системы выполняется при всех $x$ из ОДЗ: $− 2x> 1,$ ведь основание логарифма левой части больше основания логарифма правой части, а аргументы равны.

Ответ:

$(−∞; −0,5)$

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	2

Обоснованно получен ответ, отличающийся от верного исключением/включением граничных точек,	1
ИЛИ
получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	2

При этом в первом случае выставления 1 балла допускаются только ошибки в строгости неравенства: « $<$ » вместо « $≤$ » или наоборот. Если в ответ включено значение переменной, при котором одна из частей неравенства не имеет смысла, то выставляется оценка «0 баллов».

Ошибка.
Попробуйте повторить позже

Задача 19#17246

Решите неравенство

( 35 x−1 x− 1) 2x≥ log2 3-⋅6 − 2⋅9 2

Показать ответ и решение

Преобразуем неравенство:

$pict$

Из второго неравенства получаем

35 ⋅2x− 2⋅3x > 0 6 (2)x 12 3 > 35 x< log212 335

Из первого неравенства имеем:

( ) ( ) 2 2x 2 x 18⋅ 3 − 35 ⋅ 3 +12 ≥0

Сделаем замену $( 2)x t = 3 :$

2 18 ⋅t − 35t+ 12≥ 0 ( ] [ ) t∈ −∞; 4 ∪ 3;+∞ 9 2

Сделаем обратную замену:

( ) ⌊ 2 x 4 ||(3 ) ≤ 9 ⌈ 2 x 3 3 ≥ 2

Отсюда получаем

x ∈(− ∞;−1]∪ [2;+∞ )

Далее имеем:

( )2 2 = 4 = 4⋅35= 140-> 108= 9-⋅12 = 12 3 9 9⋅35 315 315 9 ⋅35 35

Тогда так как основание логарифма меньше 1, то получаем

12 4 log2335 > log23 9 = 2

Поскольку $x < log2 12-, 3 35$ то окончательно имеем:

[ ) x ∈ (− ∞;−1]∪ 2;log212 335

Ответ:

$[ 12) (−∞; −1]∪ 2;log2335$

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	2

Обоснованно получен ответ, отличающийся от верного исключением/включением граничных точек,	1
ИЛИ
получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	2

При этом в первом случае выставления 1 балла допускаются только ошибки в строгости неравенства: « $<$ » вместо « $≤$ » или наоборот. Если в ответ включено значение переменной, при котором одна из частей неравенства не имеет смысла, то выставляется оценка «0 баллов».

Ошибка.
Попробуйте повторить позже

Задача 20#23600

Решите неравенство:

1 9log (7− x) log2(x−7)2 32 ⋅2 16 ≥ 2 16 .

Показать ответ и решение

1 9log (7−x) log2 (x−7)2 32 ⋅2 16 ≥ 2 16

Найдем ОДЗ данного неравенства:

( { 7− x> 0 ( (x − 7)2 > 0 ⇔ 7 − x > 0 ⇔ x< 7

Преобразуем левую часть неравенства:

1- 9log16(7−x) −5 9log24(7− x) 94 log2(7−x)−5 32 ⋅2 = 2 ⋅2 = 2

Преобразуем показатель степени в правой части неравенства:

2 1 log216(x − 7)2 = (2log24|x − 7|)2 = (4 log2|7− x|)2 = 4 log22|x− 7|

На ОДЗ $|x− 7|= 7− x$ и исходное неравенство примет вид:

94log2(7−x)− 5 14log22(7−x) 9 1 2 2 ≥ 2 ⇔ 4 log2(7− x)− 5≥ 4 log2(7 − x)

Обозначим $t =log2(7− x)$ , тогда $2 2 log2(7− x)= t$

Перепишем неравенство в виде

$pict$

Решим неравенство методом интервалов:

$PIC$

t∈ [4;5] ⇔ 4 ≤t ≤5

Произведем обратную замену:

4 ≤log2(7− x)≤ 5 ⇔ 24 ≤ 7 − x ≤ 25 ⇔ 16 ≤ 7− x≤ 32 ⇔ 9≤ − x≤ 25 ⇔ −25 ≤x ≤ −9

Учтем ОДЗ:

( { x< 7 ( −25 ≤x ≤ −9 ⇔ − 25 ≤ x≤ −9 ⇔ x ∈ [−25;−9]

Ответ: $[− 25;− 9]$

Ответ:

$[−25;−9]$

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	2

Обоснованно получен ответ, отличающийся от верного исключением/включением граничных точек,	1
ИЛИ
получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	2

При этом в первом случае выставления 1 балла допускаются только ошибки в строгости неравенства: « $<$ » вместо « $≤$ » или наоборот. Если в ответ включено значение переменной, при котором одна из частей неравенства не имеет смысла, то выставляется оценка «0 баллов».

15.10 Смешанные неравенства