1.24 Теорема синусов и теорема косинусов
Ошибка.
Попробуйте повторить позже
В треугольнике
— точка пересечения серединных перпендикуляров к сторонам
и
—
серединный перпендикуляр к стороне
Найдите
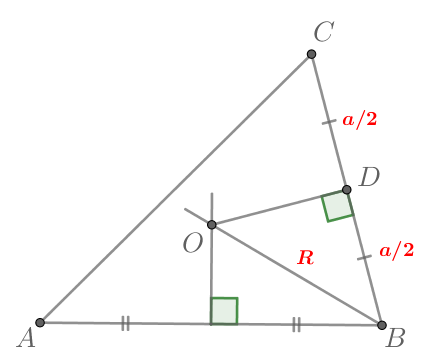
Так как — точка пересечения серединных перпендикуляров в треугольнике
то
— центр описанной около
окружности,
Обозначим По теореме Пифагора
По теореме синусов
Тогда
Значит,
Так как
то
Ошибка.
Попробуйте повторить позже
В треугольнике
— точка пересечения серединных перпендикуляров к сторонам
и
—
серединный перпендикуляр к стороне
Найдите
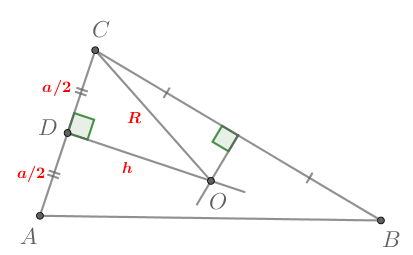
Так как — точка пересечения серединных перпендикуляров в треугольнике
то
— центр описанной около
окружности,
Обозначим
По теореме Пифагора
По теореме синусов
Тогда
Так как
то
Ошибка.
Попробуйте повторить позже
В треугольнике
— точка пересечения серединных перпендикуляров к сторонам
и
— серединный
перпендикуляр к стороне
Найдите
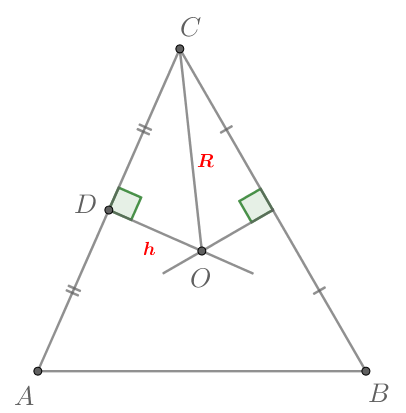
Так как — точка пересечения серединных перпендикуляров в треугольнике
то
— центр описанной около
окружности,
Обозначим тогда
По теореме Пифагора
По теореме синусов
Тогда следовательно,
Ошибка.
Попробуйте повторить позже
Площадь остроугольного треугольника равна
Найдите
если сторона
равна 8, а медиана
равна
5.
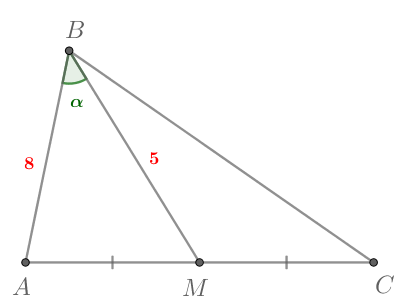
Т.к. — медиана, то она делит треугольник
на два равновеликих треугольника:
с учетом остроугольности
Воспользуемся теоремой косинусов и найдем
Ошибка.
Попробуйте повторить позже
В треугольнике
— точка пересечения серединных перпендикуляров к сторонам
и
— серединный
перпендикуляр к стороне
Найдите
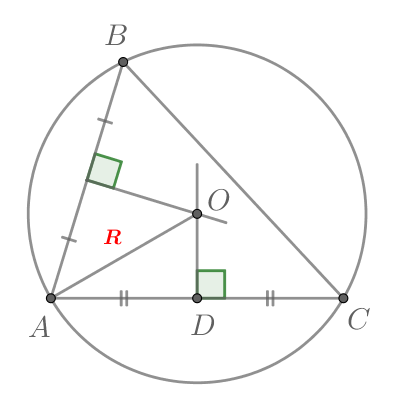
Так как — точка пересечения серединных перпендикуляров в треугольнике
то
— центр описанной около
окружности,
По теореме Пифагора:
По теореме синусов
Следовательно, Так как
то
Ошибка.
Попробуйте повторить позже
Сторона тупоугольного треугольника
равна радиусу описанной около него окружности. Найдите угол
Ответ дайте в
градусах.
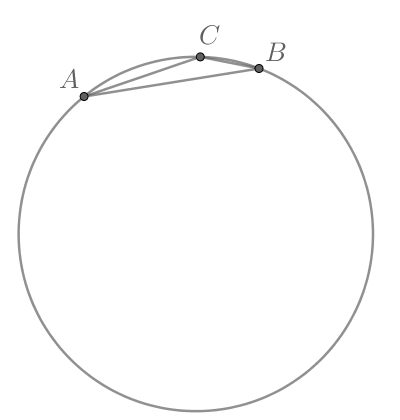
Пусть По теореме синусов:
Так как тупой, то
Ошибка.
Попробуйте повторить позже
Сторона правильного треугольника равна Найдите радиус окружности, описанной около этого треугольника.

По теореме синусов
где — сторона треугольника,
— противолежащий этой стороне угол,
— радиус описанной окружности. Так как в
правильном треугольнике все углы равны по
то
Ошибка.
Попробуйте повторить позже
Радиус окружности, описанной около правильного треугольника, равен Найдите сторону этого треугольника.

По теореме синусов
где — сторона треугольника,
— противолежащий этой стороне угол,
— радиус описанной окружности. Так как в
правильном треугольнике все углы равны по
то
Ошибка.
Попробуйте повторить позже
Боковая сторона равнобедренного треугольника равна 1, угол при вершине, противолежащей основанию, равен Найдите
диаметр описанной окружности этого треугольника.
По теореме косинусов
Следовательно, По теореме синусов
где — сторона треугольника,
— противолежащий этой стороне угол,
— радиус описанной окружности.
Следовательно,
Ошибка.
Попробуйте повторить позже
В треугольнике
Найдите
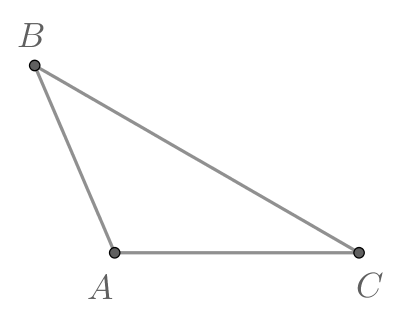
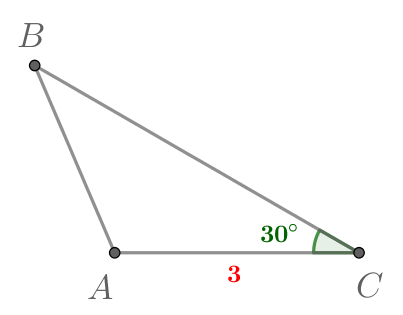
По теореме синусов
где — радиус описанной около
окружности.
Тогда
Значит, откуда
Ошибка.
Попробуйте повторить позже
В треугольнике
Найдите
если известно, что
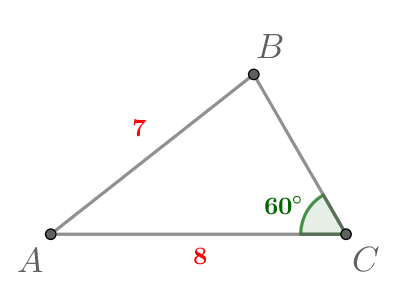
По теореме косинусов
Обозначим за
тогда
откуда получаем
Так как то подходит
Итого:
Ошибка.
Попробуйте повторить позже
В треугольнике
радиус описанной около
окружности равен 5. Найдите
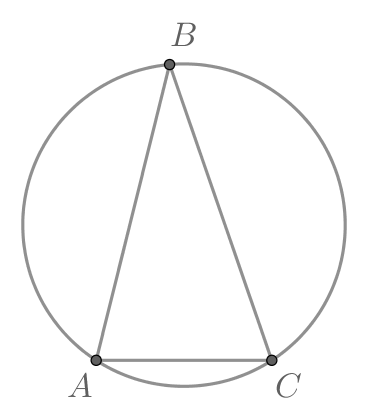
По теореме синусов
где — радиус описанной около
окружности.
Тогда
Значит, откуда
Ошибка.
Попробуйте повторить позже
В треугольнике
— точка пересечения серединных перпендикуляров к сторонам
и
—
серединный перпендикуляр к стороне
Найдите
Ответ дайте в градусах.

Так как — точка пересечения серединных перпендикуляров в треугольнике
то
— центр описанной около
окружности,
По теореме Пифагора
По теореме синусов
Следовательно, или
но
а в треугольнике против большего угла лежит большая сторона, тогда
Ошибка.
Попробуйте повторить позже
— диаметр окружности с центром
который пересекает хорду
в точке
лежащей на
Градусная мера дуги
равна
Найдите
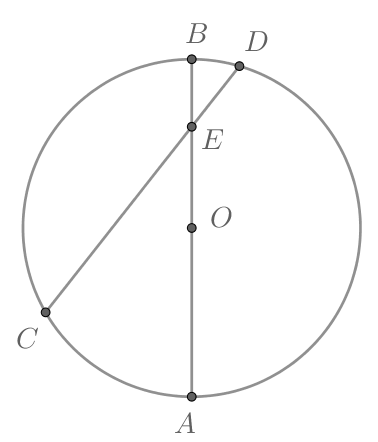
Построим радиус и отрезок
тогда
и, следовательно, треугольник
— равносторонний,
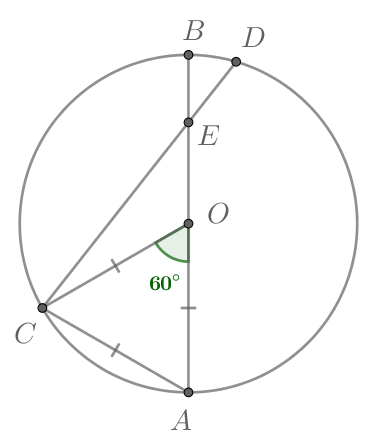
Запишем теорему косинусов для треугольника
Тогда
Значит,
По теореме синусов
Тогда
Из основного тригонометрического тождества находим: Так как точка
лежит на
то
—
острый, значит
Ошибка.
Попробуйте повторить позже
— вписанный четырёхугольник, причём
Найдите
Обозначим
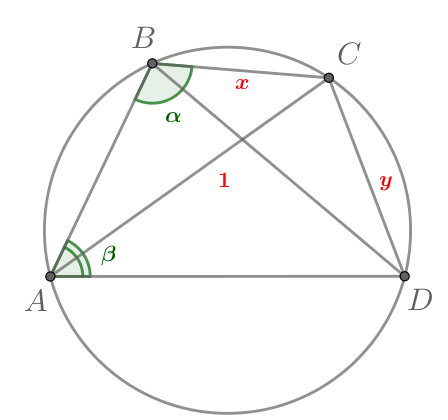
Выразим при помощи теоремы косинусов в треугольниках
и
Так как то
Складывая два последних равенства с учётом того, что получим:
Выразим при помощи теоремы косинусов в треугольниках
и
Тогда
Так как то
В итоге
Ошибка.
Попробуйте повторить позже
— вписанный четырёхугольник, причём
Найдите
если
Обозначим

Выразим при помощи теоремы косинусов в треугольниках
и
Так как то
Складывая два последних равенства с учётом того, что получим:
Выразим при помощи теоремы косинусов в треугольниках
и
Тогда
Так как то
В итоге
Обозначим
Так как то
тогда
откуда
следовательно,
(
).
Ошибка.
Попробуйте повторить позже
Найдите площадь треугольника если сторона
медиана
Из треугольника найдем
по теореме косинусов:
Значит,
Так как — медиана, то она делит треугольник
на два равновеликих треугольника:
Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике сторона
которого равна 12, на стороны
и
опущены высоты
и
Вычислите площадь четырехугольника
если известно, что площадь треугольника
равна 2, а радиус окружности,
описанной около треугольника
равен

По теореме синусов и по основному тригонометрическому тождеству имеем:
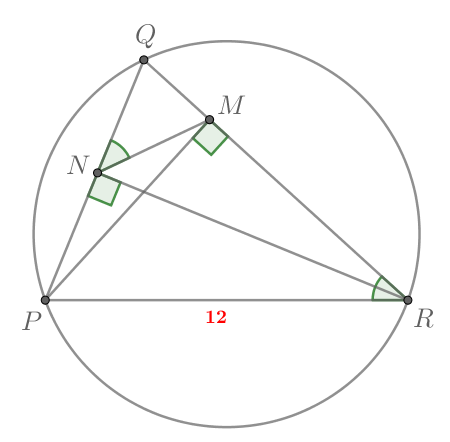
Далее, так как то треугольник
подобен треугольнику
по двум углам, тогда
имеем:
Ошибка.
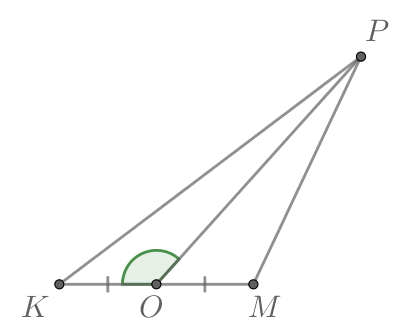
Попробуйте повторить позже
В треугольнике проведена медиана
Найдите площадь треугольника
если
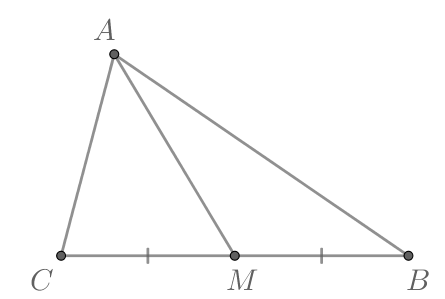

Из треугольника по теореме косинусов найдем
Т.к. — медиана, то она делит треугольник
на два равновеликих треугольника:
Ошибка.
Попробуйте повторить позже
Радиус окружности, описанной около треугольника равен
Большая сторона треугольника
равна 10, а
Найдите
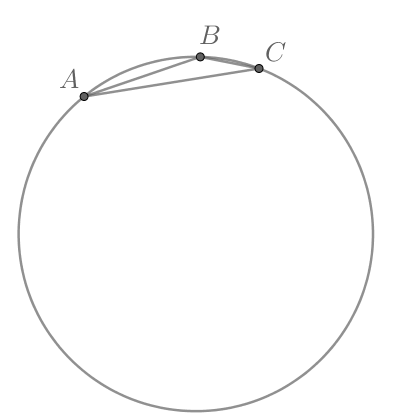
В треугольнике против большего угла лежит большая сторона, тогда По теореме синусов
откуда



