Тема Региональные этапы ВСОШ прошлых лет

Региональные этапы ВСОШ прошлых лет

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#95210

Фирма М продает некое лекарство в две страны - А и В. Фирма является монополистом на мировом рынке данного лекарства, так как она обладает патентом на его производство. В стране А спрос описывается уравнением $QA = 30− PA$ , а в стране В уравнением $QB = 10− PB$ . Издержки производства считайте равными нулю. Фирма может назначать разные цены в разных странах, так как покупка лекарств иностранцами и перепродажи эффективно блокируются.
a) (10 баллов) Найдите цены $P ⋆ A$ и $P⋆ B$ , которые назначит фирма в отсутствие вмешательства государства.
б) (20 баллов) Президент страны А, ратуя за доступность лекарств, ввел следующее правило: фирма M не может назначать цену в стране А выше, чем в стране В. Теперь фирма M назначает цены так, чтобы прибыль была максимальная с учетом этого правила. Удастся ли президенту с помощью этой меры добиться снижения цены в своей стране?

Показать ответ и решение

a) Составим функцию прибыли:

π = (30− PA)PA + (10 − PB )PB

Эта функция - сумма двух не зависящих друг от друга парабол с ветвями вниз, значит, ее значение будет максимально, когда максимума достигает каждая из парабол. Это происходит при $P⋆A =15$ и $P ⋆B = 5$ .

б) В пункте а) цена в стране А оказалась выше, поэтому максимизировать прибыль так, как раньше, фирма не сможет. Она будет назначать одинаковые цены на двух рынках, то есть фактически столкнется с общей функцией спроса:

{ 30 − P, если 10 ≤P ≤ 30 Q = 40 − 2P, если 0 ≤ P ≤ 10.

Функция прибыли имеет вид:

{ (30− P )P, если 10 ≤P ≤ 30; π = (40− 2P)P, если 0 ≤P ≤ 10.

На первом участке фирма работает только на рынке страны А. Как и в предыдущем пункте, оптимальная цена в стране А при этом равна 15, а прибыль равна 225.

На втором участке ( $P ≤ 10$ ) фирма обслуживает рынки в обеих странах. Парабола $(40− 2P)P$ имеет ветви вниз и максимум в точке $P = 10$ , прибыль при этом равна 200 , то есть меньше, чем в предыдущем случае. Можно также заметить, что при такой цене фирма ничего не продает на рынке страны B, а на рынке страны А не получает максимальной прибыли.

Следовательно, цена в обеих странах будет 15. Таким образом, цена в стране А не изменится, президент своей цели не добьется.

Ответ:

а) $P ⋆A = 15,P⋆B = 5$

б) Нет, не удастся

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#95222

Спрос на рынке авиаперевозок описывается уравнением $Qd = 20− P$ , а предложение - уравнением $Qs = P∕3$ . Выбросы двигателей самолетов загрязняют воздух и вносят вклад в парниковый эффект. Вред от этого зависит от объема перевозок и составляет $2 aQ$ д. е., где $a> 0$ . Школьница Грета Т. считает, что данный внешний эффект нужно скорректировать с помощью потоварного налога на авиаперевозки, такого, при котором цена для потребителей вырастет на $20%$ . Расчеты экономистов, однако, показали, что при введении такого налога величина общественного благосостояния не только не увеличится, но и уменьшится на $20%$ .
a) (10 баллов) Определите значение ставки потоварного налога $t$ , при котором цена для потребителей вырастет так, как хочет Грета.
б) (10 баллов) Определите значение параметра $a$ , при котором верны расчеты экономистов.
в) (10 баллов) Определите значение ставки потоварного налога $t⋆$ , при котором общественное благосостояние будет максимально.

Для справки. Величина общественного благосостояния при объеме $Q$ здесь равна сумме излишка потребителей (равного $2 CS = 0,5Q$ д. е.), излишка производителей после уплаты потоварного налога (равного $2 PS = 1,5Q$ д. е.) и величины налоговых сборов за вычетом вреда от выбросов.

Показать ответ и решение

a) Без налога равновесная цена определяется из уравнения $20− P =P ∕3$ , откуда $P = 15$ . Пусть введен потоварный налог по ставке $t$ . Тогда новая цена потребителей удовлетворяет уравнению $20− Pd =(Pd− t)∕3$ . Новая цена потребителей должна равняться $15⋅1,2 = 18$ , значит $20− 18 = (18 − t)∕3,t= 12$ .

б) Рассчитаем величину общественного благосостояния до и после введения налога. Налоговые поступления равны $T = tQ$ . Графическая иллюстрация представлена на рисунке.

$PIC$

Рис. 1 Излишки

До введения налога объем равен $Q0 =20 − 15 =5$ , и величина общественного благосостояния равна $0,5Q20+ 1,5Q20+ 0− aQ20 = 50− 25a$ .

После введения налога объем равен $Q1 = 20− 18= 2$ , общественное благосостояние составляет $0,5Q21+ 1,5Q21+ tQ1 − aQ21 = 8+ 24− 4a= 32− 4a$ .

Поскольку благосостояние падает на $20%$ , имеем уравнение $32− 4a= 0,8(50− 25a)$ , откуда $a = 0,5$ .

в) Чтобы получить равновесный объем $Q$ , нужно ввести налог по ставке $t(Q)=$ $= Pd(Q )− Ps(Q) =20 − Q − 3Q = 20 − 4Q$ . Сборы при этом составят $Q (20− 4Q )$ . Значит, величина общественного благосостояния при объеме $Q$ составляет

W (Q)= 0,5Q2 + 1,5Q2+ Q (20− 4Q)− aQ2 = 20Q − 2,5Q2

Промаксимизируем эту величину по $Q$ , а затем найдем ставку налога $t(Q)$ , реализующую этот объем. $W (Q)$ задает квадратичную параболу с ветвями вниз, максимум достигается в вершине параболы $Q⋆ = 20∕5 = 4$ . Этот объем реализует ставка налога $t(4)= 4$ .

Ответ:

а) $t =12$

б) $a= 1∕2$

в) $t⋆ = 4$

Ошибка.
Попробуйте повторить позже

Задача 3#95241

В закрытой экономике потребители в каждом году расходуют $60%$ от своего располагаемого дохода, а также тратят еще 10 д. е., составляющих автономное потребление. Инвестиции, совершаемые в каждый год в данной стране, зависят от настроений инвесторов, которые в свою очередь зависят от изменения ВВП за год: $It = 30+ 0,15⋅ΔYt$ , где $ΔYt = Yt− Yt−1$ . Госзакупки постоянны и равны 60 д. е. Налогов и трансфертов нет.
a) (8 баллов) Найдите уровень ВВП в долгосрочном равновесии $⋆ Y$ , то есть такой, который, единожды установившись в данной экономике, закрепится и не будет меняться без внешних шоков.
б) (8 баллов) Предположим, что в 2019 году (при $t= 2019$ ) экономика находилась в долгосрочном равновесии. В начале 2020 года правительство реализует стимулирующую фискальную политику и меняет ежегодную величину госзакупок на $10%$ . Найдите новый уровень ВВП в долгосрочном равновесии $Y ⋆⋆$ .
в) (14 баллов) Прежде чем принять значение $Y⋆⋆$ , ВВП будет динамически меняться. Найдите «краткосрочное» значение ВВП, которое будет наблюдаться в 2020 году.

Показать ответ и решение

a) В долгосрочном равновесии $ΔY = 0$ , то есть $I =30$ . Воспользовавшись формулой ВВП по расходам для закрытой экономики, составим уравнение:

Y = C + I + G Y = (0,6Y + 10)+ 30+ 60 ⋆ Y = 250

б) Поскольку политика стимулирующая, госзакупки должны увеличиться на $10%$ , то есть на 6. Составим уравнение с новым уровнем госзакупок:

Y = (0,6Y + 10)+30 +66; Y⋆⋆ = 265.

Этот же ответ можно получить, воспользовавшись формулой мультипликатора госрасходов (в которой тоже предполагается постоянный уровень инвестиций):

--1---- --1--- ΔY = ΔG ⋅ 1− mpc =6 ⋅1− 0,6 = 15 Y⋆⋆ = Y ⋆+ ΔY = 250+ 15= 265

в) Применим формулу ВВП по расходам в 2020 году без предположения о том, что ВВП стабилен:

Y = C +I + G 20 20 20 20 Y20 = (0,6Y20+ 10)+ (30+ 0,15(Y20− Y19))+ 66 Y20 = 424− 0,6Y19

Поскольку в 2019 году ВВП равнялся $Y ⋆ = 250$ , в 2020 году он станет равен:

Y20 = 424 − 0,6⋅250= 424− 150= 274

Ответ:

а) $Y ⋆ = 250$

б) $Y⋆⋆ =265$

в) $Y = 274$

Ошибка.
Попробуйте повторить позже

Задача 4#95247

В Овощной Стране есть два региона (А и В), в каждом из которых выращивают помидоры $(X)$ и огурцы $(Y )$ . В регионе А каждый житель может произвести 1 кг помидоров или 1 кг огурцов в день. В регионе В каждый житель может произвести 0,8 кг помидоров или $k ∈ (0;6]$ кг огурцов в день. Овощи потребляются только в комплектах (в порциях салата), состоящих из килограмма огурцов и килограмма помидоров. Население региона А составляет 6000 человек, а население региона В составляет 1000 человек.
a) (3 балла) Предположим, что все овощи потребляются только в тех регионах, где они произведены, распределение салата между жителями внутри региона равномерное. Какое максимальное количество порций салата (комплектов) может ежедневно получать каждый житель региона A?
б) (5 баллов) Ответьте на вопрос предыдущего пункта для жителей региона В.
в) (10 баллов) В Овощной Стране введено центральное планирование. Теперь производство осуществляется так, чтобы суммарное потребление салата в стране было максимальным. При этом комплекты будут распределяться поровну между всеми жителями обоих регионов. Сколько порций салата будет произведено в день?
г) (6 баллов) Будем говорить, что некто проигрывает, если потребление им салата уменьшается. При каких значениях параметра $k ∈ (0;6]$ жители региона А проиграют от центрального планирования?
д) (6 баллов) Ответьте на вопрос предыдущего пункта для жителей региона В.

Показать ответ и решение

$PIC$

Рис. 1 Отсутствие обменов

a) Каждый житель может произвести 0,5 кг помидоров и 0,5 кг огурцов соответственно, он и получит 0,5 порции салата. Всего в регионе будет произведено 3000 кг каждого вида овощей, то есть 6000 кг салата. Уравнение КПВ региона имеет вид: $XA + YA = 6000$ .

б) Пусть $LX$ - количество работников, занятых производством помидоров, а, $LY −$ производством огурцов. Тогда:

XB = 0,8LX; YB = kLY ; LX + LY = 1000

Уравнение КПВ региона В:

XB- + YB-= 1000 0,8 k

Приравнивая $X = Y$ , получаем:

YB = XB =--1000k-- 1,25k+ 1

Значит, каждому жителю региона достанется по $k∕(1,25k+ 1)$ кг помидоров и огурцов, то есть по $k∕(1,25k+ 1)$ порции салата (комплектов).

в) Построим суммарную КПВ. Альтернативная стоимость 1 кг помидоров в регионе А равна 1 кг огурцов. Альтернативная стоимость 1 кг помидоров в регионе В равна $1,25k$ кг огурцов. Вид общей КПВ будет зависеть от соотношения альтернативных стоимостей, то есть от того, $k ≤ 0,8$ или $k > 0,8$ .

$PIC$

Рис. 2 $k ≤ 0,8$

Случай 1. $k ≤ 0,8$ . (Случай $k = 0,8$ можно включить как в случай 1 , так в случай 2). Суммарная КПВ будет иметь вид как на рис. 2. Поскольку $6000∕800 > 1$ , луч $Y = X$ пересечет ее на нижнем участке, имеющем уравнение $Y = 6800− X$ . Значит, $6800− X =$ $X$ , откуда $X = 3400$ . Это и будет суммарное количество произведенных порций салата.

Случай 2. $k > 0,8$ . Суммарная КПВ будет иметь вид как на рис. 8.

$PIC$

Рис. 3 $k > 0,8$

Поскольку по условию $k ≤ 6$ , луч $Y = X$ пересечет ее на верхнем участке, имеющем уравнение $Y = 6000+ 1000k − X$ . Значит, $Y = 6000+ 1000k− X = X$ , откуда $X = 3000+ 500k$ .

Подытоживая, получаем, что суммарное количество произведенных порций салата равно

{ X = Y = 3400, k ≤ 0,8 3000 +500k, k ∈(0,8;6]

г) Потребление каждым жителем страны салата при центральном планировании равно (в порциях)

(| 34 -X--= -Y--= { 70, k ≤ 0,8 7000 7000 |( 6+-k, k ∈ (0,8;6] 14

Поскольку $34 < 35= 0,5 70 70$ , при $k ≤ 0,8$ жители региона А точно проиграют от планирования. При $k > 0,8$ они проиграют, если $6+ k -14--< 0,5$ , то есть $k < 1$ . Объединяя эти два случая, получаем, что жители страны А проиграют при $k ∈(0;1)$ .

д) Аналогичным образом получаем, что при $k ≤ 0,8$ жители страны В проиграют, если $34 < ---k---- 70 1,25k+ 1$ , то есть если $68< 55k$ , что невозможно при $k ≤ 0,8$ . Значит, в этом случае они точно не проиграют.

Если же $k ∈(0,8;6]$ , жители страны В проиграют, если

6+ k k -14--< 1,25k+-1-

После преобразований получаем квадратное неравенство $5k2− 22k +24 <0$ . Решением этого неравенства является область между корнями уравнения $2 5k − 22k+ 24= 0$ . Решая уравнение, получаем

√ -------- k1,2 = 11±--121-− 120 = 2; 12 5 5

Поскольку $12 = 2,4< 6 5$ , весь интервал ( $2;2,4$ ) входит в множество значений параметра, рассматриваемое в данном случае. Значит, весь интервал $(2;2,4)$ и будет ответом. Жители страны Б проиграют при $k ∈ (2;2,4)$ .

Ответ:

а) 6000

б) $---k---- 1,25k + 1$

в) ${ 3400 k ≤ 0,8 3000 +500k k ∈ (0,8;6]$

г) $k ∈ (0;1)$

д) $k ∈(2;2,4)$

Ошибка.
Попробуйте повторить позже

Задача 5#95250

Рынок медицинских масок в стране Z совершенно конкурентный. Функция издержек фирмы, если она вошла на рынок, задается уравнением $T C(q) =q2 +4$ , где $q−$ количество масок, произведенное данной фирмой (в тыс. шт.). Если фирма не входит на рынок, ее прибыль равна нулю. В краткосрочном равновесии число фирм на рынке фиксировано. В долгосрочном равновесии число фирм определяется таким образом, что каждой фирме безразлично, входить на рынок или нет.
a) (14 баллов) Изначально рыночный спрос на маски задавался уравнением $Q0(P) =$ $= 40− P$ и рынок находился в состоянии долгосрочного равновесия. Найдите рыночные цену, объем и количество фирм в этом равновесии.
б) (6 баллов) В связи с пандемией спрос на маски резко вырос - до $Q1(P)= 400− P$ . Однако в краткосрочном периоде новые фирмы не успели войти на рынок, чтобы удовлетворить возросший спрос, и число фирм осталось таким же, как в пункте а). Найдите рыночные цену и объем в новом краткосрочном равновесии.
в) (10 баллов) С течением времени спрос остался на уровне $Q1(P) = 400 − P$ , однако на рынок вошли новые фирмы, желающие заработать. Установилось новое долгосрочное равновесие. Найдите рыночные цену, объем и количество фирм в этом равновесии.

Показать ответ и решение

a) Способ 1. Типичная фирма максимизирует прибыль

π(q) =P q− q2− 4→ max q≥0

Графиком этой квадратичной функции является парабола с ветвями вниз и вершиной в точке $q⋆(P)= 0,5P$ (это не что иное, как функция предложения каждой вошедшей на рынок фирмы). Заметим, что при оптимальном поведении фирмы её прибыль обращается в ноль при цене $P = 4$ :

2 2 maxπ(q)= π(0,5P)= P ⋅0,5P − (0,5P) − 4= 0,25P − 4 =0.

Значит, именно такая цена сложится в долгосрочном равновесии. Потребители захотят купить по этой цене $Q0(4)= 36$ единиц продукции, тогда как каждая действующая на рынке фирма произведёт по $q⋆(4)= 2$ единицы; значит, на рынок войдёт $Q0(4)∕q⋆ = 18$ фирм.

Способ 2. Вспомним, что долгосрочное равновесие на совершенно конкурентном рынке определяется условием $P = MC = AC$ ; заметим, что $MC$ возрастают, поэтому данное условие может быть применено.

Имеем $′ MC =T C (q)= 2q,AC = TC∕q =q +4∕q$ . Из условия $MC = AC$ получаем $⋆ 2q =q +4∕q,q = 2$ , значит $⋆ P = MC =2q = 4$ . Потребители по этой цене захотят купить $Q (4)= 36 0$ единиц продукции; значит, на рынок войдёт $Q0(4)∕q⋆ = 18$ фирм.

Способ 3 отличается от способа 2 лишь тем, как получается $q⋆ = 2$ . А именно, $q⋆ = 2$ можно найти из задачи минимизации средних издержек, $AC = q +4∕q → min$ , $AC ′ =1 − 4∕q2 = 0$ , производная меняет знак с минуса на плюс, $q⋆ = 2$ . Тот же ответ можно получить из неравенства о средних.

б) В пункте а) было установлено, что функция предложения каждой фирмы имеет вид $⋆ q = 0,5P$ ; рыночное предложение составит $⋆ QS =18q = 9P$ . Тогда в новом краткосрочном равновесии $Q1(P)= QS (P )$ , или $400− P = 9P$ , откуда $P = 40Q =360$ .

в) В пункте а) получено, что в долгосрочном равновесии $P =4$ , вывод это цены не зависит от функции спроса. Потребители по этой цене захотят купить $Q1(4)= 396$ единиц продукции, каждая фирма произведёт по $q⋆(4)= 2$ единицы; значит, на рынке будет $Q1∕q⋆ = 198$ фирм.

Ответ:

а) $P = 4,Q = 36,N = 18$

б) $P = 40,Q = 360$

в) $P = 4,Q = 396,N = 198$

Ошибка.
Попробуйте повторить позже

Задача 6#95253

Фирма-монополист работает на рынке со спросом $qd = 15− p$ , а производство каждой единицы продукции обходится фирме в 5 д.е. Фирма облагается налогом на прибыль по ставке $20%$ (естественно, только в случае, если прибыль положительна), но у фирмы есть возможность задекларировать вместо фактической прибыли какуюто меньшую величину и тем самым уклониться от налога. Однако уклонение не является бесплатным: чтобы не платить налог с $x$ д.е. прибыли, необходимо понести затраты в размере $2 0,01x$ д.е. Оплата услуг по уклонению от налога «неофициальна»: фирма не отражает сумму $0,01x2$ в своих издержках, оплачивая её неформально из своей чистой прибыли, т.е. после уплаты налога.
a) (6 баллов) Какую чистую прибыль получит фирма, если она не будет уклоняться от уплаты налога?
б) (12 баллов) Какую настоящую чистую прибыль (с учётом издержек на уклонение) получит фирма в случае уклонения от налога? Фирма выбирает уровень уклонения $x$ оптимальным образом.
в) (12 баллов) Предположим, государство заинтересовано собрать как можно больше налогов (зная об уклонении, но не имея возможности с ним бороться). После того как государство выбирает ставку налога, фирма выбирает выпуск и уровень уклонения от налога. Какую ставку налога на прибыль следует установить государству?

Показать ответ и решение

a) Фирма максимизирует чистую прибыль:

πnet(q) =(1− t)π0(q)= (1− 0,2)((15− q)q − 5q)= 0,8 (10q− q2)→ max q≥0

Функция прибыли является квадратичной, ветви параболы направлены вниз, вершина в точке $q⋆ = 5$ ; прибыль до вычета налога составит $π0 = 25$ ; чистая прибыль (после вычета налога) составит $πnet =20$ .

б) Фирма заработает прибыль $π0(q)$ , затем задекларирует прибыль на уровне $π0(q)− x$ , после чего заплатит с этой величины налог, равный $t(π0(q)− x)$ , и ещё неофициальным образом оплатит услуги по уходу от налога $0,01x2$ . Таким образом, целевая функция фирмы примет вид

( ) πnet(q,x)= π0(q)− t(π0(q)− x)− 0,01x2 = (1− t)π0(q)+tx−0,01x2 = 0,8 10q− q2+0,2x−0,01x2

Можно увидеть, что чистая прибыль является суммой двух независимых квадратичных функций, ветви парабол направлены вниз, вершины в точках $⋆ q = 5$ (выпуск по сравнению с пунктом а) не меняется) и $⋆ x = 10$ . «Настоящая» чистая прибыль фирмы составит $πnet = 21$ .

в) Аналогично пункту б), целевая функция фирмы имеет вид

2 ( 2) 2 πnet(q,x)= (1 − t)π0(q)+ tx− 0,01x = (1− t) 10q− q +tx − 0,01x

Можно увидеть, что чистая прибыль является суммой двух независимых квадратных парабол с ветвями вниз и вершинами в точках $q⋆ = 5$ (выпуск по сравнению с пунктом а) не меняется) и $x⋆ = 50t$ . (Строго говоря, $x⋆ =min {50t;π0(q⋆)}$ .)

Налоговые поступления (доля $t$ от декларируемой прибыли), если они больше нуля, составят

T(t)= t(π (q)− x) =t(π (5)− x⋆(t))= t(25 − 50t) 0 0

Государство максимизирует эту функцию по $t∈ [0;1]$ . Функция $T(t)$ квадратичная, ветви параболы направлены вниз, вершина в точке $t⋆ = 0,25$ .

Ответ:

а) $πnet = 20$

б) $πnet = 21$

в) $t⋆ = 25%$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#95257

В закрытой экономике потребители расходуют две трети от своего располагаемого дохода и вдобавок - при любом значении располагаемого дохода - еще 10 д.е., составляющих автономное потребление. Инвестиции постоянны и равны 40 д.е. В стране взимаются только подоходные налоги по ставке $25%$ ; аккордных налогов и трансфертных платежей нет. Известно также, что потенциальный ВВП этой экономики составляет 300 д.е. Правительство, реализуя свою фискальную политику, может воздействовать только на государственные закупки.
a) (20 баллов) На каком уровне следует установить госзакупки (без изменения текущей ставки подоходного налога), чтобы в экономике установился потенциальный ВВП? А чтобы в экономике был сбалансированный госбюджет?
б) (10 баллов) Теперь предположим, что правительство преследует две цели одновременно и выбирает некий компромиссный вариант. Вторая цель для правительства в 4 раза более важна, чем первая, и потому потери правительства от несоответствия выпуска своему потенциальному значению и от несбалансированного бюджета определяются как

L = (Y − Y ⋆)2+ 4⋅s2

где $Y$ - фактический ВВП, $⋆ Y$ - потенциальный ВВП, $s$ - сальдо госбюджета. Чему будут равны госзакупки, если правительство будет принимать решение, минимизируя свои потери?

Показать ответ и решение

a) Поскольку экономика закрытая, $Ex = Im = Xn = 0$ , и ВВП будет равен $Y =$ $= C + I + G$ . По условию $C = CA+ mpc ⋅Yd = 10+ (2∕3)⋅Yd$ . В силу отсутствия аккордных налогов и трансфертов $T =tY = 0,25Y$ и $Yd = Y − T = 0,75Y$ . Учтя, что $I = 40$ , составим уравнение

Y =10 +(2∕3)⋅0,75Y +40 +G

Выразив выпуск, получим $Y = 100 +2G$ . Для достижения потенциального ВВП, или формально $⋆ Y1 =Y$ , должно выполняться $100 +2G1 = 300$ , откуда $G1 = 100$ . Сальдо бюджета определяется как разница между доходами бюджета и расходами бюджета:

s= tY − G = 0,25(100+ 2G)− G = 25− 0,5G

Чтобы бюджет был сбалансирован, сальдо должно равняться нулю: $25− 0,5G = 0 2$ , откуда $G = 50 2$ .

б) Подставим в задачу правительства найденные ранее $Y = 100+ 2G$ и $s =25 − 0,5G$ :

L(G)= (Y(G)− Y⋆)2+s2(G )= (100+2G −300)2+4 (25−0,5G)2 = 5(G2− 180G +8500)→ min G ≥0

Целевая функция является квадратичной, ветви параболы направлены вверх, минимум достигается в вершине: $G⋆ = 90$ .

Ответ:

а) $G1 = 100,G2 = 50$

б) $G⋆ = 90$

Ошибка.
Попробуйте повторить позже

Задача 8#95261

На острове Паабалор есть два племени, живущие охотой и собирательством. Племена потребляют мясо $(x)$ и плоды $(y)$ ) Уравнения и графики КПВ имеют вид:

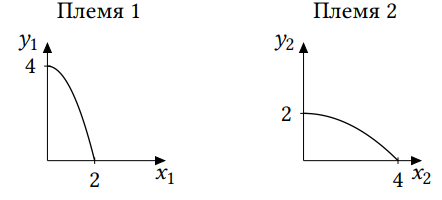
a) (8 баллов) Какое максимальное количество плодов может быть собрано на острове, если всего нужно добыть 3 единицы мяса?
б) (8 баллов) Какое максимальное количество плодов может быть собрано на острове, если всего нужно добыть 5 единиц мяса?
в) (14 баллов) Определите уравнение КПВ острова.

Показать ответ и решение

a) Найдем, как нужно разделить обязанности племен по добыче 3 единиц мяса, чтобы в итоге количество собранных плодов было максимально, то есть решим задачу

y1+ y2 = 6− x21− x22∕8 → max

при условии $x1 +x2 =3$ , а также $x1 ∈ [0;2],x2 ∈ [0;4]$ . Подставляя в целевую функцию $x2 = 3− x1$ , получаем задачу

6− x21− (3− x1)2∕8 → max

При этом найти максимум этой функции надо на отрезке [0;2], так как первое племя не может добыть больше 2 единиц мяса. При этом производство второго племени будет изменяться от 1 до 3 . Эти количества для второго племени возможны, так что дополнительных ограничений не возникает. Находя вершину этой параболы с ветвями вниз, получаем, что $x⋆= 1∕3 1$ , что принадлежит отрезку [0;2]. Значит, это и есть искомый максимум. Второе племя будет производить $3 − 1∕3= 8∕3$ единиц мяса. Общее количество собранных плодов при этом равно $6 − (1∕3)2− (8∕3)2∕8= 5$ .

Тот же ответ можно получить, если оптимизировать по $x2$ функцию $6 − (3− x2)2 −$ $− x22∕8$ . Оптимизировать нужно на отрезке $[1;3]$ , так как $x2 ≤3$ в силу ограничения на общее количество мяса и $x1 ≥ 0$ , и $x2 ≥1$ в силу ограничения на общее количество мяса и $x1 ≤2$ .

Кроме того, точку $⋆ x1 = 1∕3$ можно получить, приравнивая производную целевой функции к нулю, или, что эквивалентно, приравнивая альтернативные издержки производства для двух племен. Для первого племени альтернативные издержки равны $||( 2)′|| |4− x1 |= 2x1$ , для второго $||( 2 )′|| −| 2− x2∕8 |= x2∕4$ .

б) Теперь нужно решить задачу

y1+ y2 = 6− x21− x22∕8 → max

при условиях $x1 +x2 =5,x1 ∈ [0;2],x2 ∈[0;4]$ . Аналогично пункту а), получаем задачу

6− x21− (5− x1)2∕8 → max

Второе племя не может добыть больше 4 единиц мяса. Значит, первому племени надо будет добыть минимум одну единицу мяса. Таким образом, максимум этой функции мы будем искать на отрезке [1;2]. Вершиной данной параболы с ветвями вниз является точка $x = 5∕9< 1 1$ , и значит, максимум будет достигаться на краю отрезка, в точке $x⋆= 1 1$ . Второе племя произведет все оставшиеся четыре единицы, а количество собранных плодов будет равно 3.

Тот же ответ можно получить, если оптимизировать по $x2$ функцию 6 - $(5 − x2)2$ $− x22∕8$ . Оптимизировать нужно на отрезке $[3;4];x2 ≥ 3$ в силу ограничения на общее количество мяса и $x1 ≤2$ .

Кроме того, решение $x⋆1 = 1$ можно получить, если заметить, что производная целевой функции $2 2 6− x1− (5− x1) ∕8$ отрицательна на отрезке [1;2], или, что эквивалентно, для любого $x1 ∈ [1;2]$ альтернативные издержки добычи мяса первым племенем в точке $x1$ больше, чем альтернативные издержки добычи мяса вторым племенем в точке $5− x1$ .

в) КПВ есть не что иное, как график функции, показывающей, какое максимальное количество Игрека можно произвести, если всего требуется произвести $X$ единиц Икса. Две точки на КПВ острова мы уже нашли - (3;5) и (5;3). Теперь осталось найти остальные, решив ту же задачу максимизации уже для произвольного значения $X$ , то есть

Y = y1+ y2 = 6− x21− x22∕8 → max

при условиях $x1+ x2 =X, x1 ∈ [0;2],x2 ∈ [0;4]$ . Ясно, что $X ∈ [0;6]$ . Переходя к оптимизации по одной переменной, получаем задачу

2 2 6− x1− (X − x1) ∕8→ max

где $X$ - параметр. Если $X ≤ 4$ , эту задачу надо решать на отрезке $[0;2]$ - для любого $x1 ∈ [0;2]$ , второе племя сможет произвести $X − x1$ . Если же $X > 4,x1 ∈ [X − 4;2]$ , так как первое племя должно будет произвести минимум $X − 4$ единицы мяса.

Нетрудно определить, что вершина параболы с ветвями вниз $6− x21− (X − x1)2∕8$ находится в тотiле $x1− X∕9$ .

Случай 1. $X ≤4$ , и поэтому $x1 ∈ [0;2].X ∕9$ принадлежит этому отрезку для любого $X ≤ 4$ , а значит, $⋆ x1(X )= X∕9$ будет решением задачи. Тогда $2 2 Y = 6− (X∕9) − (8X ∕9) ∕8=$ $2 = 6− X ∕9$ .

Случай 2. $X ∈(4;6]$ , и поэтому $x1 ∈ [X − 4;2]$ . $X ∕9$ принадлежит этому отрезку при $X∕9≥ X − 4$ , или $X ≤4,5$ . Значит, решением будет

{ x⋆(X) = X∕9, X ≤ 4,5 1 X − 4, X > 4,5

Действительно, если вершина параболы с ветвями вниз лежит левее допустимого отрезка, оптимум достигается в левом конце отрезка. При $X > 4,5$ максимальное количество собранных плодов будет равно

Y = 4− (X − 4)2+ 0= 4− (X − 4)2

Обобщая, получаем, что КПВ острова задается уравнением

{ 6− X2∕9, X ≤ 4,5 Y = 4− (X − 4)2, 4,5 ≤ X ≤6

Тот же ответ можно получить, оптимизируя по $x2$ и обобщая анализ в пунктах а) и б). При $X < 2$ максимизацию по $x2$ нужно проводить на отрезке [0;4], а при $X ≥ 2−$ на отрезке $[X − 2;4]$ . Граничное значение $X = 4,5$ определяется из условия $8X ∕9 = 4$ .

Кроме того, решить пункт можно с помощью производной или анализа альтернативных издержек. При $X ≤ 4,5$ является доступным распределение $(x1,x2)=$ $(X∕9,8X ∕9)$ , при котором производная целевой функции равна нулю (альтернативные издержки двух племен равны). Поскольку альтернативные издержки обоих племен возрастают, производная целевой функции убывает, и значит, это точка максимума. При $X > 4$ это распределение не является доступным, так как $8X∕9> 4$ . При оптимизации по $x1$ производная целевой функции отрицательна на отрезке $[X − 4;2]$ альтернативные издержки первого племени больше в точке $x1$ , чем альтернативные издержки второго племени в точке $X − x1$ - и потому оптимальным является минимальное значение $x1$ , то есть $X − 4$ .

Ответ:

а) 5

б) 3

в) ${ 6 − X2 ∕9, X ≤ 4,5 Y = 4 − (X − 4)2, 4,5≤ X ≤ 6$

Ошибка.
Попробуйте повторить позже

Задача 9#95269

Юрист Савва зарабатывает $w$ рублей в час (за полчаса $w∕2$ рублей, за 10 минут $w ∕6$ рублей и т. д.). Савва должен решить, как ему организовать свое питание. Есть три варианта:

1.: ходить в магазин за продуктами и готовить еду самому;
2.: заказывать в интернете продукты с доставкой и готовить еду самому;
3.: заказывать в интернете готовую еду с доставкой.

Стоимость продуктов на один прием пищи как в магазине, так и в интернете (без учета доставки) составляет 600 руб. Стоимость готовой еды при ее заказе в интернете составляет 1200 руб. без учета доставки. Стоимость доставки продуктов или доставки готовой еды составляет 500 руб. Поскольку Савва употребляет только свежие продукты и только что приготовленную еду, он ходит в магазин или заказывает доставку перед каждым приемом пищи. Поход в магазин занимает 30 минут. Готовка еды занимает 45 минут. Временем на сам прием пищи можно пренебречь.

Савва минимизирует экономические издержки, связанные с организацией своего питания. У Саввы есть сбережения, так что ему хватит денег на любой из вариантов при любом $w$ . Для каждого $w ≥ 0$ определите, какой из трех вариантов оптимален для Саввы (если оптимальных вариантов несколько, укажите все).

Показать ответ и решение

Рассчитаем экономические издержки для каждого из трех вариантов.

1: $C1(w)= 600+ w∕2+ 3w∕4= 600+ 5w∕4$ . (Второе и третье слагаемые есть альтернативные издержки времени, потраченного на поход в магазин и готовку соответственно.)

2: $C2(w)= 600+ 500+ 3w ∕4= 1100+ 3w ∕4$ . (Второе слагаемое есть альтернативные издержки времени, потраченного на готовку.)

3: $C3(w)= 1200+ 500 = 1700$

1) Сначала определим, при каких $w$ второй вариант лучше первого. Это так тогда и только тогда, когда $C2(w) <C1(w)$ , то есть $1100 +3w∕4 < 600 +5w ∕4$ , $w ∕2 > 500,w > 1000$ . Соответственно, при $w <1000$ первый вариант лучше второго, при $w = 1000$ издержки одинаковы.

Сравнить варианть 1 и 2 можно и без подсчета всех экономических издержек. Поскольку в обоих вариантах 1, 2 Савва готовит, вариант 2 выгоднее, если стоимость доставки продуктов меньше, чем альтернативные издержки времени, затраченного на поход в магазин, то есть $500< w∕2$ , $w > 1000$ .

2) Теперь определим, при каких $w$ третий вариант лучше второго. Это так тогда и только тогда, когда $C3(w) <C2(w)$ , то есть $1700 <1100+ 3w∕4$ , то есть $w > 800$ . Соответственно, при $w < 800$ второй лучше третьего, при $w = 800$ издержки одинаковы.

Сравнить варианты 2 и 3 можно и без подсчета всех экономических издержек. Поскольку в обоих вариантах 2, 3 Савва платит за доставку, вариант 3 выгоднее, если разница стоимости готовой еды и стоимости продуктов меньше, чем альтернативные

издержки времени, потраченного на готовку, то есть 1200 - $600< 3w ∕4,w > 800$ . 3) Из сравнений выше следует, что второй вариант не оптимален ни при каком $w ≥0$ . Действительно, при $w <1000$ он хуже первого, а при $w > 800$ он хуже третьего. Но для любого $w ≥ 0$ хотя бы одно из двух неравенств $w < 1000,w > 800$ обязательно выполнено. 4) Значит, оптимален либо первый, либо третий вариант. Сравним их. $C1(w)<$ $C3(w)$ при $600+ 5w∕4 <1700,5w ∕4< 1100,w < 880$ . Значит, первый вариант оптимален при $w < 880$ , третий при $w > 880$ , при $w = 880$ они оба оптимальны.

Ответ:

При $w < 880$ - вариант 1;

При $w =880$ - варианты 1 и 3;

При $w >880$ - вариант 3.

Ошибка.
Попробуйте повторить позже

Задача 10#95270

В стране Z совокупный спрос описывается уравнением $Y = 250− 100P − 10r$ , где $Y −$ реальный ВВП, $P$ - уровень цен, $r$ - ключевая ставка центрального банка в процентах. Например, если ключевая ставка равна $4%$ , то уравнением совокупного спроса будет $Y = 250− 100P − 10⋅4 = 210 − 100P$ .

В 2120 году краткосрочное совокупное предложение описывалось уравнением $Y = 100P$ ; экономика страны Z находилась в состоянии в состоянии краткосрочного и долгосрочного равновесия. Ключевая ставка была равна $5%$ . В 2121 году началась очередная пандемия, и из-за нарушения цепочек поставок краткосрочное совокупное предложение сократилось до $Y = 100P − 50$ . Потенциальный ВВП не изменился. В 2121 году равновесие в экономике только краткосрочное, оно устанавливается один раз и с учетом действий ЦБ.
a) (7 баллов) Определите годовой темп инфляции в 2121 году, если центральный банк не изменит ключевую ставку.
б) (5 баллов) Предположим, что ЦБ придерживается политики таргетирования инфляции на уровне $5%$ в год. Какую ключевую ставку установит ЦБ в 2121 году, чтобы удержать годовую инфляцию на уровне $5%$ ?
в) (18 баллов) Теперь предположим, что ЦБ заботится не только об инфляции, но и о реальном ВВП. ЦБ выбирает ключевую ставку так, чтобы минимизировать потери в 2021 году от несоответствия инфляции целевому уровню $π⋆ = 5$ , а ВВП - своему потенциальному уровню $Y ⋆ :L = 8(π − 5)2+ (Y − Y ⋆)2$ , где $L −$ потери, $π$ - годовой темп инфляции в 2121 году в процентах. Определите оптимальную ключевую ставку и годовой темп инфляции в 2121 году.

Показать ответ и решение

a) Найдем сначала равновесный уровень цен в 2120 году. Поскольку $r =5$ , имеем $250− 100P − 10⋅5 =100P,200= 200P,P =1$ .

Теперь найдем равновесный уровень цен в 2121 году при $r = 5.250− 100P−$ $50 =100P − 50,250= 200P,P = 5∕4= 1,25$ . Значит, годовая инфляция составит $1,25− 1 π = --1-100% = 25%$ .

б) Ставка $r$ должна быть выбрана так, чтобы равновесный уровень цен составил 1,05 . Значит, $Y = 250 − 100 ⋅1,05− 10r = 100 ⋅1,05− 50,300− 200⋅1,05= 10r,90 = 10r,r = 9$ , ставку нужно повысить до $9%$ .

в) Сначала определим значение потенциального ВВП. Поскольку в 2120 году имело место не только краткосрочное, но и долгосрочное равновесие, потенциальный ВВП $Y⋆$ равен равновесному ВВП в 2120 году, то есть $Y ⋆ = Y = 100P = 100⋅1= 100$ .

Далее можно двигаться двумя способами.

Способ 1. Найдем краткосрочное равновесие при каждом $r.250− 100P − 10r = 100P−$ 50, откуда

P = 300−-10r 200 Y =100300−-10r− 50= 100− 5r 200

От уровня цен перейдем к инфляции в процентах:

300-− 10r π = 100(P − 1)= 100 200 − 100= 50− 5r

Подставляя выражения для выпуска и инфляции, а также значение потенциального выпуска $Y⋆ =100$ в функцию потерь, получаем

( ) L(r) = 8(50− 5r− 5)2+(100− 5r− 100)2 = 8(45− 5r)2+(5r)2 =25 8(9− r)2 +r2 .

Центробанк минимизирует функцию $L (r)$ . Приравняем производную к нулю:

L′(r)= 50(− 8(9 − r)+ r)= 0 −72 +9r =0 r = 8

$L′(r)$ возрастает (меняет знак с минуса на плюс), а значит, найденная точка является точкой минимума.

Также можно заметить, что функция потерь квадратичная, ветви параболы направлены вверх, поэтому минимум будет достигаться в вершине параболы, которая также находится в точке $r =8$ .

Наконец, найдем уровень инфляции при $r = 8:π =50 − 5 ⋅8 = 10$ .

Способ 2. Сначала найдем, какой темп инфляции (или уровень или уровень выпуска) оптимален для ЦБ (с учетом его заботы о ВВП), и затем определим, какая ставка $r$ реализует данный темп инфляции (или уровень цен или уровень выпуска). 1) Независимо от действий ЦБ выполнено уравнение предложения $Y = 100P − 50$ , которое в терминах инфляции можно переписать как $Y = 100(1 +π∕100)− 50= 50+ π$ . Значит, мы можем получить выражение для потерь в зависимости от инфляции $π$ :

L(π)= 8(π− 5)2 +(50+ π − 100)2 = 8(π − 5)2+ (π− 50)2

Минимизируя эту функцию, получаем $L′(π)= 2(8π− 40+ π− 50)= 0$ , откуда $π = 10.L′(π)$ возрастает (меняет знак с минуса на плюс), а значит, найденная точка является точкой минимума. Также можно заметить, что функция потерь квадратичная, ветви параболы направлены вверх, поэтому минимум будет достигаться в вершине параболы, которая также находится в точке $π = 10$ .

Ответ:

а) $25%$

б) $9%$

в) Оптимальная ключевая ставка составит $8%$ , темп инфляции - $10%$

Ошибка.
Попробуйте повторить позже

Задача 11#95271

В стране есть три региона, КПВ которых описываются уравнениями $y1 = 10 − x1$ , $y2 = 2(10− x2),y3 = 3(10 − x3)$ . Изначально страна открыта для свободной торговли. На мировом рынке валютой является тугрик. На мировом рынке можно купить или продать любые количества товаров по ценам $px = 30$ тугриков (цена товара икс), $py =$ $= 20$ тугриков (цена товара игрек). До торговли у страны нет тугриков.

Во всех пунктах задачи укажите на рисунках координаты точек пересечения КПВ (КТВ) с осями и координаты точек излома КПВ (КТВ).
a) (6 баллов) Постройте КПВ страны.
б) (8 баллов) Постройте кривую торговых возможностей (КТВ) страны на том же рисунке, что и в а). (КТВ является верхней границей множества наборов ( $X, Y$ ), доступных для потребления страной после производства и торговли.)
в) (16 баллов) Против страны введена торговая санкция по следующему правилу: внешнеторговый оборот страны (сумма стоимости импорта и экспорта) не может превышать 960 тугриков. Постройте новую КТВ страны на новом рисунке.

Показать ответ и решение

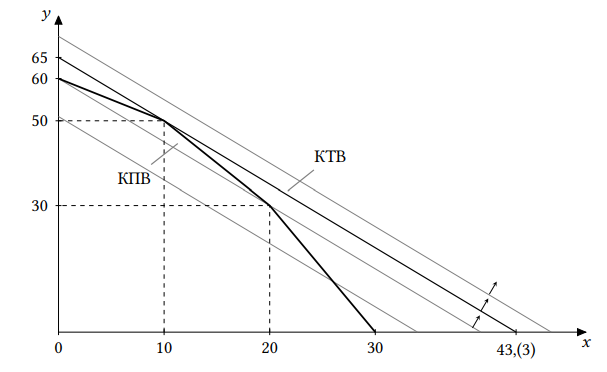
a) Складывая КПВ регионов стандартным образом, получаем, что КПВ страны есть ломаная, соединяющая точки $(0;60),(10;50),(20;30)$ и $(30;0)$ . КПВ имеет следующий вид:

$PIC$

Рис. 1 КПВ страны. КТВ в пункте б)

б) Способ 1 (через сравнение А.И. и пропорции обмена). Пропорция обмена на мировом рынке равна $20:30= 1:1,5$ , одну единицу товара икс можно купить за 1,5 единицы товара игрек. Для максимизации потребления товара игрек при данном количестве товара икс нужно производить икс только в тех регионах, где альтернативные издержки его производства меньше, чем его цена (в единицах игрека) на мировом рынке. Альтернативные издержки производства товара икс в каждом регионе равны номеру региона. Поскольку $1< 1,5< 2 < 3$ , производить товар икс нужно только в первом регионе.

Таким образом, страна будет производить $X = 10$ единиц товара икс и $Y = 20+$ $30= 50$ единиц товара игрек. Стартуя в этой точке, страна сможет обменивать икс на игрек в пропорции $1:1,5$ . Значит, КТВ является отрезком прямой с наклоном $(− 1,5)$ , проходящей через точку ( $10;50$ ). Несложно установить, что эта прямая пересекает ось икс при $x = 43+ 1∕3$ , ось игрек при $y = 65$ . (Ее уравнение $Y = 65− 1,5X$ или $3X + 2Y = 130$ .)

Способ 2 (геометрический). Геометрически международная торговля представляет собой движение вдоль некой прямой $l$ . Эта прямая имеет наклон, соответствующий пропорции обмена, в нашем случае $− px∕py = −1,5$ , и проходит через точку $(X0,Y0)$ , соответствующую объемам производства (точка ( $X0,Y0$ ) должна лежать на или под КПВ.) КТВ будет соответствовать той из этих прямых, что лежит выше других. Проводя разные такие прямые одном на рисунке с КПВ (они изображены на рис. 7.1 светло-серым цветом), видим, что выше других лежит прямая, проходящая через точку (10;50). Это и есть искомая КТВ. Зная ее наклон, находим точки пересечения с осями.

Способ 3 (через максимизацию выручки). Этот способ близок к способу 2. Представим себе, что вместо того, чтобы продавать один товар и покупать другой, потребляя в итоге набор $(X1,Y1)$ , страна сначала продает на мировом рынке все произведенные единицы обоих товаров, а затем на полученные тугрики покупает потребительский набор $(X1,Y1)$ . Те единицы, которые не торговались на мировом рынке в первом случае, во втором случае страна продает и покупает назад. Поскольку цены для покупки и продажи одинаковы, с помощью второй процедуры можно получить ровно те же наборы, что просто в результате торговли. Но во втором случае потребление товаров будет максимально (например, максимально потребление товара игрек при данном количестве товара икс), если «потребительский бюджет» страны будет максимален. А он равен выручке. Это рассуждение приведено здесь для полноты. От участника олимпиады это рассуждение не требуется, участник может максимизировать выручку без обоснования.

Выручка страны в тугриках равна $30X + 20Y$ . Максимизируя ее графическим способом (проводя разные кривые одинаковой выручки $30X + 20Y =$ const, на рис. 7.1 они светло-серые), получаем, что максимальная выручка достигается, если производить $X = 10$ единиц товара икс и $Y = 20+ 30= 50$ единиц товара игрек. Выручка будет равна $30⋅10 +20⋅50 =1300$ Линия максимальной выручки $30X + 20Y = 1300(3X + 2Y = 130)$ и будет искомой КТВ. Из уравнения находим точки пересечения с осями.

Кроме того, выручку можно максимизировать и аналитически, подставляя в функцию выручки $30X +20Y$ аналитическое выражение для КПВ $Y (X )$ и максимизируя выражение $30X +20Y (X )$ по $X$ . в) Поскольку для максимизации потребления стоимость импорта должна быть равна стоимости экспорта (если бы стоимость экспорта была больше, было бы лучше часть товаров не экспортировать, а потреблять), данная санкция эквивалентна тому, что стоимость импорта не может превышать $960∕2 =480$ тугриков и стоимость экспорта не может превышать $960∕2 = 480$ тугриков.

Следовательно, импорт и экспорт товара икс не может превышать $480∕30= 16$ единиц, импорт и экспорт товара игрек не может превышать $480∕20 =24$ единицы, причем достаточно рассмотреть только ограничения по товару икс, ограничения по товару игрек автоматически следуют из того, что стоимости экспорта и импорта равHы.

При производстве $X = 10$ единиц страна сможет экспортировать не больше $10 <16$ единиц товара икс, так что ограничение повлияет на КТВ страны только при импорте товара икс. Значит, отрезок $(0;65)− (10;50)$ старой КТВ принадлежит и новой КТВ.

Стартуя в точке $(10;50)$ , страна сможет сдвинуться вправо вдоль старой КТВ (полученной в пункте б) только на расстояние 16 по оси икс. При $X = 10+ 16= 26$ объем потребления товара игрек равен $50− 24= 26$ . Отрезок $(10;50)− (26;26)$ будет принадлежать новой КТВ.

При $X > 26$ страна уже не сможет обеспечить объемы потребления товара игрек, как в б). Чтобы потреблять более 26 единиц товара икс, стране придется увеличивать производство товара икс. При этом, поскольку альтернативные издержки производства икс будут больше 1,5 , оптимальным является использование возможностей торговли по максимуму, то есть страна будет импортировать 16 единиц товара икс и экспортировать 24 единицы товара игрек. Значит, КТВ при $X > 26$ будет получаться путем сдвига части КПВ правее точки $(10;50)$ на вектор $(16;− 24)$ .

Таким образом, новая КТВ будет иметь вид:

$PIC$

Рис. 2 КТВ в пункте в)

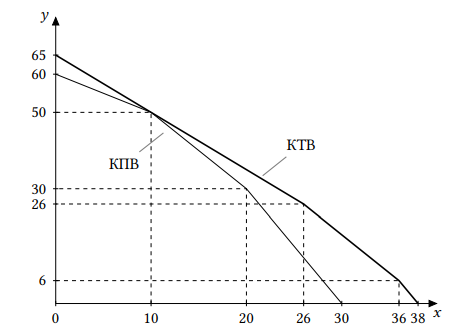
Это ломаная линия, соединяющая точки $(0;65),(26;26),(36;6)$ и $(38;0)$ . (Координата 38 получена так: последний участок КТВ имеет наклон 3 и проходит через точку ( $36;6$ ), значит он пересекает ось $x$ при $X = 36 +6∕3 =38$ .) г) Поскольку при оптимальном поведении страна тратит всю валютную выручку от экспорта на импорт, стоимость импорта равна стоимости экспорта, и две санкции абсолютно эквивалентны. КТВ будет такой же, как и в пункте в), ответ не изменится.

Ответ:

Требуемые графики предоставлены в решении

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#95272

Функция спроса на продукцию монополиста описывается уравнением $Q = 10$ - $P$ , а средние издержки постоянны и равны 2 . Государство вводит потолок цены в размере $x$ . Ограничение цены, однако, не является жестким. Если фирма нарушает условие о потолке цены, то она должна заплатить штраф в размере 9, при этом переустанавливать цену не нужно. Если фирма безразлична между несколькими разными ценами, она назначает меньшую из них.

Для каждого $x ≥ 0$ найдите цену $⋆ P (x)$ , которую установит фирма. Постройте график функции $P⋆(x)$ .

Показать ответ и решение

Сначала найдем, какую цену устанавливала бы фирма в отсутствие ограничения цены. Прибыль монополиста равна $π(P) = (10− P)(P − 2)$ , это парабола с ветвями вниз и вершиной в точке $P = 6$ , при этом объем выпуска равен $Q = 4$ , а значение прибыли равно 16. Такой же результат можно получить, приравнивая $MR = 10− 2Q$ и $MC = 2$ или максимизируя функцию прибыли от $Q :π(Q)= (10− Q)Q − 2Q$ .

Если фирма установит оптимальную для себя цену и заплатит штраф, то ее прибыль будет равна $16− 9= 7$ . Если следование ограничению цены приводит к меньшей прибыли, то выгоднее платить штраф.

Рассчитаем оптимальную цену и прибыль фирмы, если фирма подчиняется потолку цены $x$ .

Случай 1: $x≥ 6$ . Если потолок цены не заставляет фирму снижать цену, то для фирмы ничего не поменяется она установит цену $P ⋆ = 6$ . Прибыль при этом будет равна 16 .

Случай 2: $2≤ x< 6$ . В этом случае фирме придется снижать цену (или платить штраф), но, подчинившись, она всё еще может получать неотрицательную прибыль. Эта прибыль будет равна $(10− x)(x− 2)$ .

Случай 3: $x< 2$ . В этом случае фирме невыгодно работать на рынке, так как цена ниже ее средних издержек.

Очевидно, что в случае 1 фирма не будет платить штраф (потому что ее оптимальная цена ничего не нарушает), а в случае 3 - будет (потому что иначе прибыль отрицательная). Что касается случая 2 , то решение фирмы зависит от $x$ : если он достаточно низок, чтобы прибыль фирмы с ним была меньше 1200 , то выгоднее заплатить штраф, иначе нужно следовать ограничению. Найдем значения $x$ , при которых штраф выгоднее:

(10 − x)(x− 2)< 7 x< 3 или x > 9

Интервал $x > 9$ не подходит, потому что тогда потолок ничего не ограничивает (случай 1). Получается, что при потолке ниже 3 (в том числе ниже 2) фирма будет платить штраф и устанавливать цену 6 , при потолке от 3 до 6 она будет следовать ограничению, а при потолке от 6 и выше будет просто вести себя как обычно. Запишем функцию $⋆ P (x)$ аналитически и построим график:

Ответ:

$( |{ 6, если x <3; P ⋆(x)= x, если 3 ≤x < 6 |( 6, если x ≥6.$

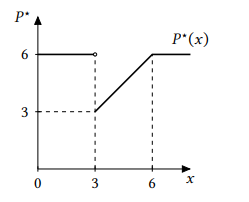
Ошибка.
Попробуйте повторить позже

Задача 13#95277

Фирма «ЭПВВв» производит параболические антенны. Производственная функция фирмы имеет вид

{ } {L2, L2 ≤ K Q(L,K )= min L2,K = K, L2 > K

где $Q$ - количество антенн (в тыс. шт., целочисленностью антенн пренебрегаем), $L−$ объем труда, а $K$ - объем капитала. Фирма является совершенным конкурентом как на рынке труда, так и на рынке антенн, цена 1 тыс. шт. равна 1. В настоящий момент в собственности фирмы есть 4 единицы капитала. Если фирма безразлична между несколькими объемами труда, то она выберет наибольший из них.
a) (12 баллов) Допустим, фирма не может изменить количество имеющегося у нее капитала. Выведите функцию спроса фирмы на труд $Ld(w)$ , показывающую, сколько единиц труда фирма наймет при каждом уровне зарплаты $w > 0$ .
б) (13 баллов) У фирмы появляется возможность арендовать дополнительно 5 единиц капитала, заплатив за это в сумме величину $S$ . Пусть $Smax(w)$ - максимальное значение $S$ , которое будет готова заплатить фирма «ЭПВВв» за аренду 5 единиц капитала при каждом $w > 0$ . Выведите функцию $Smax(w )$ и постройте ее график.
в) (5 баллов) Рассмотрите фразу «В данном случае функция $Smax(w)...$ , и значит, труд и капитал являются ... в производстве». Заполните первый пропуск словом «убывает» или «возрастает», а второй пропуск словом «субститутами» или «комплементами». Обосновывать свой выбор не нужно, в данном пункте проверяется только ответ.

Показать ответ и решение

a) При $K = 4$ производственная функция фирмы принимает вид

{ } {L2, L2 ≤ 4 Q(L,4)= min L2,4 = 2 4, L > 4

Составим функцию прибыли фирмы $π(L)$ . Фирма выбирает объем труда, так чтобы ее прибыль была максимальной.

{ { L2 − wL, L2 ≤4; L2− wL, L ≤ 2 π(L)= TR − TC = P ⋅Q − wL = 4− wL, L2 > 4 = 4− wL, L > 2

Мы не включили в прибыль расходы на капитал, потому что они уже понесены. Функция $L2 − wL$ является квадратичной, ветви параболы направлены вверх (Это Парабола с Ветвями Вверх, ЭПВВв). Парабола с ветвями вверх максимальна на отрезке $[0;2]$ обязательно либо в левом, либо в правом конце отрезка $1$ . Функция $4− wL$ же убывает, поэтому значения $L > 2$ точно не оптимальны.

Таким образом, максимум функџии прибыли может достигаться либо при $L = 0$ , либо при $L= 2$ , поэтому нам достаточно сравнить прибыль в этих точках. При $L= 0$ прибыль равна 0 , а при $L = 2$ прибыль равна $4− 2w$ . Сравнив значения прибылей, получаем, при $w ≤2$ оптимально выбирать $L = 2$ , а при $w > 2− L= 0$ . Искомая функция спроса на труд имеет вид:

{ Ld(w)= 2, w ≤20 w > 2

б) Фирма готова платить сумму $S$ за аренду 5 единиц капитала тогда и только тогда, когда ее прибыль от этого не уменьшается.

Рассчитаем прибыль фирмы в двух случаях: (1) фирма не арендует 2 единицы капитала; (2) фирма их арендует, платя $S$ . 1. Если фирма не арендует 5 единицы капитала, ее прибыль равна максимальной прибыли из пункта а). Она равна

{ π∗1 = 4− 2w, w ≤ 2 0, w > 2

2. Если фирма арендует 5 единиц капитала, ее максимальную прибыль можно найти так же, как в пункте а), только не для $K =4$ , а для $K =4 +5 = 9$ . Также нужно вычесть из прибыли $S$ . При $K = 9$ функция прибыли фирмы примет вид

{ 2 π(L)= L − wL − S, L≤ 3 9 − wL− S, L> 3

Фирма максимизирует ее по $L$ . Аналогично пункту а), максимум достигается либо при $L = 0$ , где прибыль равна $− S$ , либо при $L =3$ , где прибыль равна $9 − 3w − S$ . Получаем, что при $w ≤ 3$ оптимальным является $L= 3$ , при $w > 3− L =0$ . Значит, максимальная прибыль равна

{ ∗ 9 − 3w − S, w ≤ 3 π2 = − S, w > 3

$Smax(w )$ - это максимальное значение $S$ , при котором $π∗2 ≥ π∗1$ . Значит, - При $w ≤ 2Smax(w) = 9− 3w − 4+ 2w =5 − w$ . - При $2< w ≤ 3Smax(w) =9 − 3w − 0= 9− 3w$ .

- При $w > 3Smax(w)= 0 − 0 = 0$ .

Таким образом,

( |{ 5− w, 0< w ≤ 2 Smax(w)= 9− 3w, 2< w ≤ 3 |( 0, w > 3

График этой функции имеет вид

$PIC$

в) 1) «убывает», 2) «комплементами».

Пояснение (от участника оно не требуется): $Smax(w)$ является готовностью платить за капитал, то есть величиной, характеризующей спрос на капитал. Получаем, что на качественном уровне спрос на капитал убывает по цене труда (зарплате). Когда спрос на одно благо убывает по цене другого, блага являются дополняющими (комплементами).

Ответ:

а) ${ 2, w ≤ 20 Ld(w) = w > 2$

б) $(|5 − w, 0< w ≤ 2 Smax(w)= {9 − 3w, 2< w ≤ 3 |( 0, w > 3$

График предоставлен в решении

в) 1) "Убывает"2) "Комплементами"

Ошибка.
Попробуйте повторить позже

Задача 14#95280

В некой стране рынок грузовых автомобильных перевозок является рынком совершенной конкуренции. Спрос описывается уравнением $Q = 25− P$ , предложение имеет вид $P = 5$ . Перевозки сопровождаются вредными выбросами в атмосферу. Объем перевозок $Q$ влечет ущерб для экологии в денежном эквиваленте $2 aQ$ , где $a >0−$ параметр.

Государство задумалось о вмешательстве на данном рынке с целью увеличения общественного благосостояния. Министерство экономики подготовило список возможных мер, и среди них оказалась довольно неожиданная. Согласно расчетам министерства, общественное благосостояние увеличится, если принудительно объединить все фирмы, создав на этом рынке монополиста.
a) (17 баллов) Определите, какие значения может принимать параметр а в свете сказанного в предыдущем предложении.
б) (13 баллов) Определите значение параметра $a$ , если объединение фирм приведет к росту общественного благосостояния до максимально возможного уровня.

Для справки. Величина общественного благосостояния при объеме $Q$ равна сумме излишка потребителей (равного $2 CS = 0,5Q$ ) и прибыли фирм за вычетом ущерба для экологии. Считайте, что постоянные издержки отсутствуют.

Показать ответ и решение

a) Найдем, при каких $a$ общественное благосостояние при монополии больше, чем при конкуренции. 1) Определим, какое количество грузовых перевозок производится при совершенной конкуренции. Пересекая спрос и предложение, получаем, что $c Q = 25− P = 25− 5 =$ 20. 2) Определим величину общественного благосостояния при конкуренции. Излишек потребителей равен $2 CS =20 ∕2= 200$ (его можно посчитать и непосредственно площадь треугольника, образованного графиками спроса и предложения: $c CS = (25 − 5)⋅20∕2= 200($ см. рис. 6.1 $)$

Абсолютно эластичное предложение означает постоянные предельные издержки производства, которые равны $5 :MC =5$ . Поскольку $FC = 0$ , то $AC = 5$ , а значит, $P = AC$ , то есть (экономическая) прибыль фирм равна нулю.

Наконец, ущерб для экологии равен $a(Qc)2 = 400a$ . Таким образом, общественное благосостояние при совершенной конкуренции равно

SW c = CSc +0 − 400a= 200− 400a

3) Теперь найдем оптимум монополиста. Как мы выяснили, $MC = 5,F C = 0$ , поэтому общие издержки монополиста равны $TC(Q) =5Q$ . Монополист решает задачу максимизации прибыли:

π(Q )= (25 − Q )Q − 5Q = (20− Q )Q → maxQ

Графиком функции прибыли является парабола с ветвями вниз, вершина которой определяется объемом перевозок $Qm = 10$ .

Оптимум монополиста также можно было найти через равенство предельного дохода и предельных издержек: $MR (Q)= 25− 2Q = 5$ . Мы получим максимум, потому что это стандартная модель с линейным спросом, $MR$ убывает, и $MC$ постоянны. Также можно максимизировать прибыль как функцию от цены: $π(P )= (P − 5)(25− P)→$ $maxP$ , это парабола с ветвями вниз, вершина находится посередине между корнями, $P∗ = (25+ 5)∕2= 15$ , тогда $Q = 25− P∗ =10$ . 4) Определим величину общественного благосостояния при монополии. Величина излишка потребителя $CSm$ равна $(Qm )2∕2= 50$ . (Ее можно найти и непосредственно как площадь треугольника, образованного графиком спроса и ценой $P m = 15 :CSm =$ $(25− 15)⋅10∕2 =50$ .) При этом монополист получит прибыль $πm = (25− Qm )Qm − 5Qm =$ 100 и принесет ущерб экологии $a(Qm )2 = 100a$ .

Значит, величина общественного благосостояния при монополии равна

SW m = 50+ 100− 100a = 150 − 100a

. 5) Монополизация рынка приведет к увеличению благосостояния, так что

c m SW < SW 200 − 400a< 150− 100a 50 <300a 1 6 < a

б) 1) Определим, при каком объеме перевозок достигается максимальный уровень благосостояния. В общем виде излишек потребителя равен $2 CS(Q) =Q ∕2$ , а прибыль $π(Q) = (20− Q )Q$ . Таким образом, функция общественного благосостояния имеет вид

( ) SW (Q)= Q2∕2+ (20− Q)Q − aQ2 = 20Q− 1+ a Q2 2

Графиком функции общественного благосостояния является парабола с ветвями вниз, вершина которой определяется объемом перевозок $Q∗ = 12+02a$ . Аналогичный ответ также можно было получить, приравняв производную $SW (Q)$ к нулю и проверив критическую точку на максимум.

Итак, общественное благосостояние достигает своего максимального уровня при $Q ∗ = 12+02a$ 2) Теперь определим, при каком $\text{[math]}$ максимум общественного благосостояния достигается при монополии.

Способ 1 (более быстрый). Поскольку для достижения максимума общественного благосостояния необходимо, чтобы объем равнялся $∗ -20- Q = 1+2a$ , этот максимум достигается при монополии, если и только если монопольный выпуск равен как раз $Q ∗$ :

m ∗ Q = Q 10 = -20-- 1+ 2a

откуда $a= 12$ . Ответ: $a= 1∕2$ . Способ 2 (более длинный) Непосредственно приравняем максимальное общественное благосостояние к благосостоянию при монополии (которое мы уже нашли в пункте а)).

Максимально возможное благосостояние равно равно

∗ --20- 1+-2a( -20--)2 -200- SW (Q )= 201 +2a − 2 1+ 2a = 1 +2a

Приравняем его к монопольному:

-200- =SW m = 150− 100a 1+ 2a

Деля обе части на 100 и преобразовывая, получаем квадратное уравнение

2 4a − 4a +1 = 0 (2a− 1)2 =0

откуда $a= 1∕2$ .

Ответ:

а) $a > 1 6$

б) $1 a= 2$

Ошибка.
Попробуйте повторить позже

Задача 15#95284

В некоторой закрытой экономике предельная норма потребления убывает с ростом дохода, и функция потребления задается уравнением $√-- C = 4+ Yd$ , где $Yd−$ располагаемый доход домохозяйств, $C$ - их потребление. Инвестиции равны 16, а госзакупки и налоги изначально равны нулю. В данной задаче рассматриваются только аккордные налоги.
a) (5 баллов) Найдите равновесный уровень ВВП в данной экономике.
б) (5 баллов) Найдите уровень ВВП, если государство в ситуации пункта а) увеличит госзакупки на 10 единиц, не увеличивая налоги.
в) (5 баллов) Найдите уровень ВВП, если государство в ситуации пункта а) увеличит госзакупки на 22 единицы, не увеличивая налоги.
г) (6 баллов) Определите мультипликаторы госрасходов для политик в пунктах б) и в). Одинаковы ли они?
д) (9 баллов) Как известно, в стандартной модели (при линейной функции потребления) мультипликатор сбалансированного бюджета равен единице для любого размера увеличения госзакупок $ΔG ≥ 0$ . Верно ли это в данной задаче?

Показать ответ и решение

a) По основному макроэкономическому тождеству для закрытой экономики, $Y =$ $C + I + G$ . Поскольку изначально $√ ----- √ -- G = T = 0,Y = 4+ Y − 0+ 16+ 0,Y = 20 + Y$ . Это уравнение квадратное относительно $√-- x= Y$ , имеем $x2 − x − 20 = 0$ , откуда $x = 5$ (подходит только положительный корень). Значит, $2 Y = x =25$ .

б) Теперь уравнение на $Y$ запишется как $√----- √-- Y = 4+ Y − 0+ 16+ 10,Y = Y + 30$ . Это уравнение квадратное относительно $√-- x= Y$ , имеем $2 x − x − 30 = 0$ , откуда $x = 6$ (подходит только положительный корень). Значит, $2 Y = x =36$ .

в) В этом случае уравнение на $Y$ запишется как $Y = 4+ √Y-−-0+ 16+ 22,Y = √Y-+42$ . Это уравнение квадратное относительно $x= √Y-$ , имеем $x2 − x − 42 = 0$ , откуда $x = 7$ (подходит только положительный корень). Значит, $Y = x2 =49$ .

г) Мультипликатор госрасходов равен $ΔY- multG = ΔG$ . Для пункта б) имеем

multG = ΔY-= 36-− 25 = 11 ΔG 10− 0 10

Для пункта в) имеем

ΔY- 49-− 25 12 multG = ΔG = 22− 0 = 11

Поскольку $11 12 10 ⁄= 11$ , мультипликаторы не равны.

д) При сбалансированном бюджете размеры увеличения госзакупок и налогов одинаковы, $ΔG = ΔT$ . (В данном случае это означает, что просто $G = T$ .) Найдем равновесный ВВП при каждом $ΔG$ в данной задаче.

Имеем

√ ------- √ ------- Y = 4+ Y − ΔG + 16+ ΔT = 4+ Y − ΔG + 16+ ΔG Y − ΔG = 20+ √Y-−-ΔG-

Сделав замену $√ ------- Y − ΔG = x$ , получаем уравнение $x2− x− 20= 0$ , которое мы уже решили в пункте а): $x= 5$ . Поэтому $Y − ΔG = x2 = 25$ , и окончательно

Y = 25+ ΔG

Поэтому при росте госзакупок и налогов одновременно на $ΔG$ , ВВП вырастет ровно на то же $ΔG$ . Следовательно, мультипликатор сбалансированного бюджета в данной задаче, так же как и в стандартной модели, равен единице для любого размера увеличения госзакупок.

Ответ:

а) $Y = 25$

б) $Y = 36$

в) $Y = 49$

г) $11, 12 10 11$ , не равны

д) "Неверно"

Ошибка.
Попробуйте повторить позже

Задача 16#95288

В России действует налог на добычу полезных ископаемых (НДПИ). В случае нефти он взимается как потоварный налог за каждую добытую тонну нефти, при этом ставка налога $t$ зависит от мировой цены на нефть. В этой задаче мы рассмотрим модель, в рамках которой можно определить оптимальную ставку НДПИ в зависимости от мировой цены.

Предположим, что в некой стране внутренний спрос на нефть описывается уравнением $P = 90− 3Q$ , а внутреннее предложение - уравнением $P = 30+ Q$ . Страна может экспортировать на мировой рынок любое количество нефти по цене $x≥ 0$ , но импортировать нефть не может. Государство вводит НДПИ на нефть как потоварный налог по ставке $t≥ 0$ . Налог взимается с каждой добытой единицы нефти независимо от того, где она продана. Государство максимизирует сумму налоговых сборов. Если государство безразлично между двумя ставками налога, оно выбирает наименьшую из них.

Пусть $t∗(x)$ - ставка налога, которую назначит государство в зависимости от $x$ . Выведите функцию $∗ t(x)$ для всех $x ≥0$ и постройте ее график.

Показать ответ и решение

После введения НДПИ по ставке $t$ возможны два случая: 1) нефть поставляется только на внутренний рынок; 2) нефть поставляется как на внутренний, так и на внешний рынок.

Найдем, при каких $t$ и $x$ реализуется каждый из двух случаев. Прямая функция внутреннего спроса имеет вид $Qd(P)= 30− P∕3$ . После введения НДПИ кривая предложения примет вид $P = 30+ Q + t$ , то есть $Qs(P)= P − 30− t$ . Нефть будет поставляться на внешний рынок тогда и только тогда, когда $Q (x)< Q (x) d s$ , то есть $30− x∕3< x − 30 − t$ , откуда $t< 4x∕3− 60$ .

Теперь найдем зависимость равновесного объема добычи (производства) от $t$ . При $t< 4x∕3− 60$ нефть будет экспортироваться, общий объем добычи будет определяться мировой ценой, $Q= Qs (x)= x − 30 − t$ . При $t≥ 4x∕3− 60$ нефть будет продаваться только внутри страны, а значит, объем будет определяться внутренним равновесием: $90 − 3Q = 30+ Q +t$ , откуда $Q= (60− t)∕4$ . Подытоживая,

{x − 30 − t, t< 4x∕3− 60 Q (t)= (60− t)∕4, t≥ 4x∕3− 60

Значит, налоговые сборы по НДПИ будут равны

{ T(t)= tQ (t)= t(x− 30− t), t <4x∕3− 60 t(60− t)∕4, t ≥4x∕3− 60

Государство максимизирует эту функцию по $t$ . Найдем точку глобального максимума $T(t)$ при каждом $x ≥ 0$ . Заметим, что функция $T(t)$ на каждом из двух участков является квадратичной, ветви парабол направлены вниз. Легко проверить, что функция является непрерывной в точке переключения с одной параболы на другую.

Чтобы установить промежутки монотонности функции $T (t)$ , найдем точки вершин парабол, а также значения $x$ , при которых вершины парабол находятся на актуальных для этих парабол участках. Последнее важно, потому что если обе вершины парабол находятся за пределами участков, на которых эти параболы актуальны, то $T (t)$ будет максимальна не в вершине какой-либо из двух парабол, а в точке стыковки двух парабол.

Вершиной левой параболы является $t1 = (x − 30)∕2$ , вершиной правой параболы $t2 = 30$ . Эти точки можно также найти, приравнивая производную сборов к нулю. Вершина левой параболы принадлежит актуальному для этой параболы участку при $(x− 30)∕2 < 4x∕3 − 60,x> 54$ . Вершина правой параболы принадлежит актуальному для этой параболы участку при $30 >4x∕3− 60,x< 67,5$ . Кроме того, заметим, что при $x ≤ 454x∕3− 60≤ 0$ , и потому левого участка при $x≤ 45$ просто нет (это случай, когда мировая цена меньше чем равновесная в закрытой экономики, поэтому даже без налога экспорта не будет).

Получаем 4 случая. 1. При $x ≤ 45$ левого участка нет, графиком $T(t)$ является просто парабола, оптимальной ставкой налога является $t∗ = t2 =30$ . 2. При $x ∈(45;54]$ левый участок есть, но вершина левой параболы находится вне левого участка (справа от него). Значит, на левом участке функция $T (t)$ монотонно возрастает. Вершина правой правой параболы принадлежит правому участку. Значит, максимум функции $T(t)$ достигается в вершине правого участка, $∗ t = t2 = 30$ . 3. При $x∈ (54;67,5]$ вершины обеих парабол принадлежат соответствуюшим участкам. Значит, максимум $T(t)$ достигается в одной из вершин - в той, где значение функции больше. Сравним эти значения. $T (t1)= T((x− 30)∕2)= (x− 30)2∕4$ . $T (t2)= T(30)= 900∕4.T (t1)> T (t2)$ при $(x− 30)2∕4 >900∕4,(x− 30)2 > 900,x > 60$ . Значит, при $x> 60$ оптимальной ставкой будет $t∗ = t1 = (x− 30)∕2$ , при $x< 60$ оптимальной ставкой будет $t∗ = t2 = 30$ . При $x= 30$ государство безразлично. По условию, оно выберет наименьшую ставку, то есть $t1 = (60− 30)∕2 = 15$ . 4. При $x> 67,5$ вершина левой параболы принадлежит левому участку, вершина правой параболы лежит левее правого участка. Значит, на правом участке функция монотонно убывает, а максимум достигается в вершине левого участка, $∗ t = t1 = (x− 30)∕2= x∕2− 15$ .

В итоге, получаем, что оптимальной ставкой налога при каждой мировой цене $x ≥ 0$ является

{ t∗(x) = 30, x< 60 x∕2− 15, x≥ 60

График этой функции выглядит следующим образом:

$PIC$

Ответ:

${ ∗ 30, x< 60 t (x) = x∕2− 15, x≥ 60$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 17#95293

В государстве Ругриград национальной валютой является ругрик. На валютном рынке функция спроса на ругрики имеет вид $QD (P )= 100 − P$ , где $P$ - валютный курс ругрика (цена одного ругрика, выраженная в единицах иностранной валюты), $Q−$ количество ругриков (в млн). Функция предложения ругриков на валютном рынке, в свою очередь, зависит от ставки процента $r$ в Ругриграде и имеет вид $S Q (P )= kr+ P$ , где $k$ - некоторый коэффициент. Ставка процента $r$ измеряется в процентах, а не в долях, то есть если $r = 10%$ , то в уравнение нужно подставлять число 10. Частное потребление в Ругриграде задается как $C = 20+ 0,5Yd$ , где $Yd$ - располагаемый доход, чистые налоги и госрасходы автономны и равны, соответственно, $T = 50$ и $G = 30$ . Инвестиции отрицательно зависят от ставки процента ( $I =40 − r$ ), а чистый экспорт отрицательно зависит от валютного курса ругрика и задается функцией $NX = 10$ $0,5P$ .
a) (2 балла) Пользуясь экономической интуицией, отметьте наиболее вероятный знак коэффициента $k :+$ или -. Объяснение приводить не нужно. В дальнейшем решении пользуйтесь вашим предположением относительно знака коэффициента $k$ .
б) (10 баллов) Пусть $|k|= 1$ , а ставка процента $r = 10%$ . Чему равны равновесный валютный курс ругрика $P$ и равновесный выпуск Ругриграда?
в) (4 балла) Спрос на ругрики упал до уровня $QD(P)= 94− P$ . На сколько процентных пунктов и как (увеличить/уменьшить) Центральный Банк Ругриграда (ЦБР) должен изменить ставку процента, чтобы вернуть курс ругрика к прежнему уровню?
г) (4 балла) Предположим, ЦБР изменил ставку процента до уровня, определенного в в). На сколько и как (увеличить/уменьшить) нужно теперь изменить налоги, чтобы вернуть ВВП на исходный уровень, сохраняя уровень валютного курса?

Показать ответ и решение

a) Ответ: - (минус).

Пояснение (от участника оно не требуется): при прочих равных, рост ставки процента в стране увеличивает стимулы агентов к сбережению денег в национальной валюте - ругриках. Таким образом, предложение ругриков - желание их продавать должно снижаться. Значит, $k < 0$ .

б) На валютном рынке должен наблюдаться баланс спроса и предложения ругриков, $D S Q (P) =Q (P)$ . Из условия мы знаем, что $D Q (P)= 100− P$ , а из предыдущего пункта ясно, что $QS(P)= − 10 + P$ . Соответственно, в равновесии верно, что $100− P = −10+ P$ , откуда $P =55$ - равновесный валютный курс ругрика.

Теперь запишем основное макроэкономическое тождество для открытой экономики: $Y = C + I + G+ NX = 20+ 0,5Yd+ 40− r+ 30+ 10− 0,5P = 100 +0,5Yd− r− 0,5P$ . Поскольку в Ругриграде налоги автономны, располагаемый доход оказывается равен $Yd = Y − T = Y − 50$ . Также из условия известно, что $r = 10$ , а из предыдущей части решения мы знаем, что $P = 55$ . Подставляя эти результаты в уравнение, получим $Y = 75+ 0,5Y − r− 0,5P =75 +0,5Y − 10− 0,5 ⋅55$ , и решая его относительно $Y$ имеем, что $Y = 75$ - равновесный выпуск Ругриграда.

в) Пусть ставка процента равна $r$ . Тогда новый равновесный валютный курс ругрика находится из уравнения $QD (P)= QS (P )$ , то есть $94− P =− r+ P$ , откуда $P = 47+ 0,5r$ . ЦБР хочет, чтобы было выполнено соотношение $P = 47+ 0,5r = 55$ , откуда новое значение ставки процента равно $r = 16$ . Изначально ставка процента была равна $10%$ , а значит, чтобы добиться своей цели, Центральный Банк должен увеличить ставку процента на 6 процентных пунктов.

г) В новых условиях верно, что $r = 16$ и $P = 55$ . Из решения пункта б) мы знаем, что основное макроэкономическое тождество для Ругриграда может быть записано в виде уравнения $Y = 100+ 0,5(Y − T)− r− 0,5P$ . Государство хочет вернуть выпуск на исходный уровень, то есть добиться $Y = 75$ . Подставляя $Y,r$ и $P$ в уравнение и решая его относительно $T$ , получим, что $T = 38$ . Исходный уровень налогов равен 50, поэтому для достижения своей цели государству следует уменьшить налоги на 12

Ответ:

а) ’-’

б) $P = 55,Y = 75$

в) увеличить на 6 процентных пунктов

г) уменьшить на 12

Ошибка.
Попробуйте повторить позже

Задача 18#95295

Авиарейсы из города N-ска в Москву осуществляет единственная авиакомпания «N-авиа». Спрос на ее услуги предъявляют две группы пассажиров - пенсионеры и непенсионеры. Месячный спрос пенсионеров на авиабилеты описывается уравнением $Q = 44− P$ , а месячный спрос непенсионеров - уравнением $Q = 80− P$ . Месячная функция издержек авиакомпании имеет вид $T C = 20Q + 500$ .

Продавать билеты пенсионерам и непенсионерам по разным ценам законом не запрещено, но изначально авиакомпания этого не делает, потому что продает билеты только через интернет и не имеет технической возможности проверять наличие пенсионных удостоверений.
a) (10 баллов) Найдите единую цену на билет, которую установит компания в изначальной ситуации.
б) (6 баллов) Авиакомпания может арендовать офис продаж в одном из городских торговых центров. Продавая билеты в офисе, фирма сможет проверять наличие пенсионных удостоверений, и, соответственно, назначать для пенсионеров и непенсионеров разные цены. Определите максимальное значение месячной арендной платы $Rmax$ , которое компания будет готова платить за аренду офиса.
в) (4 балла) Допустим, наличие офиса не только позволяет назначать для пенсионеров и непенсионеров разные цены, но и увеличивает в целом узнаваемость авиакомпании - в случае открытия офиса спрос непенсионеров вырастет до $Q = 90− P$ . Найдите значение $Rmax$ в этих условиях

Показать ответ и решение

а) Найдем функцию рыночного спроса. Поскольку при ценах $P ∈(44;80)$ покупают билеты только непенсионеры, спрос имеет вид

{ { 80− P +44 − P, P ≤ 44; 124 − 2P, P ≤44; Q (P )= 80− P, P ∈(44;80] = 80− P, P ∈(44;80]

Дальше можно решать двумя способами - максимизацией прибыли по цене или по количеству.

Способ 1 (максимизация по цене). Составим функцию прибыли фирмы $π(P)$ .

{ π(P )= Q(P)⋅P−T C(Q(P))= Q(P)P− 20Q (P )−500= 164P − 2P 2− 2980, P ≤ 44 100P − P 2− 2100, P ∈ (44;80]

Найдем цену $P∗$ , при которой прибыль максимальна. Функция прибыли на каждом из участков является квадратичной, ветви парабол направлены вниз. Поэтому максимум на каждом из участке достигается в вершине соответствующей параболы, если она принадлежит этому участку.

Найдем эти вершины. - На участке $[0;44],PB = (−164)∕(−2⋅2)= 41$ , что принадлежит этому участку. - На участке $(44;80]PB = (−100)∕(−2)= 50$ , что принадлежит этому участку.

Значит, обе цены 41 и 50 являются точками локального максимума прибыли. Глобально оптимальной будет та из этих двух цен, при которой прибыль больше. Рассчитаем эту прибыль.

π (41)= (124 − 2 ⋅41)(41− 20) − 500= 382 π(50) = (80− 50)(50− 20)− 500= 400

Поскольку $400> 382$ , оптимальной является цена $P∗ = 50$ . Авиакомпания назначит цену, при которой пенсионеры не будут пользоваться ее услугами.

Способ 2 (максимизация по количеству). Найдем обратную функцию рыночного спроса $P (Q )$ из уравнения $Q (P)$ .

{ P (Q)= 80 − Q, Q ≤36 62 − Q ∕2, Q ∈(36;124]

Точку излома $Q = 36$ получаем, подставив цену излома $P = 44$ в $Q(P)$ . Составим функцию прибыли $π(Q)$ .

{ 2 π(Q)= P(Q) ⋅Q − TC (Q )= 60Q − Q − 500, Q ≤ 36 42Q − Q2 ∕2 − 500, Q ∈ (36;124]

На каждом из двух участков функция является квадратичной, ветви параболы направлены вниз. При $Q ≤ 36$ вершиной параболы является $Q в = (− 60)∕(−2)= 30$ , при $Q >36$ вершина находится в точке $QB = −(42)∕(−2⋅0,5) =42$ . Обе вершины принадлежат соответствующим участкам, значит, на каждом из участков максимум достигается именно в соответствующей вершине.

Также точки локального максимума $Q = 30$ и $Q = 42$ можно найти из приравнивания $MR$ и $MC$ . Функция $MR (Q)$ на каждом из участков вдвое более крута, чем функция $P (Q )$ :

{ MR (Q)= 80− 2Q, Q < 36 62− Q, Q ∈ (36;124]

Решая уравнение $MR (Q )= 20$ , находим его два корня $Q =30$ и $Q= 42$ . Это точки локального максимума прибыли, потому что $MR$ убывает в окрестности этих точек, а $\text{[math]}$ постоянны.

Чтобы найти глобальный максимум прибыли, сравним прибыль при $Q = 30$ и $Q = 42$ .

π(30)= 60⋅30− 302− 500 =400 2 2 π(42)= 42 − 42 ∕2− 500= 382.

Значит, прибыль максимальна при $Q∗ = 30$ , что соответствует цене $P ∗ = 80− 30= 50$ .

б) Фирма будет готова платить за аренду офиса сумму не большую, чем прирост ее прибыли от того, что она сможет назначать две разные цены, а не одну единую. Найдем максимальную прибыль фирмы, если она может назначать две разные цены.

Способ 1 (максимизация по ценам). Пусть $P1$ - цена для пенсионеров, а $P2$ - для всех остальных. Тогда прибыль фирмы как функция этих двух цен примет вид

π(P1,P2) =(44− P1)P1+ (80− P2)P2− 20(44 − P1 +80 − P2)− 500= =(44− P1)(P1− 20)+(80− P2)(P2− 20)− 500

Как видим, функция прибыли разбивается на сумму двух слагаемых, каждое из которых является функцией только от своей цены. Прибыль будет максимальна, когда каждое из слагаемых будет максимально. Поскольку каждое из слагаемых является квадратичной функцией и ветви парабол направлены вниз, максимум каждого из слагаемых достигается в вершине соответствуюшей параболы. Отсюда $P∗1 = 32$ , $P∗2 = 50$ (вторую вершину мы уже нашли в пункте а)).

Максимальная прибыль (без учета расходов на аренду) равна $π(32,50)= (44−$ $32)(32 − 20)+ (80 − 50)(50− 20)− 500= 544$

Значит, фирма будет готова платить за аренду офиса не больше, чем

Rmax = 544− 400= 144

Эту сумму можно было найти чуть проще, заметив, что поскольку фирма назначает для непенсионеров ту же цену, что и в пункте а), (переменная) прибыль от непенсионеров та же, а значит, $Rmax$ просто равно вновь полученной прибыли от пенсионеров, то есть $(44 − 32)(32 − 20)= 144$ .

Способ 2 (максимизация по количествам). Пусть $Q1$ - объем покупок пенсионеров, $Q2$ - непенсионеров. Тогда прибыль фирмы как функция от $Q1$ и $Q2$ есть

π(Q1,Q2)= (44 − Q1 )Q1+ (80− Q2)Q2− 20(Q1+ Q2)− 500= = (24Q1 − Q21)+ (60Q2− Q22)− 500

Как видим, функция прибыли разбивается на сумму двух слагаемых, каждое из которых является функцией только от своего количества. Прибыль будет максимальна, когда каждое из слагаемых будет максимально. Поскольку каждое из слагаемых является квадратичной функцией и ветви парабол направлены вниз, максимум каждого из слагаемых достигается в вершине соответствующей параболы. Отсюда $∗ Q1 =12$ , $∗ Q 2 = 30$ (вторую вершину мы уже нашли в пункте а)).

Также можно эти объемы найти из приравнивания предельного дохода для каждой группы с предельными издержками: $MR (Q )= 44 − 2Q = MC = 20,MR (Q )= 1 1 1 2 2$ $80− 2Q2 = MC = 20$ . При таком решении $Qi$ проверкой достаточных условий максимума является указание на то, что функции $MR$ убывают, а $MC$ постоянны. Максимальная прибыль (без учета расходов на аренду) равна $π(12,30)= 544$ . Значит, фирма будет готова платить за аренду офиса не больше, чем

Rmax = 544− 400= 144

в) Пересчитаем максимальную прибыль в случае открытия офиса. Она находится так же, как в пункте б), но с новым спросом непенсионеров. Поскольку спрос пенсионеров тот же, что в б), мы уже знаем оптимальную цену для них $⋆ − P 1 = 32$ (оптимальный объем $∗ Q1 = 12$ ).

Найдем новый оптимум при обслуживании непенсионеров.

Способ 1 (максимизация по цене). Новую оптимальную цену для непенсионеров находим из максимизации функции $(90− P)(P − 20)$ . Эта функция квадратичная, ветви параболы направлены вниз, значит, максимум достигается в вершине, откуда $P2∗= 55$ .

Способ 2 (максимизация по количеству). Новый оптимальный объем для непенсионеров находим из максимизации функции ( $90 − Q )Q − 20Q$ . Эта функция квадратичная, ветви параболы направлены вниз, значит, максимум достигается в вершине, откуда $Q∗2 =35$ . Также этот объем можно найти из приравнивания $MR = 90− 2Q$ и $MC = 20$ .

Значит, в случае открытия офиса прибыль будет равна

π = 144+ (90− 55)(55− 20) − 500= 869.

Отсюда $Rmax = 869− 400= 469$ .

Ответ:

а) $P ∗ = 50$

б) $Rmax =144$

в) $Rmax =469$

Ошибка.
Попробуйте повторить позже

Задача 19#95298

В странах Линея и Квадратия могут производиться товары X и Y. КПВ страны Линея имеет вид $y1 = 280− 2x1$ . КПВ страны Квадратия имеет вид $y2 = 252− x22∕7$ . В обеих странах товары потребляют только в комплектах. Один комплект состоит из одной единицы товара $X$ и пяти единиц товара $Y$ .
a) (5 баллов) Допустим, страны никак не взаимодействуют друг с другом. Найдите максимально возможное суммарное потребление комплектов в двух странах.
б) (15 баллов) Теперь допустим, что страны могут сотрудничать, то есть договориться о совместной стратегии производства. Найдите максимальное возможное суммарное потребление комплектов в двух странах. На сколько комплектов оно больше, чем в пункте а)? Подсказка: пункт б) можно решить как с помощью нахождения суммарной КПВ, так и без него.

Показать ответ и решение

Ответ:

а) 68 комплектов

б) 77 комплектов, на 9 больше, чем в пункте а).

Ошибка.
Попробуйте повторить позже

Задача 20#95317

Показать ответ и решение

a) Исходя из соотношения товаров в комплектах, имеем $y1 =5x1$ и $y2 =5x2$ . Подставим в уравнения КПВ и преобразуем:

5x1 = 280− 2x1, 5x2 = 252 − x22∕7 7x1 = 280. x22∕7+ 5x2− 252 = 0.

Из первого уравнения получаем $⋆ x1 = 40$ , в Линее потребляется 40 комплектов. Из второго уравнения:

∘ ----------- √ --- x = −5±---25+-4⋅252∕7-= −5-±--169= −-5±-13. 2 2∕7 2∕7 2∕7

Нас интересует положительный корень $∗ x2 = 8∕(2∕7)= 28$ . Это и есть количество комплектов, потребляемых в Квадратии.

Общее количество комплектов в двух странах равно $40+ 28= 68$ . Графики КПВ (Рис. 3.1) для полного решения необязательны.

б) Способ 1 (не требует сложения КПВ). Составим систему ограничений, которая будет учитывать и КПВ обеих стран, и необходимость производить комплекты, и преобразуем ее так, чтобы выразить $x1$ через $x2$ :

( { { yy1 == 228502−− 2xx12∕,7, y1+ y2 = 280− 2x1+ 252− x22∕7 ( y21+ y2 = 5(x21 +x2). y1+ y2 = 5(x1+ x2); 2 1- 2 5 5(x1+ x2)= 280 − 2x1 +252− x2∕7; x1 =− 49x2− 7x2 +76

Количество комплектов, произведенное в странах, равно количеству произведенного товара X , то есть $(x1 +x2)$ . Его и нужно максимизировать при указанных выше ограничениях. Запишем выражение для этого количества:

( ) x1+ x2 = − 1-x22− 5x2+ 76 +x2 =− 1-x22+ 2x2+ 76. 49 7 49 7

Это парабола с ветвями вниз, ее максимум достигается при $x2 = (− 2∕7)∕(−2∕49)= 7$ . Отсюда получаем

1 2 5 x1 = − 49 ⋅7 − 7 ⋅7+ 76= −1− 5+ 76= 70

Оба объема производства X меньше максимально возможных в своих странах, поэтому найденные точки действительно лежат на страновых КПВ.

Общее количество комплектов равно общему количеству товара X и составляет $70+ 7 =77$ . Это на 9 комплектов больше, чем в пункте а).

Способ 2. Построим суммарную КПВ. Альтернативная стоимость товара $X$ в Линее всегда равна 2 , а в Квадратии является переменной величиной, равной модулю производной $y2$ по $x2 : 27x2$ . При значениях $x2 < 7$ альтернативная стоимость в Квадратии меньше, товар X нужно производить там. При б´ольших $x2$ производство каждой единицы X в Квадратии становится дороже, чем в Линее, поэтому нужно переключиться на производство X в Линее, а вернуться в Квадратию тогда, когда производственные возможности X в Линее будут исчерпаны.

Таким образом, уравнение общей КПВ имеет вид:

({ (280 − 2⋅0)+[252−[ X2∕7], ] X ≤ 7 (в Линее производится только Y) Y = (280 − 2(X − 7))+[ 252− 72∕7 , ] 7 < X < 147 (Х и Y производятся везде) ( (280 − 2⋅140)+ 252− (X − 140)2∕7 , X ≥ 147 (весь Y производится в Квадратии)

В каждом уравнении выражение в круглых скобках - количество единиц товара Y, произведенное в Линее, а в квадратных скобках - в Квадратии. Выражения записаны так, чтобы было видно, какое значение $x$ подставляется в уравнение КПВ каждой страны.

Подставим условие на соотношение товаров $Y = 5X$ в комплекте в каждый участок, при этом упростив правые части:

( 2 |{5X = 532− X ∕7, если X ≤ 7 |5X = 539− 2X, если 7 < X < 147 (5X = 252− (X − 140)2∕7, если X ≥ 147

Поскольку КПВ - убывающая функция, а $Y =5X$ - возрастающая, у них может быть не более одного пересечения. Решим самое простое уравнение - второе, получим $X = 77$ , что попадает в интервал $(7;147)$ . Можно (но не обязательно) убедиться, что решение первого уравнения $X ≈ 46$ на соответствующий участок не попадает, а третье уравнение и вовсе не имеет корней (это видно на Рис. 3.2, где «недостающие» части парабол нарисованы светлыми линиями). Значит, $X = 77$ и есть оптимальное производство товара X и оптимальное количество комплектов. Общее количество увеличится по сравнению с пунктом а) на 9.

Сложить КПВ можно и другим (более длинным) способом, не прибегая к сравнению альтернативных издержек. По определению, уравнение суммарной КПВ $Y (X )$ показывает максимальный суммарный уровень производства товара $Y$ при данном суммарном производстве товара $X$ . Значит, $Y(X )$ можно получить, решив оптимизационную задачу (*):