Ошибка.
Попробуйте повторить позже
Пятиугольник вписан в окружность. При этом
— точка пересечения
его диагоналей
и
Известно, что
— параллелограмм.
а) Докажите, что две стороны пятиугольника равны.
б) Найдите , если известно, что
Источники:
а) Так как — параллелограмм, то
и
Тогда
— трапеция, так как
и
Вокруг трапеции описана окружность, следовательно, она
равнобедренная, в которой
Значит, в пятиугольнике равны стороны
и
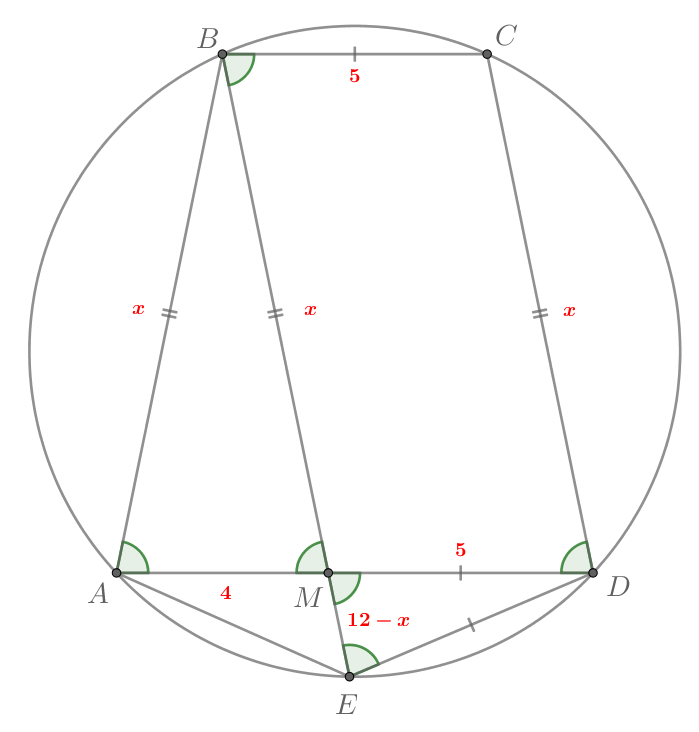
б) Аналогично пункту а) получаем, что — равнобедренная трапеция, в
которой
и
Так как по условию — параллелограмм, то
Тогда
Пусть По свойству пересекающихся хорд
и
в
окружности:
Заметим, что если то
Тогда в
стороны будут
равны 5, 5 и 10, что невозможно по неравенству треугольника.
Значит,
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Пятиугольник вписан в окружность. Известно, что
а) Докажите, что
б) Найдите длину диагонали если
Источники:
а) Равные хорды и
стягивают равные дуги, следовательно, вписанные
углы, опирающиеся на них, равны, то есть
Тогда накрест
лежащие углы, образованные прямыми
и
и секущей
равны,
следовательно,
Равные хорды и
стягивают равные дуги, следовательно, вписанные
углы, опирающиеся на них, равны, то есть
Тогда накрест
лежащие углы, образованные прямыми
и
и секущей
равны,
следовательно,
Пусть — точка пересечения диагоналей
и
Тогда в
четырехугольнике
известно, что
и
значит,
— параллелограмм. Следовательно,
и
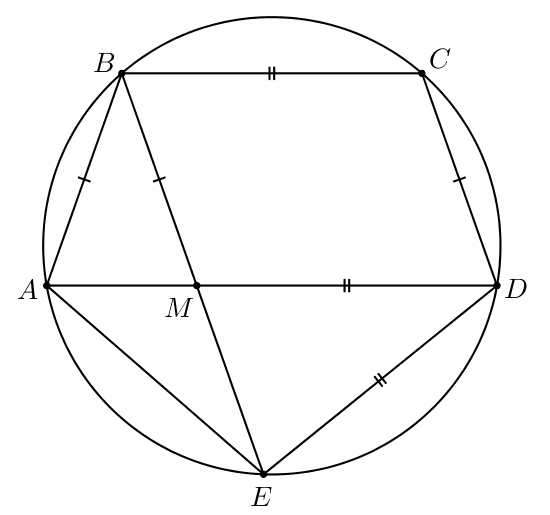
В четырехугольнике мы знаем, что
и
Значит,
—
равнобедренная трапеция. Диагонали равнобедренной трапеции равны, поэтому
В четырехугольнике мы знаем, что
и
Значит,
—
равнобедренная трапеция. Диагонали равнобедренной трапеции равны, поэтому
Таким образом,
б) В пункте а) мы узнали, что значит,
Тогда по свойству пересекающихся хорд и
в окружности:
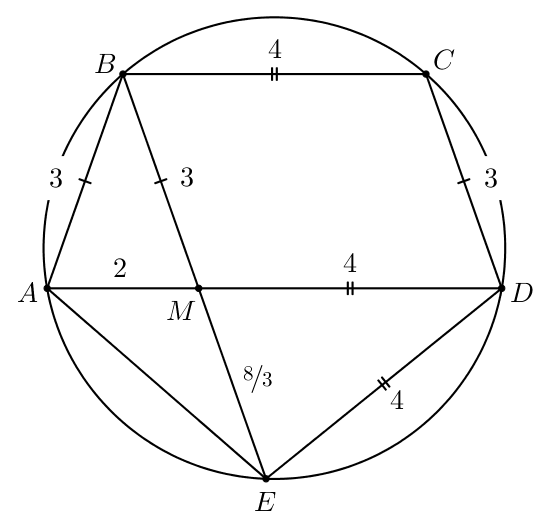
Значит,
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
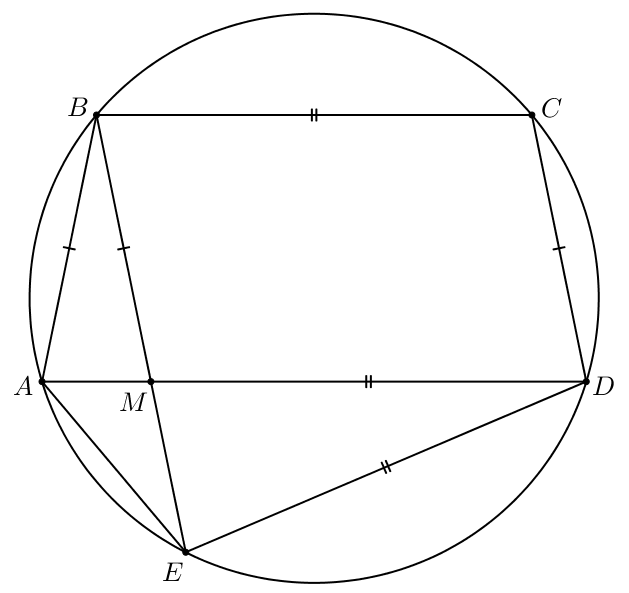
Ошибка.
Попробуйте повторить позже
Пятиугольник вписан в окружность. Известно, что
а) Докажите, что
б) Найдите длину диагонали если
Источники:
а) Равные хорды и
стягивают равные дуги, следовательно, вписанные
углы, опирающиеся на них, равны, то есть
Тогда накрест
лежащие углы, образованные прямыми
и
и секущей
равны,
следовательно,
Равные хорды и
стягивают равные дуги, следовательно, вписанные
углы, опирающиеся на них, равны, то есть
Тогда накрест
лежащие углы, образованные прямыми
и
и секущей
равны,
следовательно,
Пусть
— точка пересечения диагоналей
и
Тогда в четырехугольнике
известно, что
и
значит,
— параллелограмм. Следовательно,
и
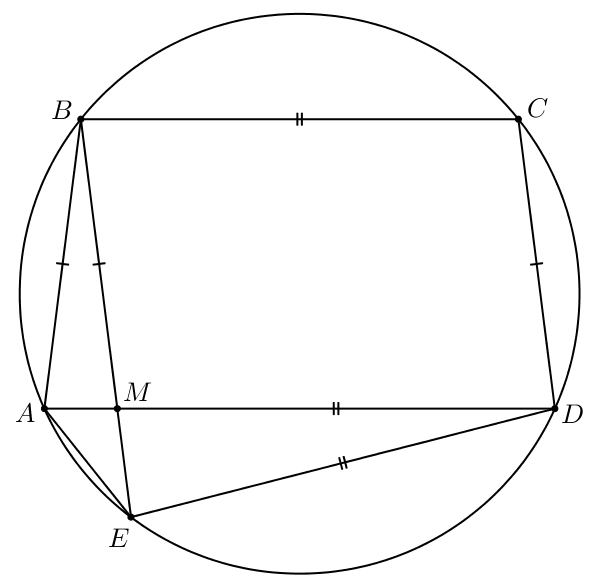
В четырехугольнике мы знаем, что
и
Значит,
—
равнобедренная трапеция. Диагонали равнобедренной трапеции равны, поэтому
В четырехугольнике мы знаем, что
и
Значит,
—
равнобедренная трапеция. Диагонали равнобедренной трапеции равны, поэтому
Таким образом,
б) В пункте а) мы узнали, что значит,
Тогда по свойству пересекающихся хорд и
в окружности:
Значит,
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
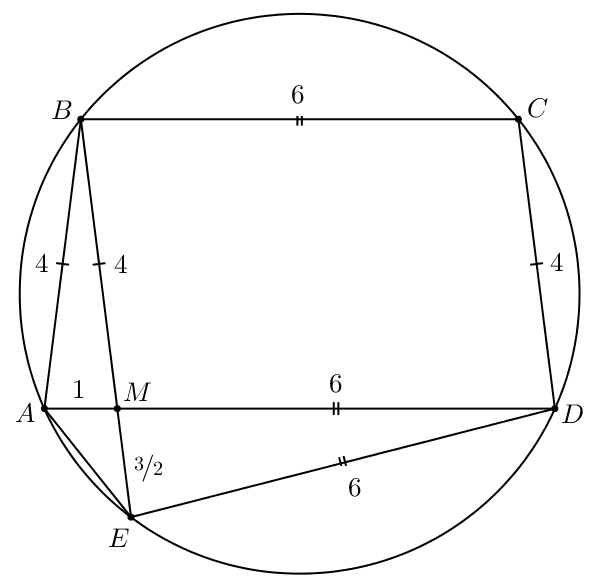
Ошибка.
Попробуйте повторить позже
Пятиугольник вписан в окружность. Известно, что
а) Докажите, что
б) Найдите длину диагонали если
Источники:
а) Равные хорды и
стягивают равные дуги, следовательно, вписанные
углы, опирающиеся на них, равны, то есть
Тогда накрест
лежащие углы, образованные прямыми
и
и секущей
равны,
следовательно,
Равные хорды и
стягивают равные дуги, следовательно, вписанные
углы, опирающиеся на них, равны, то есть
Тогда накрест
лежащие углы, образованные прямыми
и
и секущей
равны,
следовательно,
Пусть — точка пересечения диагоналей
и
Тогда в
четырехугольнике
известно, что
и
значит,
— параллелограмм. Следовательно,
и
В четырехугольнике мы знаем, что
и
Значит,
—
равнобедренная трапеция. Диагонали равнобедренной трапеции равны, поэтому
В четырехугольнике мы знаем, что
и
Значит,
—
равнобедренная трапеция. Диагонали равнобедренной трапеции равны, поэтому
Таким образом,
б) В пункте а) мы узнали, что значит,
Тогда по свойству пересекающихся хорд и
в окружности:

Значит,
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Окружность с центром в точке касается сторон угла с вершиной
в точках
и
Отрезок
— диаметр этой окружности.
а) Докажите, что прямая параллельна биссектрисе угла
б) Найдите если
Источники:
а) Центр окружности, вписанной в угол, лежит на его биссектрисе, так как он
равноудален от сторон этого угла. Тогда — биссектриса угла
Также
центр
лежит на диаметре
Заметим, что как отрезки касательных, проведенных к
окружности из одной точки, а значит, треугольник
— равнобедренный.
Поэтому его биссектриса из вершины
также является и высотой, то есть
При этом как опирающийся на диаметр, а значит,
Таким образом,
и
следовательно,

б) Рассмотрим четырехугольник В нем
так
как радиусы
и
проведенные в точку касания, перпендикулярны
касательным
и
соответственно. Значит, сумма противоположных углов
четырехугольника
равна
следовательно,
— вписанный.
Тогда
как углы, опирающиеся на одну дугу описанной около
этого четырехугольника окружности.
Рассмотрим треугольники и
В них
и
Значит,
по двум углам. Запишем отношение
подобия:
По теореме Пифагора для прямоугольного треугольника
Тогда так как — центр окружности, то
Таким образом,
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Окружность с центром в точке касается сторон угла с вершиной
в точках
и
Отрезок
— диаметр этой окружности.
а) Докажите, что прямая параллельна биссектрисе угла
б) Найдите если
Источники:
а) Центр окружности, вписанной в угол, лежит на его биссектрисе, так как он
равноудален от сторон этого угла. Тогда — биссектриса угла
Также
центр
лежит на диаметре
Заметим, что как отрезки касательных, проведенных к
окружности из одной точки, а значит, треугольник
— равнобедренный.
Поэтому его биссектриса из вершины
также является и высотой, то есть
При этом как опирающийся на диаметр, а значит,
Таким образом,
и
следовательно,

б) Рассмотрим четырехугольник В нем
так
как радиусы
и
проведенные в точку касания, перпендикулярны
касательным
и
соответственно. Значит, сумма противоположных углов
четырехугольника
равна
следовательно,
— вписанный.
Тогда
как углы, опирающиеся на одну дугу описанной около
этого четырехугольника окружности.
Рассмотрим треугольники и
В них
и
Значит,
по двум углам. Запишем отношение
подобия:
По теореме Пифагора для прямоугольного треугольника
Тогда так как — центр окружности, то
Таким образом,
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Окружность с центром в точке касается сторон угла с вершиной
в точках
и
Отрезок
— диаметр этой окружности.
а) Докажите, что прямая параллельна биссектрисе угла
б) Найдите если
Источники:
а) Центр окружности, вписанной в угол, лежит на его биссектрисе, так как он
равноудален от сторон этого угла. Тогда — биссектриса угла
Также
центр
лежит на диаметре
Заметим, что как отрезки касательных, проведенных к
окружности из одной точки, а значит, треугольник
— равнобедренный.
Поэтому его биссектриса из вершины
также является и высотой, то есть
При этом как опирающийся на диаметр, а значит,
Таким образом,
и
следовательно,

б) Рассмотрим четырехугольник В нем
так
как радиусы
и
проведенные в точку касания, перпендикулярны
касательным
и
соответственно. Значит, сумма противоположных углов
четырехугольника
равна
следовательно,
— вписанный.
Тогда
как углы, опирающиеся на одну дугу описанной около
этого четырехугольника окружности.
Рассмотрим треугольники и
В них
и
Значит,
по двум углам. Запишем отношение
подобия:
По теореме Пифагора для прямоугольного треугольника
Тогда так как — центр окружности, то
Таким образом,
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Окружность с центром в точке касается сторон угла с вершиной
в точках
и
Отрезок
— диаметр этой окружности.
a) Докажите, что
б) Найдите расстояние от точки до прямой
если известно, что
и
Источники:
а) Центр окружности, вписанной в угол, лежит на его биссектрисе, так как он
равноудален от сторон этого угла. Тогда — биссектриса угла
Также
центр
лежит на диаметре
Рассмотрим четырехугольник В нем
так как
радиусы
и
проведенные в точку касания, перпендикулярны
касательным
и
соответственно. Значит, сумма противоположных углов
четырехугольника
равна
следовательно,
— вписанный.
Тогда
как углы, опирающиеся на одну дугу описанной около
этого четырехугольника окружности.
Таким образом,

б) В прямоугольном треугольнике имеем:
Пусть — точка пересечения
и
Заметим, что
как отрезки касательных, проведенных к окружности из одной точки, а
значит, треугольник
— равнобедренный. Поэтому его биссектриса из
вершины
также является высотой и медианой, то есть
и
Тогда в прямоугольном треугольнике имеем:
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Окружность с центром в точке касается сторон угла с вершиной
в точках
и
Отрезок
— диаметр этой окружности.
a) Докажите, что
б) Найдите расстояние от точки до прямой
если известно, что
и
Источники:
а) Центр окружности, вписанной в угол, лежит на его биссектрисе, так как он
равноудален от сторон этого угла. Тогда — биссектриса угла
Также
центр
лежит на диаметре
Рассмотрим четырехугольник В нем
так как
радиусы
и
проведенные в точку касания, перпендикулярны
касательным
и
соответственно. Значит, сумма противоположных углов
четырехугольника
равна
следовательно,
— вписанный.
Тогда
как углы, опирающиеся на одну дугу описанной около
этого четырехугольника окружности.
Таким образом,

б) В прямоугольном треугольнике имеем:
Пусть — точка пересечения
и
Заметим, что
как отрезки касательных, проведенных к окружности из одной точки, а
значит, треугольник
— равнобедренный. Поэтому его биссектриса из
вершины
также является высотой и медианой, то есть
и
Тогда в прямоугольном треугольнике имеем:
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Окружность с центром в точке касается сторон угла с вершиной
в точках
и
Отрезок
— диаметр этой окружности.
a) Докажите, что
б) Найдите расстояние от точки до прямой
если известно, что
и
Источники:
а) Центр окружности, вписанной в угол, лежит на его биссектрисе, так как он
равноудален от сторон этого угла. Тогда — биссектриса угла
Также
центр
лежит на диаметре
Рассмотрим четырехугольник В нем
так как
радиусы
и
проведенные в точку касания, перпендикулярны
касательным
и
соответственно. Значит, сумма противоположных углов
четырехугольника
равна
следовательно,
— вписанный.
Тогда
как углы, опирающиеся на одну дугу описанной около
этого четырехугольника окружности.
Таким образом,

б) В прямоугольном треугольнике имеем:
Пусть — точка пересечения
и
Заметим, что
как отрезки касательных, проведенных к окружности из одной точки, а
значит, треугольник
— равнобедренный. Поэтому его биссектриса из
вершины
также является высотой и медианой, то есть
и
Тогда в прямоугольном треугольнике имеем:
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Периметр треугольника равен 36. Точки
и
— середины сторон
и
соответственно. Отрезок
касается окружности, вписанной в треугольник
а) Докажите, что
б) Найдите площадь треугольника если
Источники:
а) Пусть
и
По условию
— середина
поэтому
Также
— середина
поэтому
Тогда
— средняя линия треугольника
параллельная
следовательно,
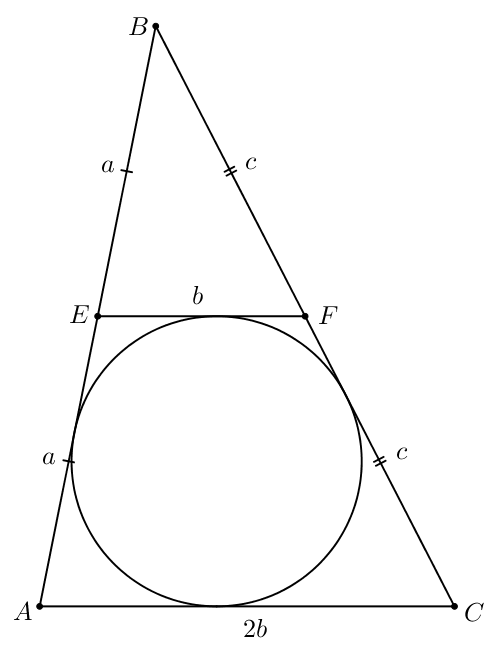
По условию периметр треугольника равен 36, значит,
С другой стороны, касается вписанной окружности треугольника
поэтому четырехугольник
— описанный, следовательно, суммы его
противоположных сторон равны:
Таким образом,
Значит,
б) По условию Тогда запишем теорему Пифагора для
В предыдущем пункте мы доказали, что
Следовательно,
Имеем систему уравнений:

Тогда можем найти площадь прямоугольного треугольника
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Периметр треугольника равен 24. Точки
и
— середины сторон
и
соответственно. Отрезок
касается окружности, вписанной в треугольник
а) Докажите, что
б) Найдите площадь треугольника если
Источники:
а) Пусть
и
По условию
— середина
поэтому
Также
— середина
поэтому
Тогда
— средняя линия треугольника
параллельная
следовательно,
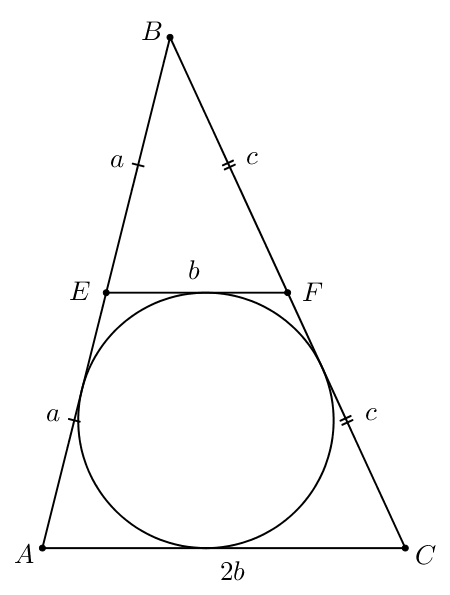
По условию периметр треугольника равен 24, значит,
С другой стороны, касается вписанной окружности треугольника
поэтому четырехугольник
— описанный, следовательно, суммы его
противоположных сторон равны:
Таким образом,
Значит,
б) По условию Тогда запишем теорему Пифагора для
В предыдущем пункте мы доказали, что
Следовательно,
Имеем систему уравнений:

Тогда можем найти площадь прямоугольного треугольника
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В треугольнике угол
равен
Окружность, вписанная в
треугольник, касается стороны
в точке
а) Докажите, что отрезок не больше утроенного радиуса вписанной в
треугольник окружности.
б) Найдите если известно, что отрезок
в 2,8 раза больше
радиуса вписанной в треугольник окружности.
Источники:
а) Пусть — центр окружности,
— точка касания со стороной
Тогда
— отрезок биссектрисы угла
— радиусы.
Следовательно,
откуда
Если
то по
неравенству треугольника
Если то
Следовательно, по итогу Что и требовалось доказать.

б) Рассмотрим
Тогда по теореме
косинусов для этого треугольника имеем
Тогда
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дан остроугольный треугольник В нём провели высоты
и
которые пересеклись в точке
а) Докажите, что угол равен углу
б) Найдите расстояние от центра описанной окружности треугольника
до его стороны
если известно, что
а
Источники:
а) Рассмотрим четырёхугольник Заметим, что он вписанный, так как
сумма его противоположных углов равна
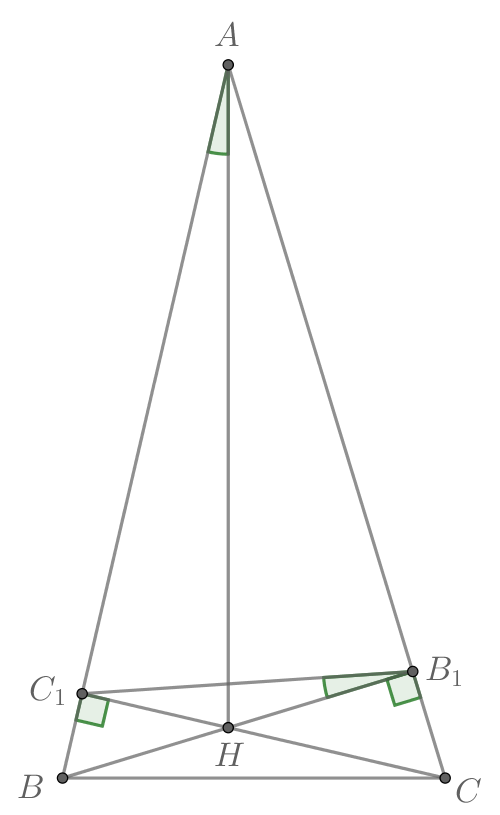
Проведем его диагонали и
Так как
— вписанный, то
углы, опирающиеся на его сторону
равны, то есть
Что и требовалось доказать.
б) Заметим, что с коэффициентом
Докажем
это.
Заметим, что четырехугольник — вписанный, так как углы,
опирающиеся на его сторону
равны
Следовательно, по свойству вписанного четырехугольника.
Угол
общий, значит,
по двум углам с коэффициентом
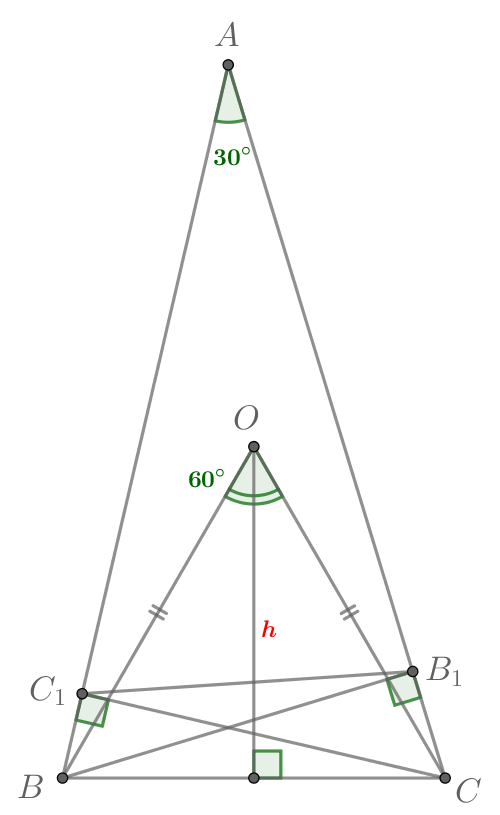
Тогда запишем отношение подобия:
Пусть — центр описанной окружности треугольника
Тогда
центральный угол
в два раза больше вписанного угла
то
есть
Значит, равносторонний, так как в нем есть угол в
и
как радиусы описанной окружности треугольника
Таким
образом,
Тогда расстояние от точки
до
равно высоте равностороннего
треугольника, то есть
б) 18
Ошибка.
Попробуйте повторить позже
Прямая, перпендикулярная стороне ромба
пересекает его диагональ
в точке
а диагональ
в точке
причем
а) Докажите, что
б) Найдите площадь ромба, если
а) Пусть прямая из условия пересекает в точке
а
— в точке
пусть
— точка пересечения диагоналей ромба. Опустим высоту
на
Заметим, что Тогда
Так как а
то
— середина
Запишем теорему Менелая для треугольника и прямой
По теореме Фалеса для угла и параллельных прямых
и
(обе
эти прямые перпендикулярны
)
Таким образом, в два раза меньше
Значит,
Но в ромбе
тогда
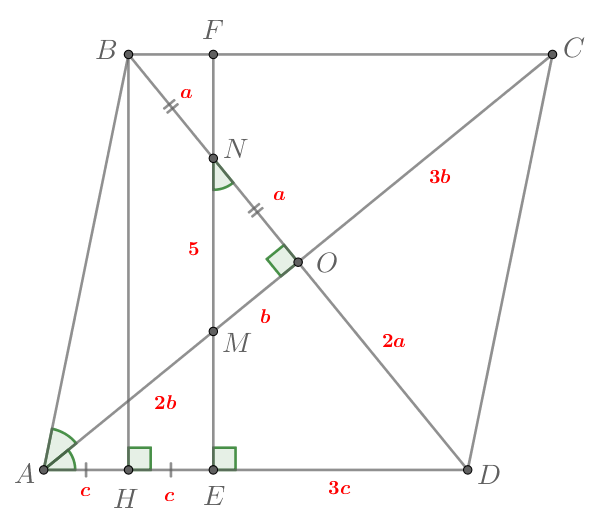
б) Диагонали ромба делят его углы пополам, поэтому
Прямоугольные треугольники и
подобны по двум углам:
прямому и общему. Тогда
Значит, так как то по формуле двойного угла
Тогда
Значит,
Мы знаем, что
Тогда
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана равнобедренная трапеция с основаниями
и
Биссектрисы
углов
и
пересекаются в точке
Точки
и
отмечены на
боковых сторонах
и
соответственно. Известно, что
а) Докажите, что точки
и
лежат на одной прямой.
б) Найдите если известно, что
и
Источники:
а) Так как — биссектриса угла
то
По условию
значит, треугольник
— равнобедренный. Тогда
Таким образом,
Тогда накрест лежащие углы, образованные прямыми и
и секущей
равны. Значит,
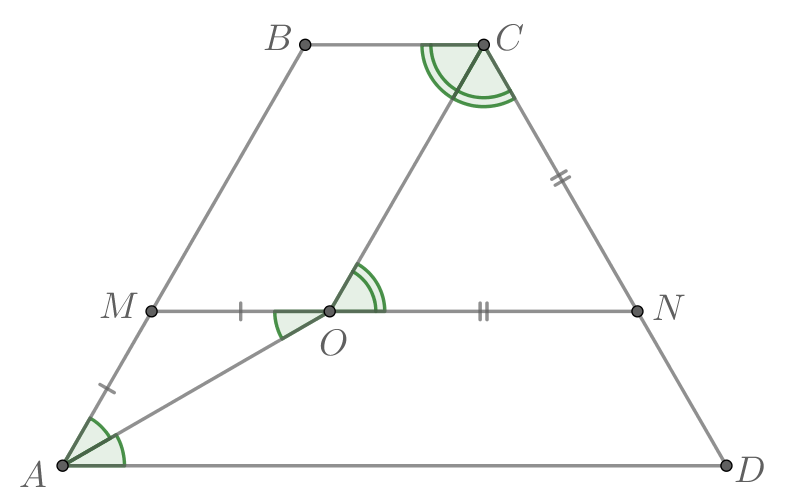
Так как — биссектриса угла
то
По
условию
значит, треугольник
— равнобедренный. Тогда
Таким образом,
Тогда накрест лежащие углы, образованные прямыми и
и секущей
равны. Значит,
Тогда, так как — трапеция, то
Поскольку эти прямые
проходят через точку
то точки
и
лежат на одной прямой. Что и
требовалось доказать.
б) Заметим, что
Опустим из точки перпендикуляры
и
на прямые
и
соответственно. Тогда
Значит,
Тогда прямоугольные треугольники и
равны по гипотенузе и
острому углу, так как
и
Тогда
По пункту а) имеем и
Тогда по теореме Фалеса для
прямых
и
и секущих
и
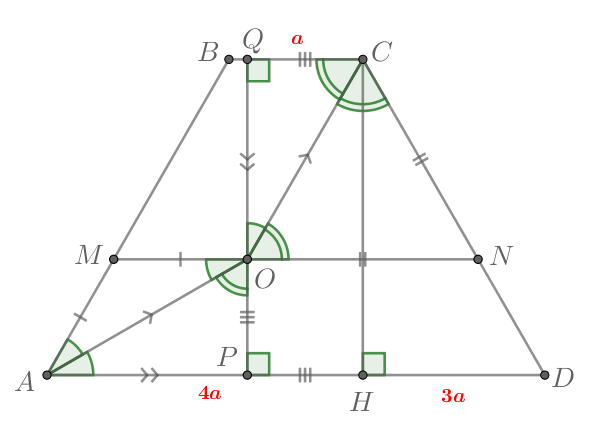
Найдем величину
Пусть — высота трапеции. Тогда
Пусть
Так как трапеция
— равнобедренная,
то
Заметим, что — прямоугольник, тогда
Значит,
получаем
Тогда имеем:
Следовательно,
Так как угол — острый, то получаем искомое отношение
б) 1 : 2
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана равнобедренная трапеция с основаниями
и
Биссектрисы
углов
и
пересекаются в точке
Через точку
провели прямую,
параллельную основаниям, которая пересекла боковые стороны
и
в
точках
и
соответственно.
а) Докажите, что
б) Найдите если известно, что
и
Источники:
а) По условию Тогда
— трапеция. С другой стороны,
трапеция
— равнобедренная, тогда
Значит, — равнобедренная трапеция, то есть
Также из параллельности и
следует, что накрест лежащие углы
и
образованные секущей
равны. Значит,
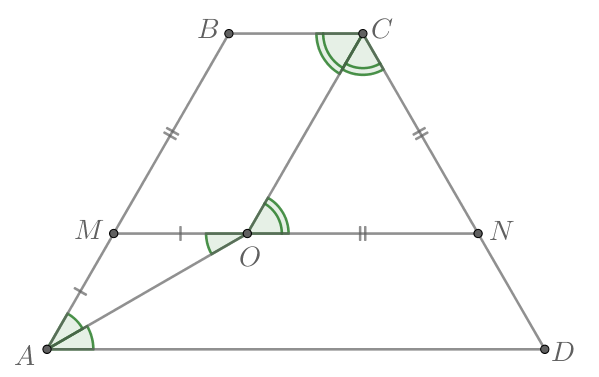
Таким образом, в треугольнике равны углы при стороне
Значит,
он равнобедренный и
Из параллельности и
следует, что накрест лежащие углы
и
образованные секущей
равны. Значит,
Таким образом, в треугольнике равны углы при стороне
Значит,
он равнобедренный и
Таким образом,
б) Заметим, что
Опустим из точки перпендикуляры
и
на
и
соответственно. Тогда
Значит,
Тогда прямоугольные треугольники и
равны по гипотенузе и
острому углу, так как
и
Тогда
По пункту а) и
Тогда по теореме Фалеса для прямых
и
и секущих
и
Значит, Таким образом,
Тогда
— большее
основание.
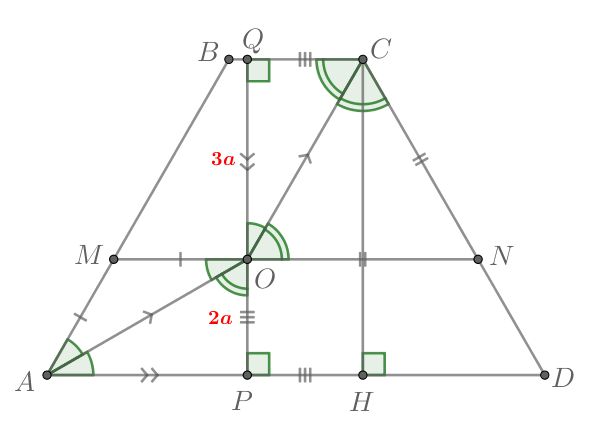
Найдем
Таким образом,
Пусть
Тогда
При этом
— высота трапеции. Пусть
— высота трапеции из
точки
Тогда
Из прямоугольного треугольника
Значит,
Заметим, что — прямоугольник, тогда
Значит,
Таким образом,
Так как трапеция — равнобедренная, то
Следовательно,
Тогда
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дан равносторонний треугольник На его стороне
отмечена точка
Серединный перпендикуляр к отрезку
пересекает стороны
и
в
точках
и
соответственно.
а) Докажите, что угол равен углу
б) Найдите отношение площадей треугольников и
если
а) Треугольник — равносторонний, поэтому все его углы равны
Пусть Тогда
Точки
и
лежат на
серединном перпендикуляре к
поэтому
и
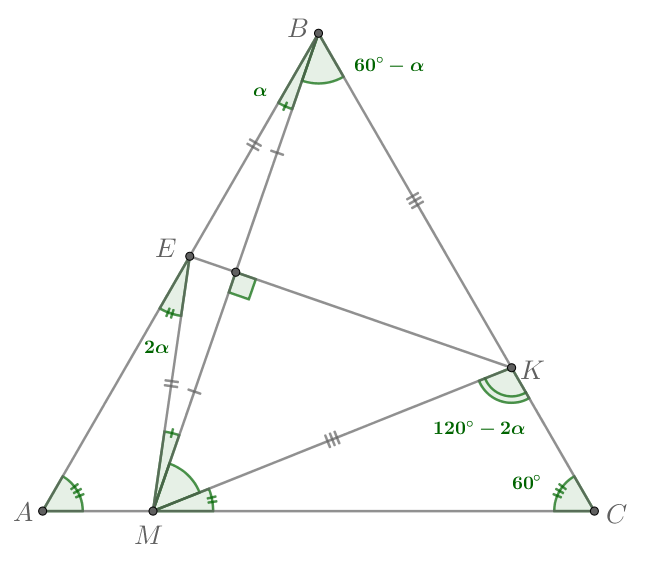
Таким образом, треугольники и
— равнобедренные. Тогда
Заметим, что — внешний для треугольника
поэтому
Аналогично — внешний для треугольника
поэтому
Тогда по сумме углов треугольника
б) Заметим, что треугольники и
подобны по двум углам, так
как
по пункту а),
Тогда
Пусть Тогда, так как
то получаем
Пусть Тогда
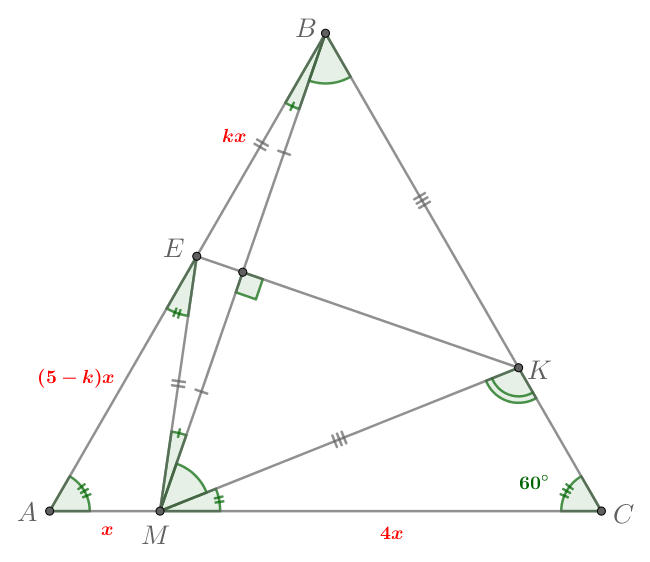
Запишем теорему косинусов для треугольника
Тогда а
Таким образом,
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Прямая, перпендикулярная стороне ромба
пересекает его диагональ
в точке
а диагональ
— в точке
При этом
а) Докажите, что
б) Найдите площадь ромба, если
а) Пусть прямая из условия пересекает в точке
а
— в точке
Пусть
— точка пересечения диагоналей ромба. Опустим высоту
на
Заметим, что Тогда
Так как а
то
— середина
Запишем теорему Менелая для треугольника и прямой
Прямые и
перпендикулярны прямой
а значит параллельны.
Тогда по теореме Фалеса для угла
Таким образом, в два раза меньше
Значит,
Но в ромбе
тогда имеем:
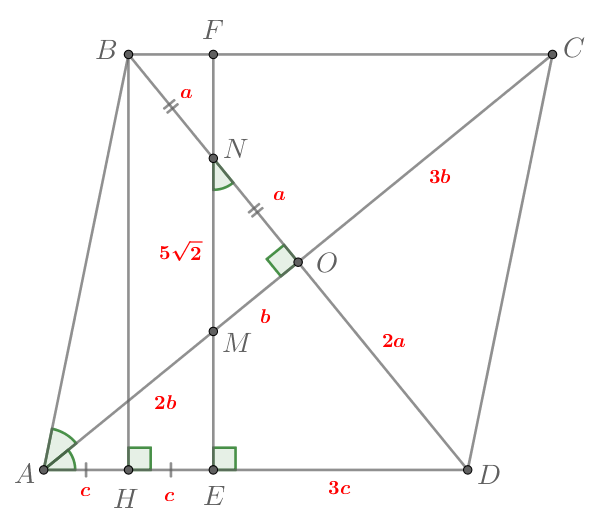
б) Диагонали ромба делят его углы пополам, поэтому
Прямоугольные треугольники и
подобны по двум углам:
прямому и общему. Тогда имеем:
Значит, так как то по формуле косинуса двойного угла
Отсюда получаем
Значит,
Мы знаем, что
Тогда окончательно имеем:
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Прямая, перпендикулярная стороне ромба
пересекает его диагональ
в точке
а диагональ
в точке
причем
а) Докажите, что прямая делит сторону ромба
в отношении
б) Найдите сторону ромба, если
Источники:
а) Пусть прямая из условия пересекает в точке
а
— в точке
пусть
— точка пересечения диагоналей ромба. Опустим высоту
на
Заметим, что Тогда
Так как а
то
— середина
Запишем теорему Менелая для треугольника и прямой
По теореме Фалеса для угла и параллельных прямых
и
(обе
эти прямые перпендикулярны
)
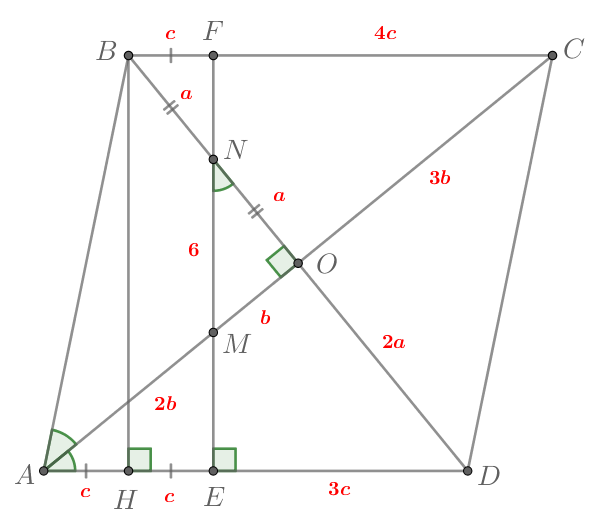
Таким образом, в два раза меньше
Значит,
Значит,
Четырехугольник — прямоугольник. Тогда
следовательно,
б) Заметим, что
Диагонали ромба делят его углы пополам, поэтому
Прямоугольные треугольники и
подобны по двум углам:
прямому и общему. Тогда
Значит, так как то по формуле косинуса двойного угла
Тогда
Значит,
Пусть Тогда по теореме косинусов для треугольника
Таким образом, сторона ромба равна 6.
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |



