Ошибка.
Попробуйте повторить позже
Дан куб . Диагонали основания
и
пересекаются в точке
. Найдите сечение куба плоскостью
,
проходящей через точку
перпендикулярно прямой
.
1) Если , то прямая
перпендикулярна двум пересекающимся прямым, лежащим в плоскости
Построим эти две
прямые.
Рассмотрим содержащую прямую плоскость
Проведем в ней прямую
Теперь необходимо через
точку
их пересечения провести еще одну прямую перпендикулярно
Рассмотрим для этого содержащую прямую плоскость
Проведем через точку
прямую
Так
как по теореме о трех перпендикулярах
как наклонная
— проекция), то
2) Проведем прямые и
. Они могут пересечь либо ребра
и
, либо их продолжения. Так как от этого зависит
вид сечения, определим расположение точек
и
.
Обозначим ребро куба за Тогда
Рассмотрим прямоугольный Так как
, то по свойству прямоугольного треугольника

Тогда с привлечением теоремы Пифагора имеем:
Так как , то
Аналогично
Заметим, что с коэффициентом подобия 2, так как
Следовательно,
Аналогично
Таким образом, получили линии пересечения плоскостей и
с плоскостью
— прямые
и
3) Так как плоскости и
параллельны, то плоскость
пересечет их по параллельным прямым.
Следовательно, в плоскости
через точку
нужно провести прямую, параллельную
.
Так как и
— середины
и
, то
.
Таким образом, сечение куба плоскостью — это четырехугольник
являющийся ромбом, так как
и
Ошибка.
Попробуйте повторить позже
Дан куб , точка
— середина ребра
. Постройте сечение куба плоскостью
, проходящей через точки
и
параллельно диагонали
.
Так как , то прямая
параллельна некоторой прямой, лежащей в плоскости
. Рассмотрим плоскость
, в которой находится прямая
.
Так как , то проведем в этой плоскости
. Тогда по теореме Фалеса точка
— середина
.
Так как — куб, то точка
является точкой пересечения диагоналей квадрата
. Отсюда
и
— искомое сечение куба плоскостью
.
Ошибка.
Попробуйте повторить позже
Дан прямоугольный параллелепипед , в основании которого лежит квадрат
.
На ребрах
,
,
отмечены точки
соответственно так, что
,
,
.
Найдите отношение отрезков, на которые делит плоскость диагональ
.
Обозначим ребро основания за , а боковое ребро за
. Тогда из условия задачи следует, что
,
,
.
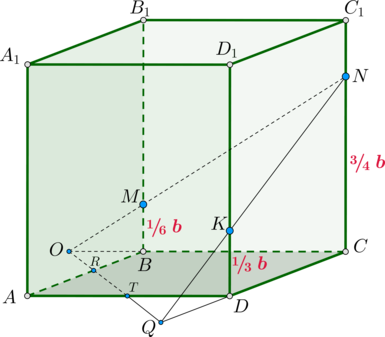
Найдем положение точек и
, в которых плоскость пересекает ребра
и
соответственно.
1) Продлим отрезки и
до пересечения в точке
. Тогда
.
Следовательно,
Аналогично из получаем, что
Соединив точки и
, получим точки пересечения плоскости с ребрами
и
.
2) Рассмотрим основание.
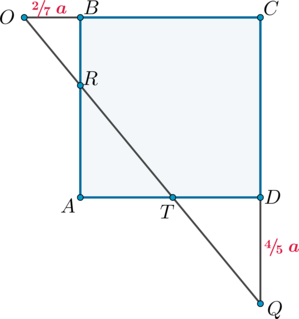
, следовательно,
, следовательно,
3) Для того, чтобы найти, в каком отношении поделит
, проведем прямую
,
.
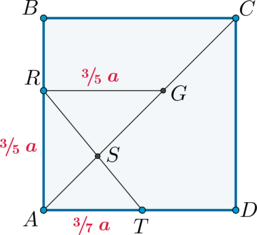
Тогда – прямоугольный и
, то есть он равнобедренный и
.
Тогда по теореме Фалеса
, следовательно, т.к.
, то
.
, следовательно,
Тогда и
.
Ошибка.
Попробуйте повторить позже
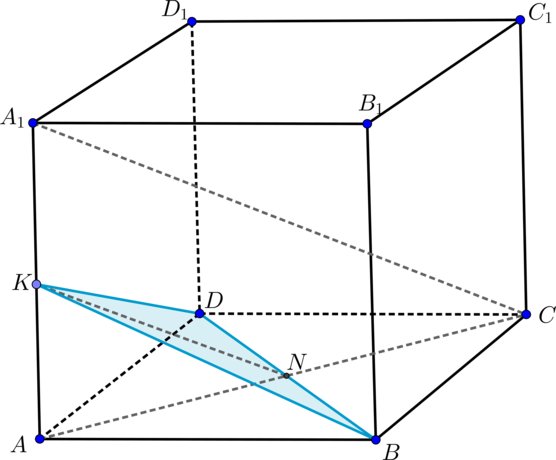
Дан куб На ребрах
и
отмечены точки
и
соответственно, причем
а
—
середина
Найдите сечение куба плоскостью
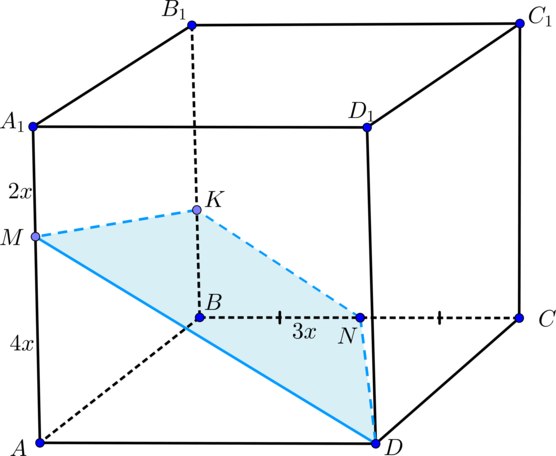
Так как грани и
куба параллельны, то плоскость
пересечет их по параллельным прямым. Тогда
проведем
и получим
— искомое сечение.
Необходимо найти точное расположение точки
Обозначим ребро куба за Тогда
следовательно,
Таким образом,
Ошибка.
Попробуйте повторить позже
Постройте сечение правильной четырехугольной пирамиды, проходящее через точки
и
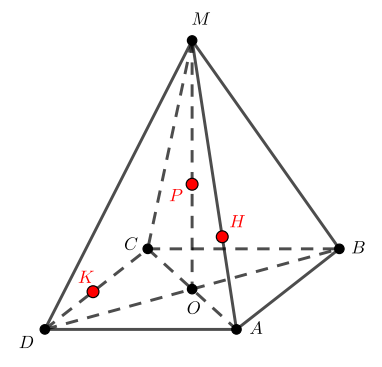
Точки сечения всюду обозначены синим и пронумерованы в том порядке, в котором мы их строим.
Обозначим через плоскость сечения.
- 1.
-
Все точки прямой
принадлежат
при этом
Тогда
и
принадлежат
- 2.
-
Все точки прямой
принадлежат
при этом
Тогда
и
принадлежат
- 3.
-
Все точки прямой
принадлежат
при этом
Тогда
принадлежит
- 4.
-
Искомое сечение
![]()
Ошибка.
Попробуйте повторить позже
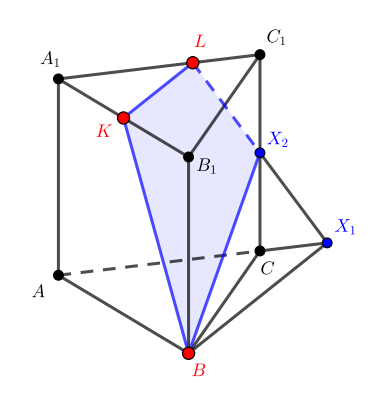
Постройте сечение правильной шестиугольной призмы, проходящее через точки ,
и точку
бокового ребра
.
![]()
Точки сечения, которые мы строим, всюду обозначены синим и пронумерованы в том порядке, в котором мы их строим!
Обозначим через плоскость сечения.
- 1.
- Все точки прямой
принадлежат
, при этом
. Тогда
,
и
принадлежат
.
- 2.
- Все точки прямой
принадлежат
, при этом
. Тогда
принадлежит
.
- 3.
- Все точки прямой
принадлежат
, при этом
. Тогда
принадлежит
.
- 4.
- В правильной шестиугольной призме противолежащие
грани
и
параллельны, следовательно, прямые их пересечения с плоскостью
параллельны.
, тогда прямая через
, параллельная
, принадлежит
и лежит в плоскости
. Ее точки пересечения
и
с ребрами
и
соответственно принадлежат
.
- 5.
- Искомое сечение
.
![]()
Ошибка.
Попробуйте повторить позже
Точка лежит на ребре
треугольной пирамиды
причем
а) Постройте сечение пирамиды плоскостью, проходящей через точку и середины ребер
и
б) В каком отношении плоскость сечения делит ребро
а) Обозначим плоскость сечения через
Все точки прямой принадлежат плоскости
при этом
Тогда
принадлежит плоскости
Все точки прямой принадлежат плоскости
при этом
Тогда
принадлежит
плоскости
Искомое сечение
![]()
б) Запишем теорему Менелая для треугольника и прямой
учитывая, что
Запишем теорему Менелая для треугольника и прямой
учитывая, что
и
Поделив первое на второе, получим
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Точки и
— середины ребер соответственно
и
треугольной призмы
а) Постройте сечение призмы плоскостью, проходящей через точки
и
б) В каком отношении плоскость сечения делит ребро
Обозначим плоскость сечения через
Все точки прямой принадлежат
при этом
Тогда
принадлежит
Все точки прямой принадлежат
при этом
Тогда
принадлежит
Тогда — искомое сечение.
![]()
б) Так как то
по стороне и прилежащим к ней углам. Тогда
Запишем теорему Менелая для треугольника и прямой
учитывая, что
и
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Основание пирамиды — параллелограмм
с центром
. Точка
— середина отрезка
а) Постройте сечение пирамиды плоскостью, проходящей через точку параллельно прямым
и
б) В каком отношении плоскость сечения делит ребро
а) Обозначим через плоскость сечения.
- По условию
, следовательно,
пересекает плоскость
, содержащую прямую
, по прямой, проходящей через точку
и параллельной
. Проведем через
прямую, параллельную
, точки
и
— ее пересечения с
и
соответственно — лежат в плоскости
.
- По условию
, следовательно,
пересекает плоскости
и
, содержащие
, по прямым, параллельным
. Проведем через
и
прямые, параллельные
, тогда
и
— точки пересечения этих прямых с
и
соответственно, эти точки также принадлежат
.
- Все точки прямой
принадлежат
, при этом
. Тогда
принадлежит
.
- Все точки прямой
принадлежат
, при этом
. Тогда
принадлежит
.
Получили, что — искомое сечение.
![]()
б) По построению плоскость сечения параллельна прямой . Отрезок
лежит как в плоскости сечения, так и в
плоскости
, значит, он параллелен
. Тогда по теореме Фалеса
Отрезок равен четверти диагонали
параллелограмма, следовательно, искомое отношение равно
.
б)
Ошибка.
Попробуйте повторить позже
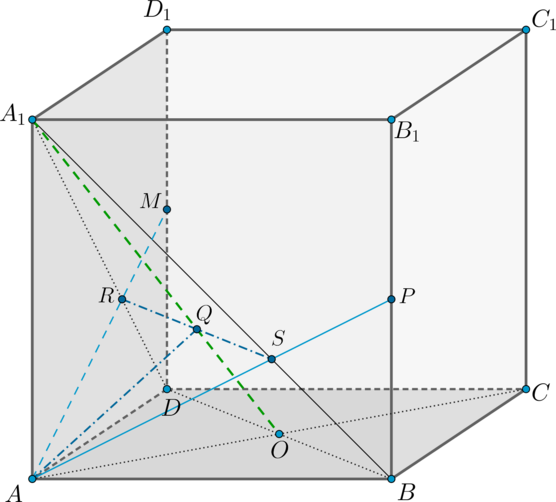
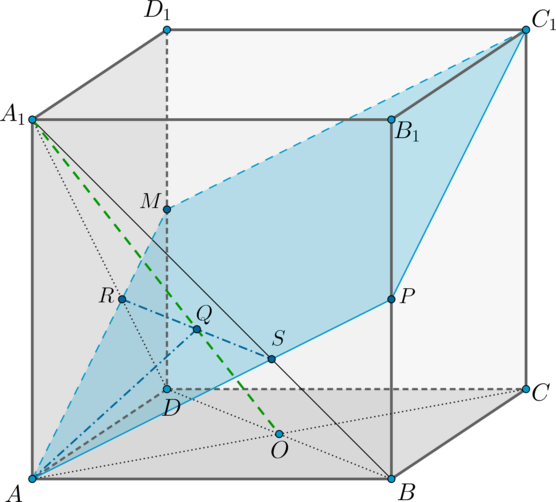
Постройте сечение куба, проходящее через точки
и
а)
![]()
б)
![]()
в) (точка М находится в верхней грани)
![]()
г)
![]()
Точки сечения всюду обозначены синим и пронумерованы в том порядке, в котором мы их получаем.
а) Обозначим через плоскость сечения.
- 1.
-
Все точки прямой
принадлежат
при этом
Тогда
и
принадлежат
- 2.
-
Все точки прямой
принадлежат
при этом
Тогда
и
принадлежат
- 3.
-
Все точки прямой
принадлежат
при этом
Тогда
и
принадлежат
- 4.
-
Искомое сечение
![]()
б) Обозначим через плоскость сечения.
- 1.
-
Все точки прямой
принадлежат
при этом
Тогда
принадлежит
- 2.
-
Все точки прямой
принадлежат
при этом
Тогда
и
принадлежат
- 3.
-
Все точки прямой
принадлежат
при этом
Тогда
принадлежит
- 4.
-
Искомое сечение
![]()
в) Обозначим через плоскость сечения. Считаем, что
- 1.
-
Все точки прямой
принадлежат
при этом
Тогда
принадлежит
- 2.
-
Все точки прямой
принадлежат
при этом
Тогда
принадлежит
- 3.
-
В кубе плоскости
и
параллельны. Тогда прямые их пересечения с плоскостью
должны быть параллельны между собой. Таким образом, прямая пересечения плоскостей
и
должна быть параллельна прямой
а также должна проходить через точку
(так как
и
Тогда точка
(такая, что
принадлежит
- 4.
-
Все точки прямой
принадлежат
при этом
Тогда
принадлежит
- 5.
-
Искомое сечение
![]()
г) Обозначим через плоскость сечения.
- 1.
-
Все точки прямой
принадлежат
при этом
Тогда
и
принадлежат
- 2.
-
Все точки прямой
принадлежат
при этом
Тогда
принадлежит
- 3.
-
Все точки прямой
принадлежат
при этом
Тогда
принадлежит
- 4.
-
Искомое сечение
![]()
Ошибка.
Попробуйте повторить позже
Точка — середина ребра
тетраэдра
. Точки
и
лежат на прямых
и
соответственно,
причем
— середина отрезка
, а
— середина отрезка
.
а) Посторойте сечение тетраэдра плоскостью, проходящей через точки ,
и
.
б) В каком отношении плоскость сечения делит ребро ?
а) Обозначим через плоскость сечения.
- 1.
- Все точки прямой
принадлежат
, при этом
. Тогда
принадлежит
.
- 2.
- Все точки прямой
принадлежат
, при этом
. Тогда
принадлежит
.
- 3.
- Искомое сечение
.
![]()
б) Запишем теорему Менелая для треугольника и прямой
, учитывая, что
и
б)
Ошибка.
Попробуйте повторить позже
Точка — середина ребра
параллелепипеда
Постройте сечение параллелепипеда плоскостью,
проходящей через точку
параллельно прямым
и
- 1.
-
Обозначим плоскость сечения через
По условию
а значит, пересекает плоскость
по прямой, параллельной
и проходящей через точку
так как
и
Тогда точка
такая, что
принадлежит
- 2.
-
В параллелепипеде плоскости
и
параллельны. Тогда прямые их пересечения с плоскостью
должны быть параллельны между собой и параллельны прямой
так как
Таким образом, прямая пересечения плоскостей
и
должна быть параллельна прямой
а также должна проходить через точку
так как
и
Тогда точка
такая, что
принадлежит
- 3.
-
Искомое сечение
![]()
Ошибка.
Попробуйте повторить позже
Точка — середина ребра
параллелепипеда
. Постройте сечение параллелепипеда
плоскостью, проходящей через точки
,
и
.
Обозначим через плоскость сечения. В параллелепипеде плоскости
и
параллельны. Тогда прямые их пересечения с плоскостью
должны быть параллельны между собой. Таким образом,
прямая пересечения плоскостей
и
должна быть параллельна прямой
, а также
должна проходить через точку
(т.к.
и
). Тогда точка
такая, что
,
принадлежит
. Искомое сечение
.
![]()
Ошибка.
Попробуйте повторить позже
В кубе точки
и
— середины ребер
и
соответственно. Постройте сечение куба
плоскостью
Точки сечения на картинке обозначены синим и пронумерованы в том порядке, в котором мы их строим.
а) Обозначим через плоскость сечения. Пусть
— середина
тогда прямая
является проекцией прямой
на плоскость
поскольку
и
![]()
- 1.
-
Пусть
— точка пересечения прямой
и ее проекции
Тогда точка
лежит в плоскости
и в плоскости
- 2.
-
Все точки прямой
принадлежат
при этом
Тогда точки
и
принадлежат
- 3.
-
Все точки прямой
принадлежат
при этом
Тогда точки
и
принадлежат
- 4.
-
Все точки прямой
принадлежат
при этом
Тогда точка
принадлежит
- 5.
-
Искомое сечение
Ошибка.
Попробуйте повторить позже
В кубе точки
и
— середины ребер
и
соответственно. Постройте сечение куба плоскостью,
содержащей прямую
и параллельной прямой
Пусть точка — середина
точка
— середина
Тогда
как средняя линия в треугольнике
Далее, как средняя линия в треугольнике
Кроме того,
так как
и
— середины
противоположных сторон квадрата
Тогда следовательно, точки
и
лежат в одной плоскости
![]()
Плоскость проходит через прямую
и содержит прямую
параллельную
Следовательно,
и есть
плоскость искомого сечения. Продлив
до пересечения с
получим точку
и сечение
Ошибка.
Попробуйте повторить позже
В правильной шестиугольной пирамиде точки
и
— середины ребер
и
соответственно.
Постройте сечение пирамиды плоскостью
Точки сечения всюду обозначены заглавными латинскими и пронумерованы в том порядке, в котором мы их
строим.
Обозначим через плоскость сечения. Поскольку
как средняя линия в треугольнике
то плоскость
параллельна прямой
лежащей в плоскости
основания пирамиды. Тогда
пересекает плоскость
по прямой, параллельной
и проходящей через точку
Пусть
— точка пересечения этой
прямой с
Несложно видеть, что
— середина
так как
и
— середина
по
условию.
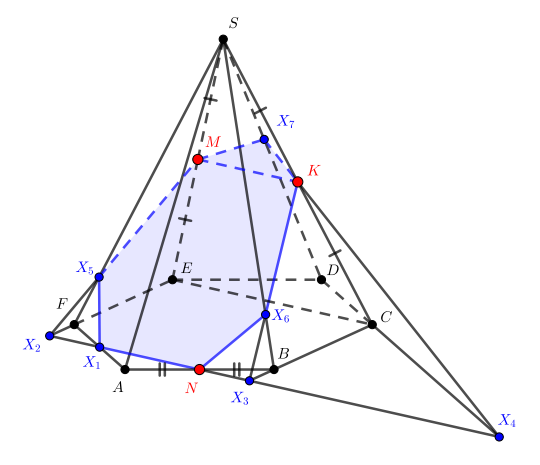
- 1.
-
Все точки прямой
принадлежат
при этом
Тогда
и
принадлежат
- 2.
-
Все точки прямой
принадлежат
при этом
Тогда
принадлежит
- 3.
-
Все точки прямой
принадлежат
при этом
Тогда
принадлежит
- 4.
-
Все точки прямой
принадлежат
при этом
Тогда
принадлежит
- 5.
-
Искомое сечение
Ошибка.
Попробуйте повторить позже
Постройте сечение правильной шестиугольной призмы плоскостью если известно, что сечение представляет собой
четырехугольник.
![]()
Точки сечения всюду обозначены заглавными латинскими и пронумерованы в том порядке, в котором мы их
строим.
Обозначим через плоскость сечения.
![]()
- 1.
-
Все точки прямой
принадлежат
при этом
Тогда
и
принадлежат
- 2.
-
Все точки прямой
принадлежат
при этом
Тогда
и
принадлежат
- 3.
-
Все точки прямой
принадлежат
при этом
Тогда
принадлежит
- 4.
-
Все точки прямой
принадлежат
при этом
Тогда
принадлежит
Заметим, что если
пересечет отрезок
то в сечении получится пятиугольник, что не удовлетворяет условию (последняя вершина сечения будет лежать в таком случае на ребре
).
- 5.
-
Искомое сечение
Ошибка.
Попробуйте повторить позже
Точки ,
и
делят ребра
,
и
правильной четырехугольной пирамиды
соответственно в равных отношениях
. Постройте сечение пирамиды
плоскостью, проходящей через точки
,
и
.
Точки сечения, которые мы строим, всюду обозначены синим и пронумерованы в том порядке, в котором мы их строим!
Обозначим через плоскость сечения.
- 1.
- Все точки прямой
принадлежат
, при этом
. Тогда
принадлежит
.
- 2.
- Все точки прямой
принадлежат
, при этом
. Тогда
принадлежит
.
- 3.
- Все точки прямой
принадлежат
, при этом
. Тогда
и
принадлежат
.
- 4.
- Искомое сечение
.
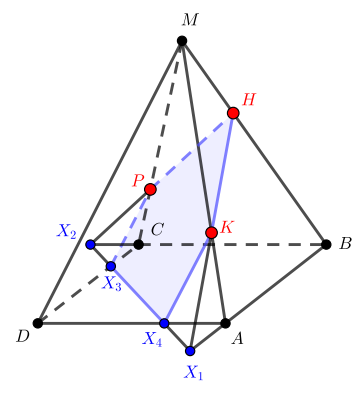
Ошибка.
Попробуйте повторить позже
Точка — центр основания правильной четырехугольной пирамиды
. Точки
и
на отрезках
и
соответственно делят их в равных отношениях
, точка
на ребре
такова,
что
. Постройте сечение пирамиды плоскостью, проходящей через точки
,
и
.
Точки сечения, которые мы строим, всюду обозначены синим и пронумерованы в том порядке, в котором мы их строим!
Обозначим через плоскость сечения.
- 1.
- Все точки прямой
принадлежат
, при этом
. Тогда
принадлежит
.
- 2.
- Все точки прямой
принадлежат
, при этом
. Тогда
принадлежит
.
- 3.
- Все точки прямой
принадлежат
, при этом
. Тогда
принадлежит
.
- 4.
- Все точки прямой
принадлежат
, при этом
. Тогда
и
принадлежат
.
- 5.
- Искомое сечение
.
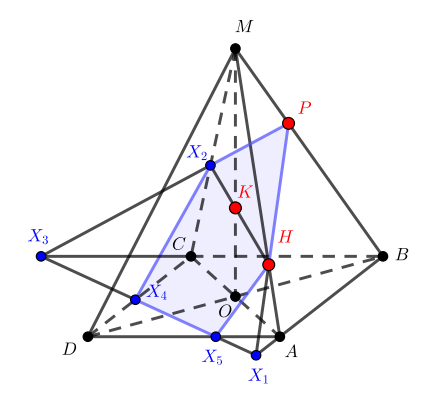
Ошибка.
Попробуйте повторить позже
Дана правильная треугольная призма . Точка
— середина ребра
, точка
делит ребро
в отношении
. Постройте сечение призмы плоскостью, проходящей через точки
,
и
.
Точки сечения, которые мы строим, всюду обозначены синим и пронумерованы в том порядке, в котором мы их строим!
Обозначим через плоскость сечения.
- 1.
- Плоскости
и
параллельны, следовательно, плоскость
сечет их по параллельным прямым. Построим через точку
прямую
, параллельную
. Все точки этой прямой принадлежат
, значит, и
принадлежит
.
- 2.
- Все точки прямой
принадлежат
, при этом
. Тогда
принадлежит
.
- 3.
- Искомое сечение
.