Колебательные системы —Каталог задач по Олимпиадной физике

Ошибка.
Попробуйте повторить позже

Задача 1#45028

Найдите период малых колебаний жидкости в $U$ – образной трубке постоянного сечения. Длина части сосуда, занятой жидкостью, равна $L$ .

Показать ответ и решение

Пусть жидкость в одном из колен поднялась на $x$ , следовательно, в другом она опустилась на $x$ . Тогда возвращающая сила равна

F = ΔpS = 2ρgSx

Масса всей жидкости в сосуде равна

M = ρSl

Тогда из второго закона Ньютона и уравнения гармонических колебаний

2g 2g F = ma = − 2mgx ⇒ a + ---x = 0 ⇒ ω2 = --- L L

А период колебаний

∘ --- T = 2π L-- 2g

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 2#45029

На большой плоской пластине равномерно распределён отрицательный заряд с поверхностной плотностью $σ$ . Однородный стержень массой $m$ и длиной $l$ , по которому равномерно распределён положительный заряд $q$ , вставлен в небольшое отверстие пластины и может двигаться перпендикулярно пластине. Найдите период колебаний стержня. Размеры стержня много меньше размеров пластины. Силы тяжести нет.

Показать ответ и решение

Напряженность направлена к пластине и она равна:

-σ-- E = − 2𝜀 0

Пусть стержень сместится на малое расстояние $x$ , тогда возникнет некомпенсируемый участок с одной стороны расстоянием $2x$ , тогда заряд этого участка $Q = q2x l$ . На этот заряд действует возвращающая сила:

F = QE = − qσx- 𝜀0l

По второму закону Ньютона:

qσ F = max ⇒ max + 𝜀-lx = 0 0

Отсюда

∘ -qσ--- ω = ----- 𝜀0ml

Период

∘ ------ 2π 𝜀 ml T = ---= 2π -0--- ω q σ

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 3#45030

Два груза массами $m1$ и $m2$ , соединённые пружиной жёсткостью $k$ , находятся на гладкой горизонтальной поверхности. Найдите период малых колебаний этой системы.

Показать ответ и решение

Колебания будут происходит около центра масс. Пусть полная длина пружины $l$ , тогда расстояние от каждого груза до центра масса связаны соотношением:

m1- = l2 m2 l1

Кроме того

l1 + l2 = l,

отсюда

---m2---- --m1----- l1 = m1 + m2 l l2 = m1 + m2 l.

Поскольку при колебаниях все витки пружины деформируются одинаково, неподвижный центр масс $C$ как бы "привязан"к одной и той же точке пружины, то есть исходную систему можно рассматривать как два отдельных пружинных маятника.

Поскольку коэффициент жесткости пружины обратно пропорционален её длине, мы можем найти коэффициенты жёсткости частей пружины с длинами $l1$ и $l2$ из соотношений

k1- -l k2- -l k = l ; k = l , 1 2

Следовательно

m + m m + m k1 = k--1-----2, k2 = k --1----2-. m2 m1

Тогда период колебаний:

∘ ---- ∘ ---- ∘ ------------ m1- m2- ---m1m2----- T = 2π k1 = 2π k2 = 2π k(m1 + m2 )

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 4#45031

В глубинах вселенной вдали от всех тяготеющих масс находится тонкий однородный стержень длины $L = 10 м$ и массой $M = 1,0 кг$ . По нему без трения может скользить бусинка массой $m = 0,1 кг$ . В начальный момент бусинка слегка смещена относительно центра стержня и система неподвижна. Через какое время $τ$ бусинка впервые достигнет середины стержня? Гравитационная постоянная $− 11 2 2 G = 6,67 ⋅ 10 Н ⋅ м ∕кг$ .
(Всеросс., 2017, РЭ, 11)

Источники: Всеросс., 2017, РЭ, 11

Показать ответ и решение

В процессе колебаний центр масс системы тел будет оставаться неподвижным. Начало лабораторной системы отсчета $OX$ поместим в центр масс. Подвижную систему отсчета $OX1$ свяжем со спицей. В ЛСО ускорение бусинки при малом ее смещении $x 1$ относительно спицы определяется силой притяжения концевого отрезка спицы длиной $2x1$ и расположенного на расстоянии $≈ L∕2$ от бусинки:

Fx Gm (M ∕L )2x1 8GM am. с =--- = − ----------2--- = − ---3--x1. m m (L∕2) L

Ускорение стержня при этом смещении бусинки

Fx- Gm--(M-∕L-)2x1 8Gm-- aM. c = − M = M (L∕2 )2 = L3 x1.

Тогда ускорение $am$ бусинки относительно стержня будет равно

8G (M + m ) am = am. с − a M. c = −-----------x1. L3

Получено уравнение гармонических колебаний бусинки относительно спицы. Период этих колебаний

∘ ------------- L T = 2π ∕ω = πL ------------. 2G (M + m )

Искомое время равно четверти периода гармонических колебаний

∘ ------------- τ = T- = πL- -----L------ ≈ 2 ⋅ 106 4 4 2G (M + m )

(Официальное решение ВсОШ)

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 5#45032

Бусинка с положительным зарядом $q$ может двигаться без трения по натянутой нити длины $2L$ , на концах которой закреплены положительные заряды $Q$ . Найдите период малых колебаний бусинки, если её масса равна $m$ .

Показать ответ и решение

1. Потенциальная энергия системы зарядов при нахождении бусинки в центре нити:

2qQ- U1 = k L

2. Потенциальная энергия при смещении на $x$

( qQ qQ ) U2 = k ------ + ------ L − x L + x

3. Изменение потенциальной энергии при сдвигании бусинки

( ) -qQ--- --qQ-- 2qQ- ΔU = U2 − U1 = k L − x + L + x − L

4. Упростим, используя $L > > x$

( L2 − Lx + L2 + Lx − 2L2 + 2x2) 2qQx2 ΔU = kqQ --------------2----2------------ ⇒ ΔU = k ---3--- L (L − x ) L

5. В рассматриваемой колебательной системе возвращающей силой является сила электростатического взаимодействия зарядов, при этом квазиупругий коэффициент системы определяется следующим образом:

qQ 2 kx2 qQ ΔU = 2π-𝜀-L3x ≈ -2--⇒ k = π𝜀-L3- 0 0

Циклическая частота равна

( )2 ω2 = 2π- = -g + -kqQ-- T R 8mR3

Откуда

∘ -------3- π𝜀0mL--- T = 2π qQ

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 6#45033

Два маленьких шарика с зарядами $+ q$ каждый надеты на непроводящий вертикальный стержень. Нижний шарик закреплён, а верхний может свободно скользить по стержню. Расстояние между шариками в положении равновесия равно $L$ . Найдите период малых колебаний верхнего шарика. Трением пренебречь. Ускорение свободного падения $g$ .
(«Покори Воробьёвы горы!», 2015, 10–11)

Источники: Покори Воробьёвы горы, 2015, 10–11

Показать ответ и решение

В положении равновесия

kq2- mg − L2 = 0.

При движении верхнего шарика вдоль вертикальной оси

q2 max = k-------2-− mg (L + x )

(ось $x$ направлена вдоль стержня вверх, и начало отсчета совмещено с положением равновесия), и с учетом первого уравнения

kq2 kq2 kq2 x(2L + x ) ----ax = ---------− ----⇒ ax = − g----------. gL2 (L + x)2 L2 (L + x)2

Т.к. колебания малые, то $x < < L$ , и

2g ax ≈ − ---x. L

Частота колебаний в этом случае равна

∘ --- 2g- ω = L ,

а период колебаний

∘ --- T = 2π-= 2π -L-. ω 2g

(Официальное решение ПВГ)

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 7#45034

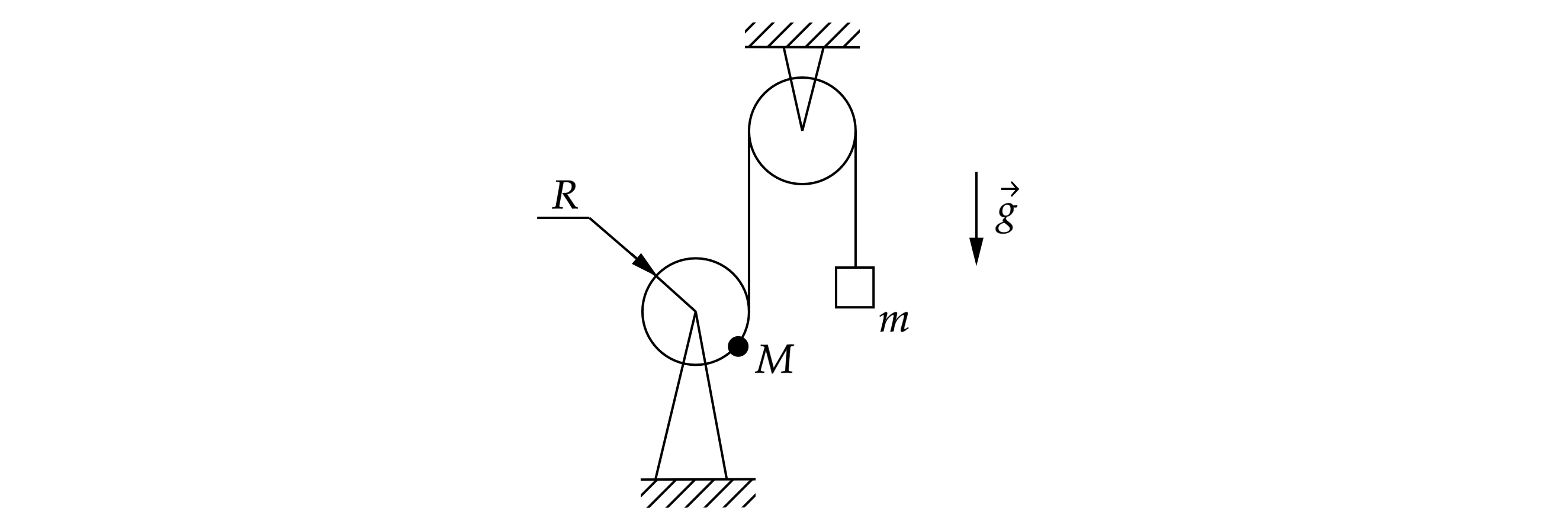
Два лёгких блока соединены нерастяжимой лёгкой нитью (см. рисунок). На краю нижнего блока радиуса $R$ закреплена точечная масса $M$ , соединённая с нитью. К другому концу нити прикреплён груз $m$ , причём $M > m$ . Найдите период $T$ малых колебаний системы около положения равновесия.

(Всеросс., 2013, РЭ, 11)

Источники: Всеросс., 2013, РЭ, 11

Показать ответ и решение

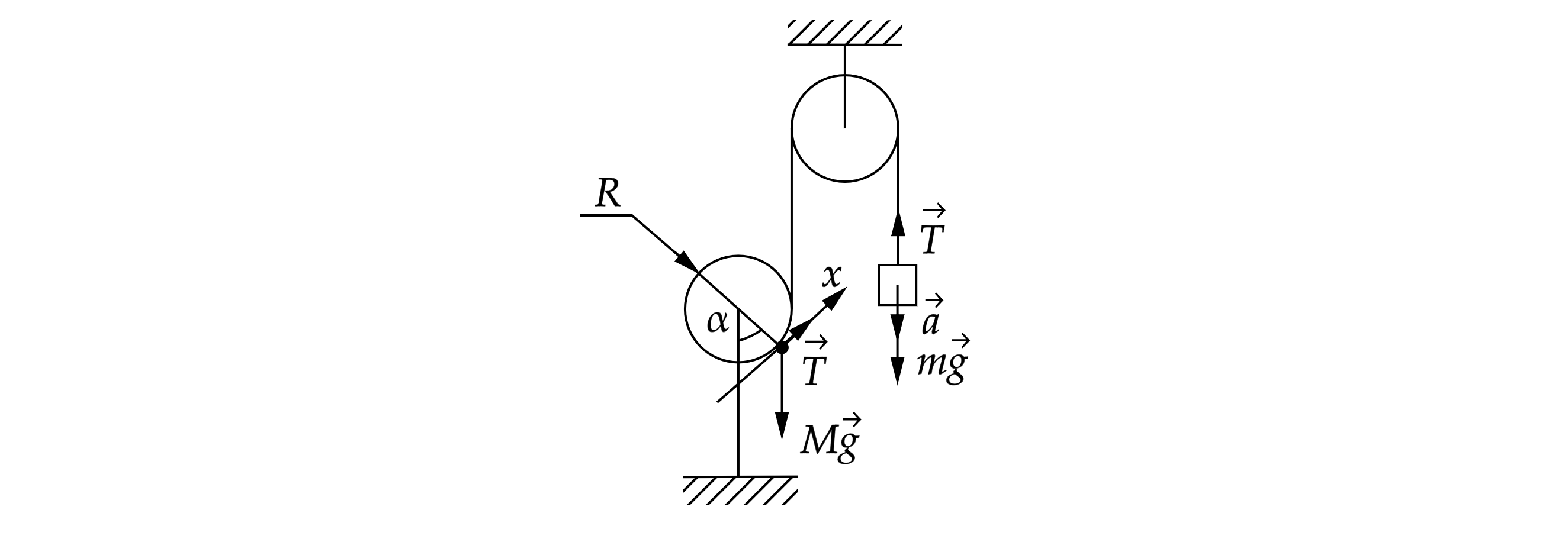
Угол $α0$ , соответствующий положению равновесия, определяется из уравнения:

M gsinα0 = mg. (1)

По второму закону Ньютона для груза $m$ (рис. 17):

ma = mg − T. (2)

По второму закону Ньютона для точечной массы M в проекции на ось Ox:

M a = T − M gsinα. (3)

Так как нить нерастяжимая, то значения ускорений точечной массы $M$ и груза $m$ совпадают. Исключая T из уравнений (2) и (3), получим:

(M + m )a = mg − M g sin α (4)

Масса $M$ закреплена на краю блока, поэтому выполняется соотношение:

a = R ¨α.

Угол $α$ представим в виде:

α = α0 + β, β < < 1,

Тогда

sinα = α cosβ + sinβ cosα ≈ sin α + cosα ⋅ β. (5 0 0 0 0

Подставляя (5) в (4), получим:

(M + m )R ¨α − M g cosα0 ⋅ β.

Учитывая, что $¨ ¨α = β$ , получаем уравнение гармонических колебаний:

¨β + ω2β = 0,

где $∘ ------------ M--gcos-α-- ω = (M + m )R .$ Выразим $cosα0$ из (1). Окончательно получаем:

∘ --∘ -------- T = 2π-= 2π R-4 M--+--m- ω g M − m

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Второй закон Ньютона	2

Записано условие при положении рановесия	2

Сказано, какие ускорения равны	2

Записана формула для ускорения и получено уравнение гаромнических колебаний	2

Представлен правильный ответ	2

Максимальный балл	10

Ошибка.
Попробуйте повторить позже

Задача 8#45035

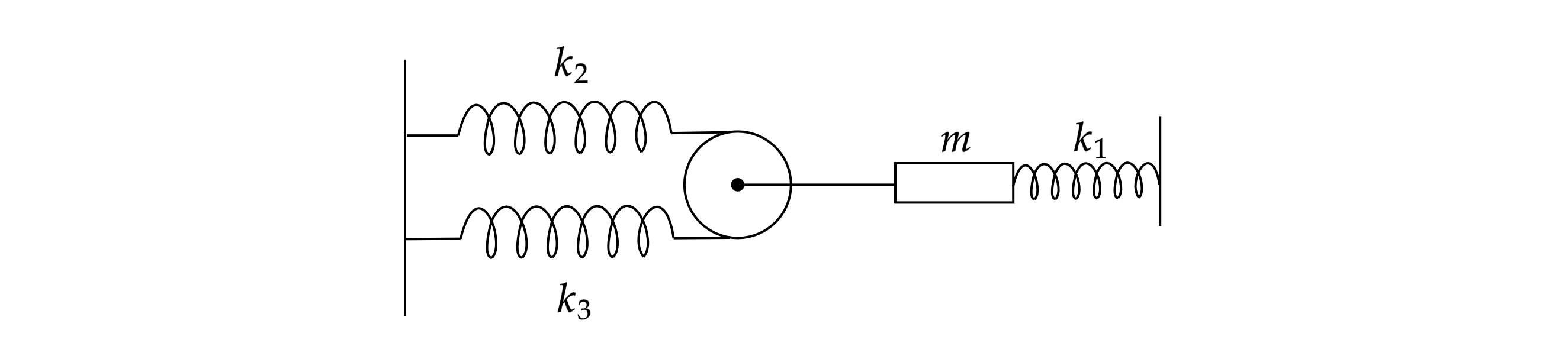
Колебательная система состоит из груза массой $m = 100 г$ , лежащего на гладкой горизонтальной плоскости, невесомого гладкого блока, двух невесомых, нерастяжимых нитей и трёх невесомых пружин жёсткостью $k = 2∕3 Н/ см 1$ , $k = 1∕2 Н/ см 2$ и $k = 1 Н/ см 3$ , соответственно, соединённых так, как показано на рисунке. Центр масс груза лежит на одной горизонтали с прикреплённой к нему нитью и осью пружины $k1$ . В положении равновесия все пружины растянуты. Считая, что нити все время остаются натянутыми, определите круговую частоту $ω$ малых гармонических колебаний груза.
(Ломоносов, 2021, отбор 11)

Источники: Ломоносов, 2021, отбор, 11

Показать ответ и решение

Пусть растяжения пружин в положении равновесия равны $l1$ , $l2$ и $l3$ , соответственно. Тогда сила натяжения пружины $k1$ и правой нити, прикреплённой к грузу, равна $F1 = k1l1$ , а сила натяжения нити, переброшенной через блок, равна $F = k l = k l, 2 2 2 33$ т.к. блок гладкий. Из условия невесомости блока следует, что $F1 = 2F2$ , а поэтому

l = k1-l l = k1-l . 2 2k2 1 3 2k3 1

При смещении груза вправо на расстояние $Δx$ первая пружина сократится на $Δx$ , а вторая и третья удлинятся на $Δx2$ и $Δx3$ , соответственно, причём

Δx + Δx = 2Δx 2 3

т.к. нити нерастяжимы и

k2Δx2 = k3Δx3

т.к. пружины невесомы. Отсюда находим, что

2k 2k Δx2 = ----3--Δx Δx3 = ----2--Δx. k2 + k3 k2 + k3

Изменение потенциальной системы при этом будет

1[ 2 2 2 2 2 2] ΔE = 2 k1 (l1 − Δx ) + k2(l2 + Δx2 ) + k3(l3 + Δx3 ) − k1l1 − k2l2 − k3l3 =

1 [ 2 2 2] = -- (− 2k1l1Δx + 2k2l2Δx2 + 2k3l3Δx3 ) + k1Δx + k2Δx 2 + k3Δx 3 . 2

Иcпользуя записанные выше соотношения между $li$ и $Δxi$ , нетрудно убедиться в том, что выражение в круглых скобках обращается в нуль. Кроме того

4k k2 4k k2 k2Δx22 = ----2-3--2Δx2 l3Δx23 = ----3-2--2Δx2. (k2 + k3) (k2 + k3)

Следовательно,

( ) 1- -4k2k3- 2 ΔE = 2 k1 + k2 + k3 Δx .

Обозначив через $v0$ скорость груза в положении равновесия, по закону сохранения механической энергии имеем

( ) 1 4k2k3 2 mv20 2- k1 + k-+--k- Δx = --2-. 2 3

Поскольку амплитудное значение скорости $v0$ связано с амплитудой смещения $Δx$ соотношением $v = ω Δx 0$ , искомая частота

┌│ ------------- │∘ 4k2k3--+ k1 ω = -k2 +-k3----- m

(Официальное решение Ломоносов)

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 9#45036

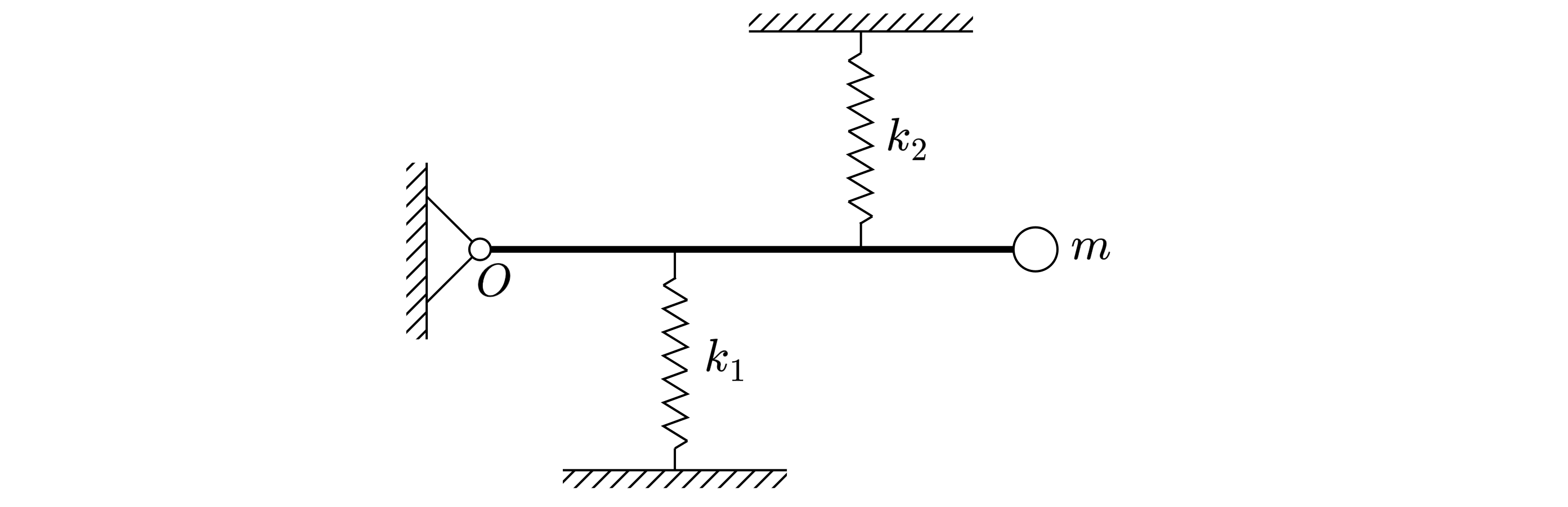
Конструкция из жёстко соединённых лёгкого стержня и небольшого шарика массой $m$ может совершать колебания под действием двух пружин с жёсткостями $k1$ и $k2$ , двигаясь при вращении без трения вокруг вертикальной оси $O$ по гладкой горизонтальной поверхности стола (см. рисунок). Пружины лёгкие, их оси горизонтальны, а точки прикрепления к стержню делят его на три равные части. В положении равновесия оси пружин перпендикулярны стержню, и пружина с жёсткостью $k1$ растянута на величину $L1$ .
1) Найти деформацию второй пружины в положении равновесия.
2) Найти период малых колебаний конструкции.
(МФТИ, 1996)

Источники: МФТИ, 1996

Показать ответ и решение

1) Пусть длина всего стержня $3L$ , так как пружина жёсткостью $k1$ растянута, то сила упругости направлена вниз, следовательно, для равновесия сила упругости пружины $k2$ должна быть направлена вверх. Стержень расположен вертикально. По правилу моментов относительно точки $O$

k L = 2k L ⇒ L = k1L1- 1 1 2 2 2 2k2

Момент силы тяжести равен нулю, так как стержень направлен вертикально.

2) Пусть в некоторый момент смещение шарика от положение равновесия равно $x$

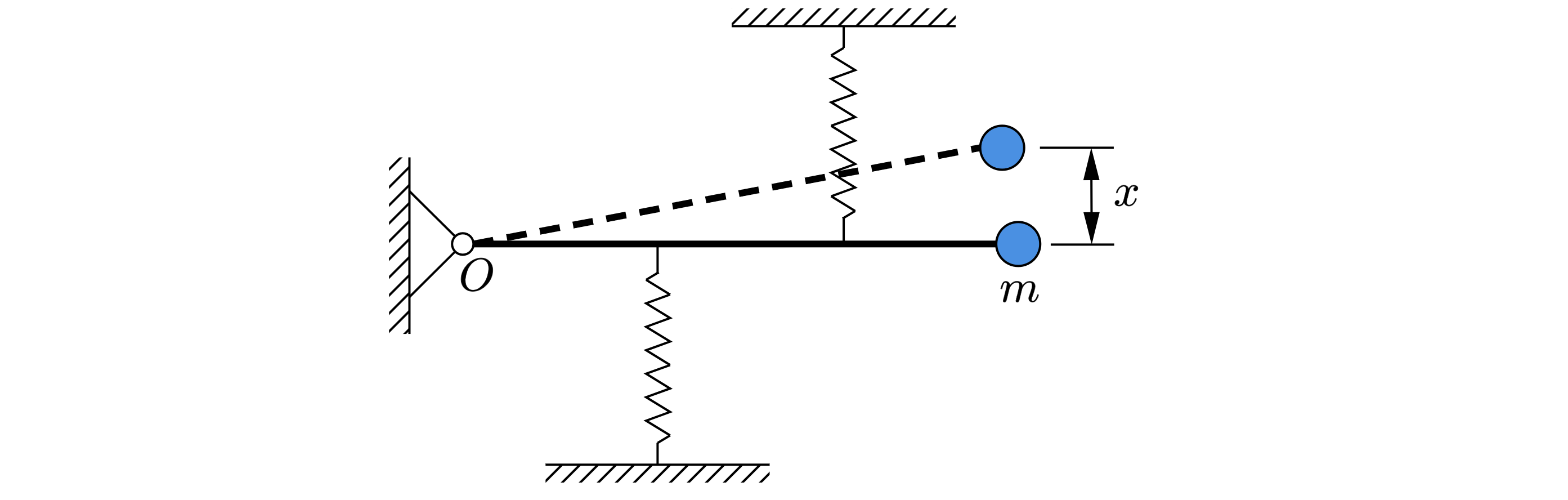
Из подобных треугольников растяжение первой пружины увеличится на $x ∕3$ , а второй уменьшится на $2x ∕3$ . Следовательно, деформация первой пружины равна:

x l1 + --, 3

а второй

2x l2 − --. 3

Потенциальная энергия каждой из пружин

( )2 ( x )2 2x- k1 l1 +-- k2 l2 − 3 E1 = ---------3--, E2 = -------------- 2 2

Кинетическая энергия шарика

mv2 Ek = ----, 2

где $v$ – скорость шарика.
При гармонических колебаниях

E1 + E2 + Ek = const.

Подставив в последнее равенство записанные выше выражения и продифференцировав полученное уравнение по времени, после упрощений получим:

a = − k1-+-4k2-x ⇒ a + k1 +-4k2-x = 0. 9m 9m

Отсюда циклическая частота:

∘ --------- k1-+-4k2- ω = 9m

Период колебаний равен:

2π ∘ ----m---- T = ---= 6π --------- ω k1 + 4k2

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Записано правило моментов	2

Записана деформация первой пружины	2

Записана деформация второй пружины	2

Записан закон сохранения механической энергии	2

Представлен правильный ответ	2

Максимальный балл	10

Ошибка.
Попробуйте повторить позже

Задача 10#45037

Металлический прут в форме дуги окружности радиусом $L$ висит на двух лёгких нитях длины $L$ каждая (см. рисунок). Масса прута равна $m$ , его поперечное сечение постоянно. Угол между нитями равен $2φ$ .
1) Найти силу натяжения нитей в положении равновесия.
2) Найти период малых колебаний такой «дуги» в вертикальной плоскости, совпадающей с плоскостью «дуги».
(МФТИ, 1996)

Источники: МФТИ, 1996

Показать ответ и решение

1) По второму закону Ньютона:

--mg--- T cosφ + T cosφ = mg ⇒ T = 2cos φ.

2) При отклонении на малый угол $α$ возникает некомпенсированный кусочек, на угол $2α$ (будто с другой стороны отрезали кусочек углом $α$ и поставили с другой стороны). Масса $m -α- 2 φ$ Т. к. $α$ мал, то считаем этот кусочек прямым, его центр масс — находящимся в середине. Потенциальная энергия кусочка

α ( ( ( α) ) ( ( α ))) Ep = mg --- = L (1 − cos φ + -- ) − L 1 − cos φ − -- 2φ 2 2

Преобразуем используя косинус суммы и разность

( ) cos φ + α- = cosφ cos(α∕2 ) − sinφ sin(α∕2 ) 2

( α) cos φ − -- = cosφ cos(α∕2 ) + sinφ sin(α∕2 ) 2

Значит

E = mg -α-⋅ 2L sin φ sin(α ∕2) p 2φ

с учетом малости угла $α$ ( $sin(α ∕2) ≈ α∕2$ ), имеем

mgL sin φ 2 Ep = ----------α 2φ

Кинетическая энергия

2 2 ′ 2 E = mv---= mL--(α-)-. k 2 2

Из закона сохранения энергии

Ep + Ek = const

mgL--sin-φ- 2 mL2-(α-′)2- 2φ α + 2 = const

Дифференцируем

g sin φ -------⋅ 2 α ⋅ α′ + L ⋅ 2α′ ⋅ α ′′ = 0 φ

То есть

gsinφ α ′′ + ------α = 0 L φ

Получили уравнение гармонических колебаний, отсюда циклическая частота колебаний:

∘ ------- g sin φ ω = ------- Lφ

и период

∘ ------- T = 2π-= 2π -L-φ--- ω gsinφ

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 11#45038

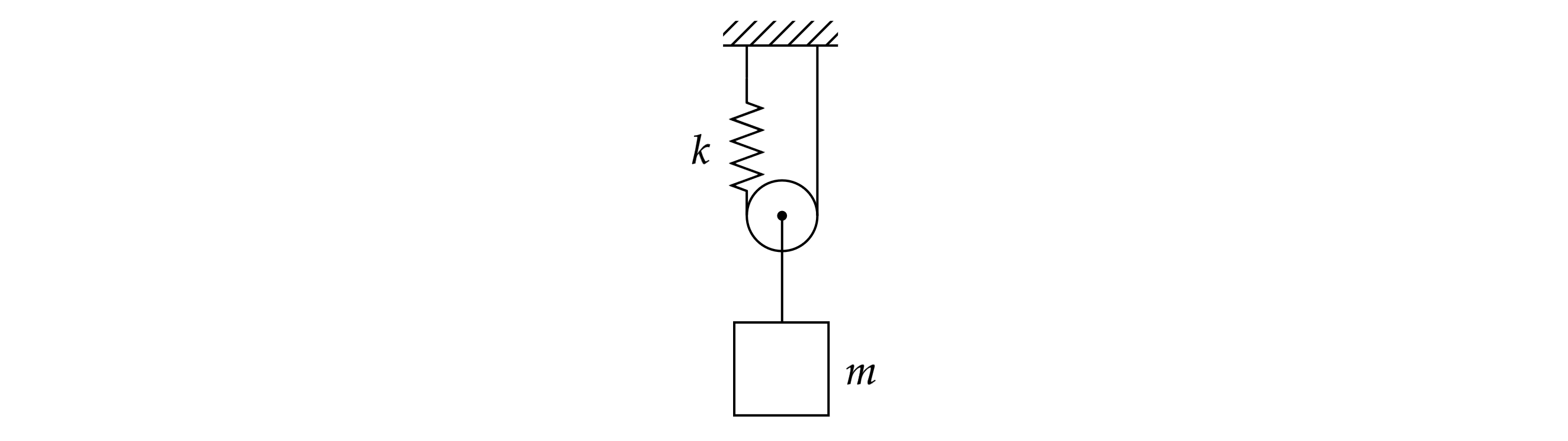
Груз массой $m$ подвешен с помощью пружины жёсткостью $k$ , лёгких нитей и невесомого блока (см. рисунок).
1) Найти удлинение пружины в положении равновесия системы.
2) Найти период вертикальных колебаний груза при условии непровисания нитей.
(МФТИ, 1996)

Источники: МФТИ, 1996

Показать ответ и решение

1) Сила натяжения нити от груза $m$ равна $mg$ , после блока она ”делится на 2 участка”, значит, сила упругости пружины:

F0 = mg--= k Δl0, 2

отсюда искомая величина

mg-- Δl0 = 2k .

2) Пусть длина недеформированной пружины $l 0$ , длина нити – $L 0$ , $Δl$ – деформация пружины. Расставим силы

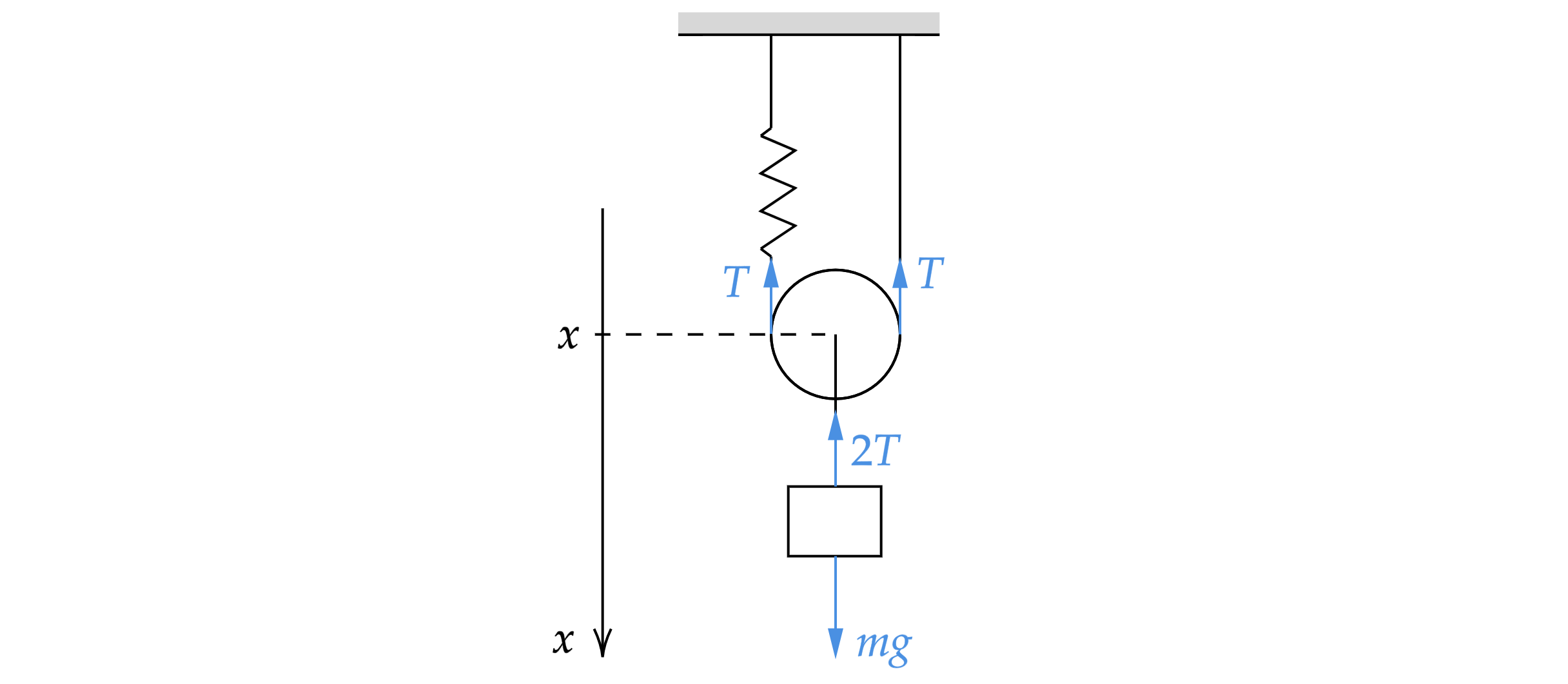
По второму закону Ньютона для груза

max = mg − 2T.

Длина нити и пружины равны:

2x = L0 + l0 + Δl

продифференцируем по времени $t$ дважды:

2ax = 0 + 0 + ¨Δl

С учетом второго закона Ньютона:

¨ m ⋅Δl- = mg − 2kΔl ⇒ Δ¨l + 4kΔl = mg. 2 m

Получили уравнение гармонических колебаний с циклической частотой

∘ --- k- ω = 2 m .

Тогда период

2π ∘ m-- T = ---= π -- ω k

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Записана формула силы упргости пружины	2

Записан второй закон Ньютона	2

Записана деформация пружины	2

Записана формула периода гармонических колебаний	2

Представлен правильный ответ	2

Максимальный балл	10

Ошибка.
Попробуйте повторить позже

Задача 12#45039

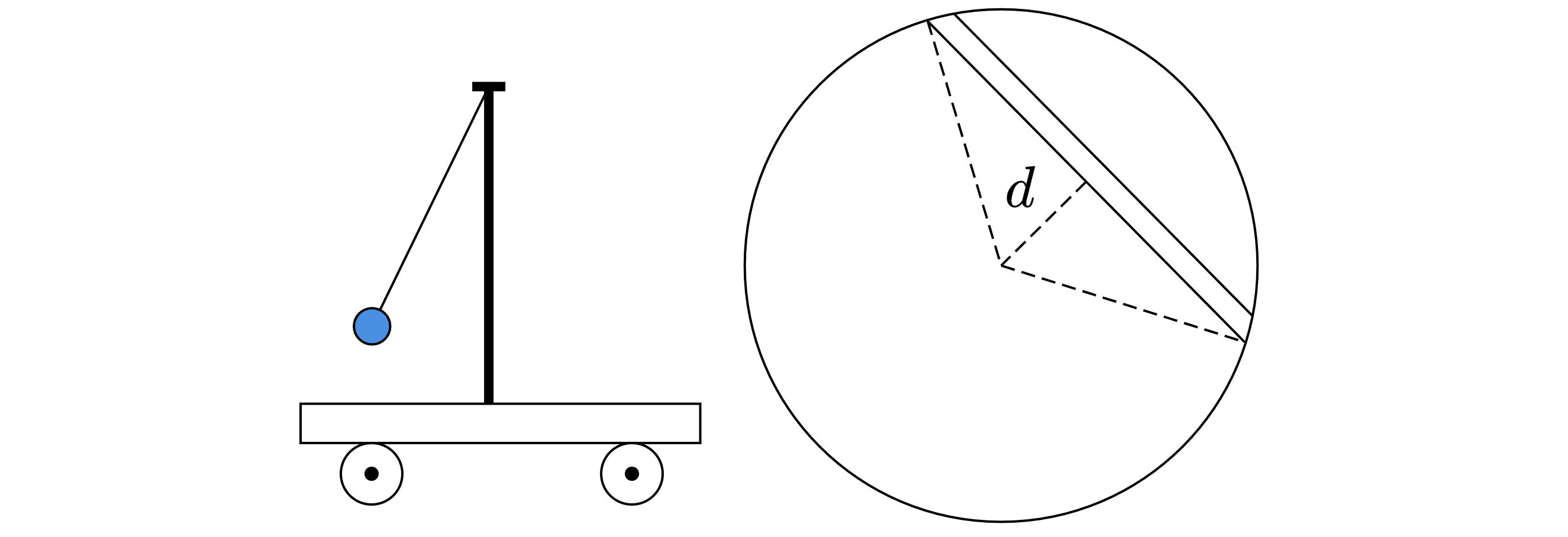
На тележке укреплен математический маятник длины $l$ . Тележку отпускают в туннель, прокопанный внутри Земли по такой хорде, что минимальное расстояние от центра Земли до туннеля равно половине радиуса Земли: $d = R ∕2$ ( $R$ – радиус Земли; см. рисунок). Сколько колебаний совершит маятник за то время, когда тележка пройдет весь туннель? Радиус и масса Земли $R$ и ускорение свободного падения на поверхности Земли известны. Плоскость колебаний маятника совпадает с направлением движения тележки.
(«Росатом», 2020, 11)

Источники: Росатом, 2020, 11

Показать ответ и решение

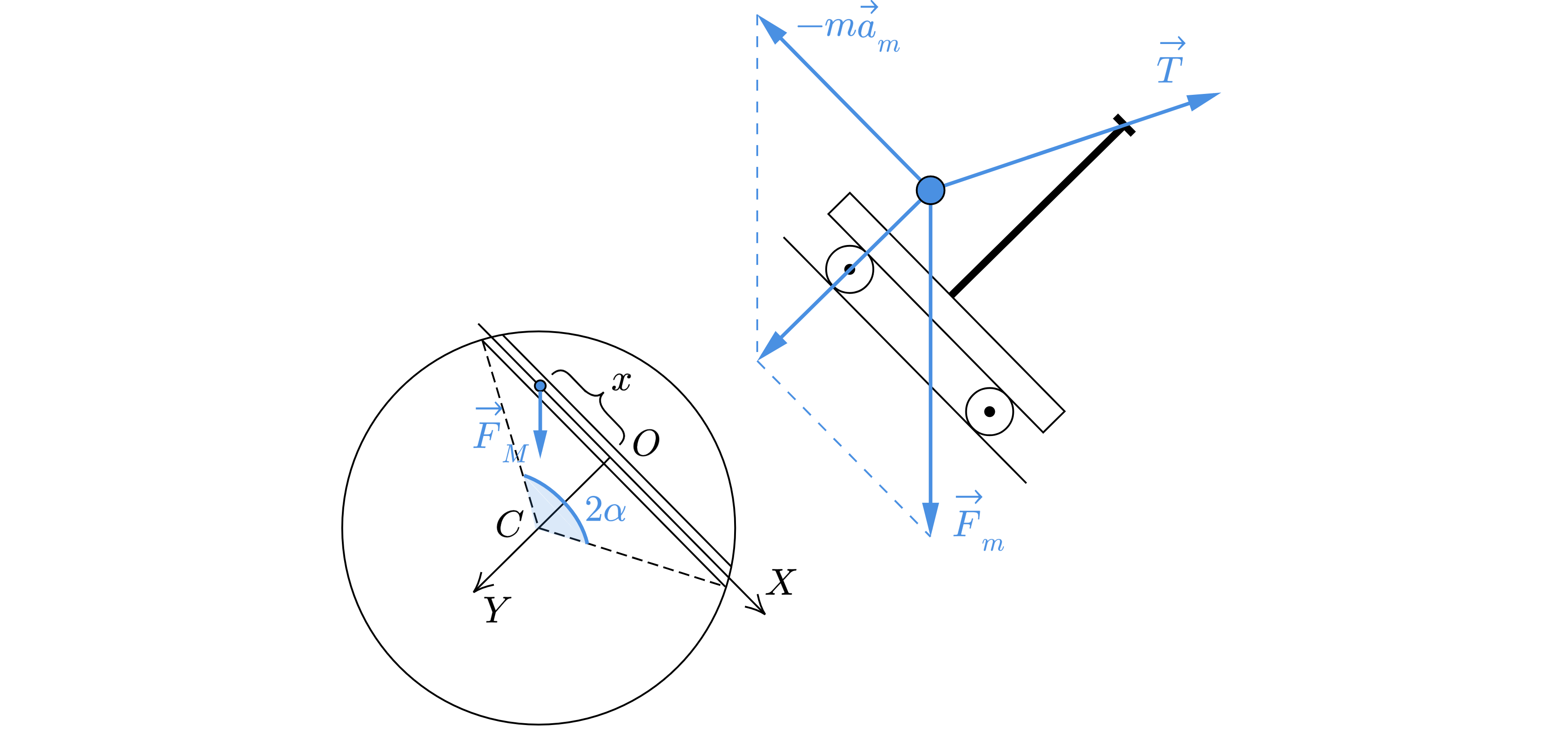
Пусть туннель «опирается» на угол $2 α$ (см. рисунок). Как известно, на тело массой $m$ , находящееся внутри Земли на расстоянии $r$ от ее центра, действует направленная к центру Земли сила тяжести

F = mgr-, m R

где $mg$ – сила тяжести, действующая на тело на поверхности Земли, $R$ – радиус Земли. Применяя второй закон Ньютона к тележке, найдем, что ее ускорение $am$ направлено вдоль туннеля и равно по величине

Fm,x grx am = ----- = ----, (1) m R

где $Fx$ – проекция силы тяжести на ось OX, направленную вдоль туннеля (см. рисунок), $m$ – масса тележки. Поскольку $rx = x$ , из уравнения (1) следует

am − g-x = 0, R

что ускорение тележки пропорционально расстоянию от нее до точки $O$ (ближайшей к центру точки туннеля); это значит, что тележка (вместе с маятником на ней) будет совершать гармонические колебания относительно точки $O$ с периодом

∘ --- R T = 2π --. (2) g

Следовательно, до противоположной точки туннеля тележка доедет за половину периода

--- ∘ τ = π R- (3) g

(причем независимо от того, на какой угол «опирается» туннель). Второй закон Ньютона для маятника имеет вид

m0 ⃗aм = F⃗m + ⃗T,

где $m0$ масса маятника, $⃗a м$ – его ускорение в инерциальной системе отсчета (например, относительно Земли), $T⃗$ – сила натяжения нити. Но поскольку маятник колеблется на тележке, которая движется с ускорением, нам нужно найти его ускорение относительно тележки $⃗aм.о.т.$ . Используя далее, закон, аналогичный закону сложения скоростей (но для ускорений) $⃗a + ⃗a + ⃗a м м.о.т. m$ , получим

m ⃗a = F⃗ + ⃗T − m ⃗a (4) 0 м.о.т. m 0 m

(для знакомых с понятием сил инерции отметим, что уравнение (4) является вторым законом Ньютона в неинерциальной системе отсчета, связанной с тележкой, а $− m ⃗a 0 m$ и есть действующая на маятник сила инерции). Но с учетом (1) величина $m0 ⃗am$ есть проекция действующей на маятник силы тяжести на ось $x$ , поэтому вектор $⃗ Fm − m0 ⃗am$ направлен перпендикулярно туннелю, а его величина равна проекции силы тяжести на ось OY , перпендикулярную туннелю. Поэтому модуль этого вектора равен

| | m gr m gOC ||F ⃗m − m0 ⃗am || = --0--y = --0----- = m0g cos α (5) R R

и не меняется в процессе движения тележки по туннелю (см. рисунок). Из уравнений (4)–(5) следует, что уравнение для ускорения маятника относительно тележки совпадает с уравнением для ускорения математического маятника, но в качестве «силы тяжести» в нем фигурирует постоянная сила $m0g cos α$ . А это значит, что маятник будет совершать колебания с периодом

∘ ------- T = 2π ---l--. m gcos α

Поэтому за время $t$ (3) маятник совершит следующее количество колебаний

∘ -------- ∘ -- ∘ --- N = t-= 1- R-cosα-= 1- d-= 1- -R T 2 l 2 l 2 2l

(Официальное решение Росатом)

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 13#45040

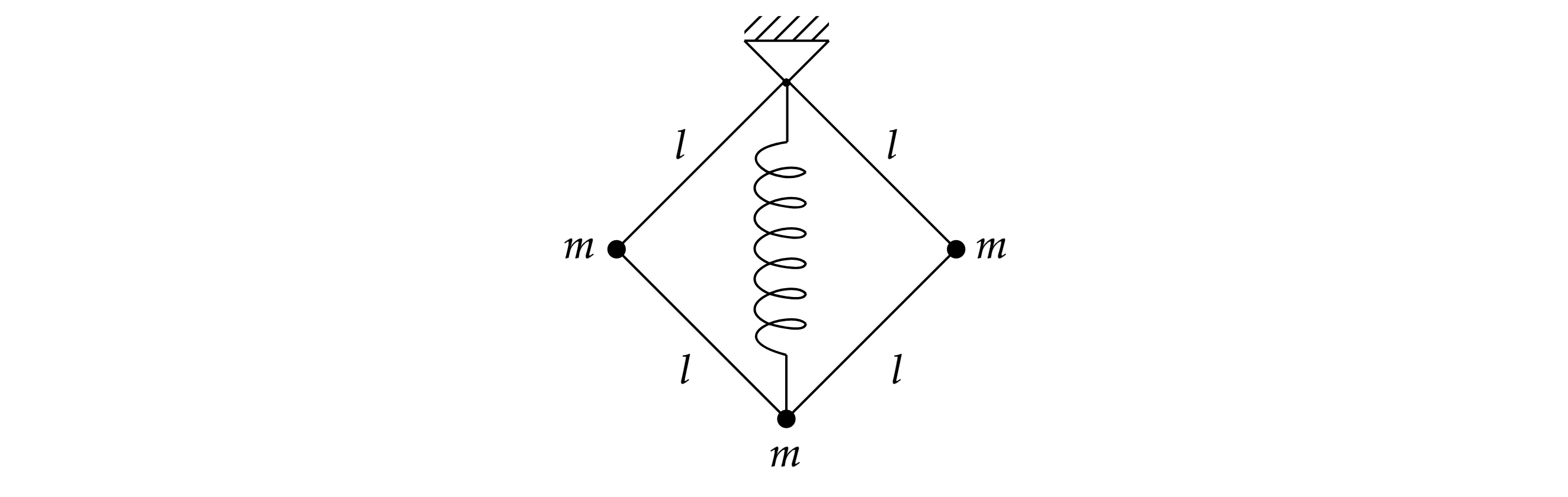
Конструкция (рис.) состоит из трёх одинаковых маленьких шариков массой $m$ каждый, шарнирно соединённых лёгкими спицами длины $l$ . В положении равновесия конструкция удерживается вертикальной пружиной жёсткости $k$ и имеет форму квадрата.
1) Найдите длину $l0$ недеформированной пружины.
2) Пусть нижний шарик смещён по вертикали (вверх или вниз) на малое (по сравнению с $l$ ) расстояние $x$ . Определите изменение $ΔE пот$ потенциальной энергии системы.
3) Пусть нижнему шарику сообщена вертикально направленная скорость $v$ . Определите кинетическую энергию $ΔE кин$ системы.
4) Определите период $T$ малых вертикальных колебаний нижнего шарика.
(Всеросс., 2003, финал, 11)

Источники: Всеросс., 2003, финал, 11

Показать ответ и решение

1. Рассмотрим силы, действующие на "боковые"шарики при равновесии (рис. 17).

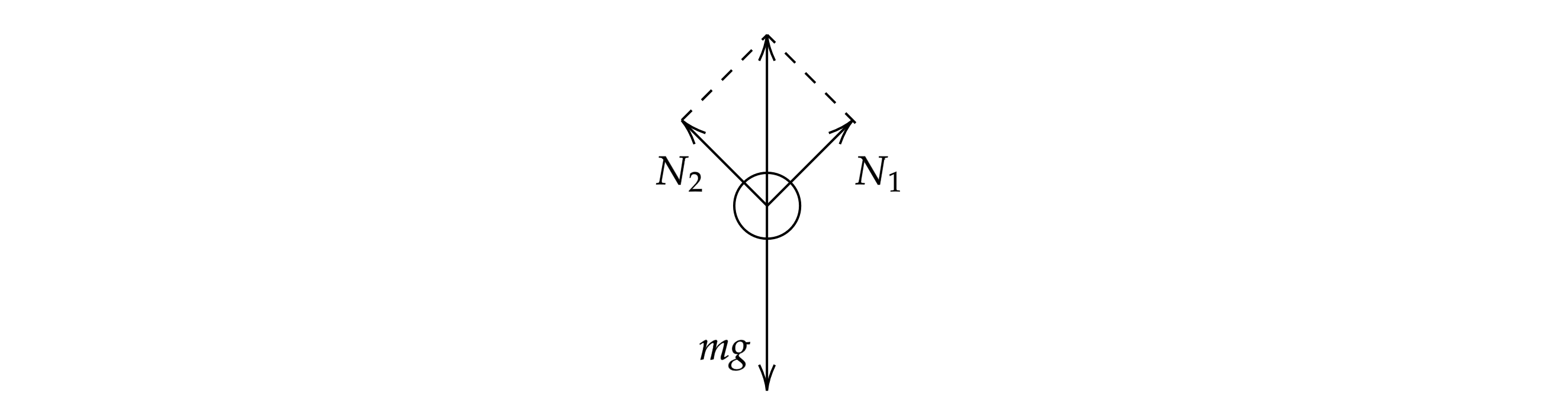
Верхние спицы растянуты, а нижние сжаты по модулю силами. На нижний шарик действует упругая сила пружины $F = 2mg$ (рис. 18)

√ -- kx0 = 2mg ⇒ x0 = 2mg-; l0 = 2l − x0, k

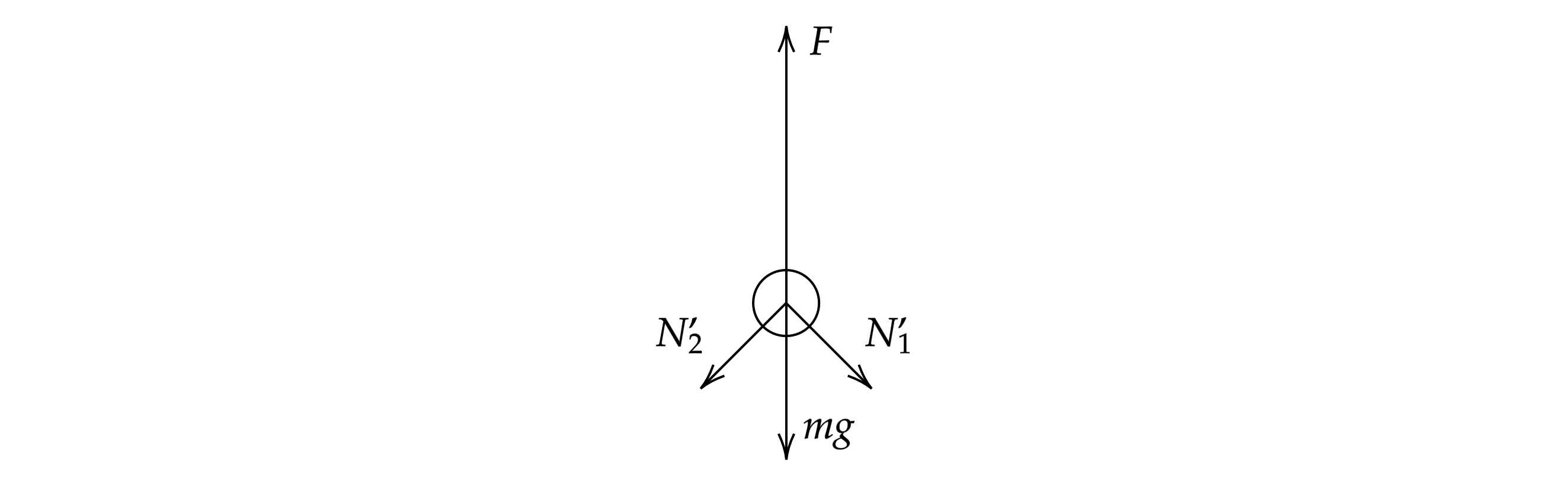
где $x0$ – удлинение пружины.
2. Сместим нижний шарик вниз на расстояние $x < < l$ . Тогда боковые шарики сместятся на $x∕2$ . Изменение потенциальной энергии:

k-(x +-x0)2 kx20- x- kx2- ΔE пот = 2 − 2 − mgx − 2mg 2 = 2 .

3. Пусть нижнему шарику сообщена скорость $v$ , направленная вертикально. Тогда боковые шарики приобретут скорость $v ∕2$ в вертикальном направлении и такую же скорость в горизонталь ном направлении. Полная скорость каждого шарика окажется равной $√ -- √ -- v ⋅ 2∕2 = v∕ 2$ . Следовательно,

2 2 ΔE кин = mv---+ 2 ⋅ mv--= mv2. 2 2 ⋅ 2

4. Изменение энергий:

kx2- 2 2 2 ΔE пот = 2 = Ax ; ΔE кин = mv = Bv ,

откуда

2 A k ω0 = --= ---- B 2m

Период

∘ ---- T = 2π-= 2π 2m-. ω0 k

Докажем формулу:

A ω20 = -- . B

Пусть $x = acos ω0t$ , тогда

v = dx-= − aω sin ω t. dt 0 0

Полная энергия

2 2 2 2 2 2 E = Ax + Bv = Aa cos ω0T + Ba ω0 sin ω0t = const,

не зависит от $t$ . Следовательно,

Aa2 = Ba2 ω2,⇒ ω2 = A-. 0 0 B

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 14#45041

Горизонтально расположенная упругая пружина массой $M$ под действием силы, равной её весу $M g$ , растягивается (или сжимается) на величину $Δx0$ .
1) Чему будет равно удлинение данной пружины, если её подвесить за один конец (без груза)?
2) Чему будет равен период колебаний груза массой $m$ , скреплённого с одним из концов данной пружины, если второй конец пружины неподвижен, а груз скользит по гладкой горизонтальной поверхности?
Деформация пружины во всех случаях мала по сравнению с длиной недеформированной пружины.
(Всеросс., 1997, финал, 11)

Источники: Всеросс., 1997, финал, 11

Показать ответ и решение

Жёсткость данной пружины

M-g-- k = Δx . 0

Найдем жёсткость $k∗$ небольшого элемента этой пружины длиной $dx$ . Если пружина растянута на величину $Δx$ , то очевидно, что удлинение $δx$ элемента пружины длиной $dx$ равно

δx = Δx-dx, l0

где $l0$ – длина пружины, при этом упругая сила в любом сечении пружины равна $F = kΔx$ . С другой стороны, деформация элемента пружины $dx$ может быть записана в виде

δx = -F- = kΔx--. k∗ k∗

Приравняв два выражения дл $δx$ , получим

l k∗ = k -0. dx

1) Рассмотрим вертикально подвешенную пружины (см. рис.).

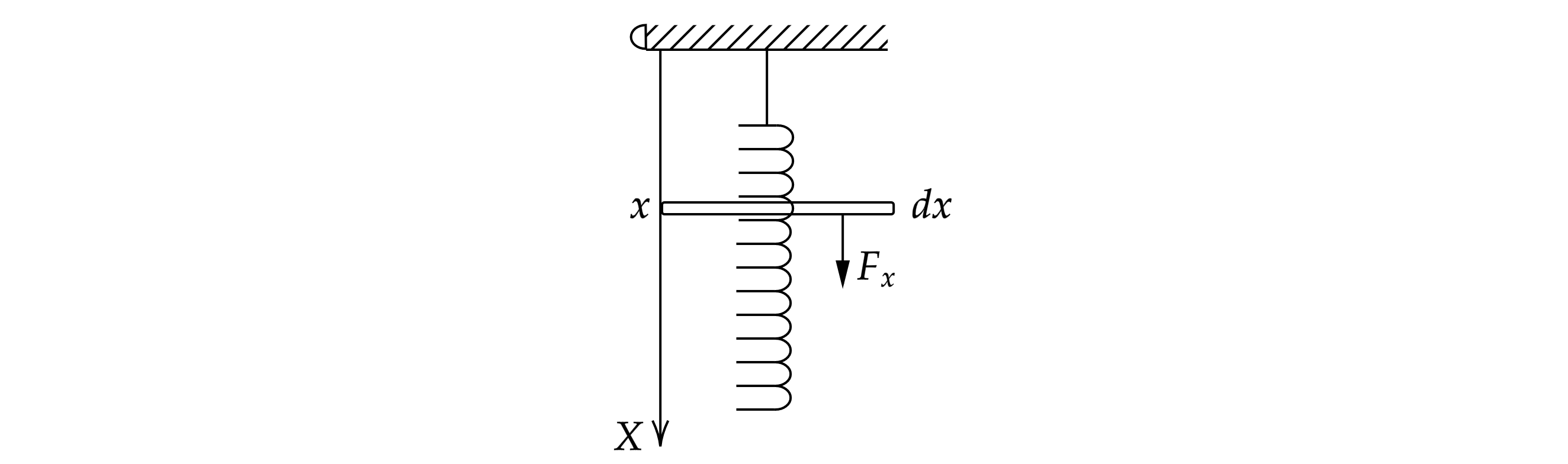
Распределение силы $Fx$ вдоль оси $x$ будет иметь вид

Fx = M--g(l0 − x ) l0

Удлинение элемента пружины длиной $dx$ , имеющего координату $x$ , равно

Fx- M--g(l0-−-x)dx- (l0 −-x-)Δx δx = k∗ − kl2 = l2 dx. 0 0

Очевидно, что удлинение всей пружины

l0 ∫ (l0 − x)Δx0 Δx0 Δx = ------2-----dx = ----. 0 l0 2

2) Пусть в некоторый момент времени груз массой $m$ сместился от равновесного положения ( $x = 0$ ) на величину $x$ (см. рис. 161).

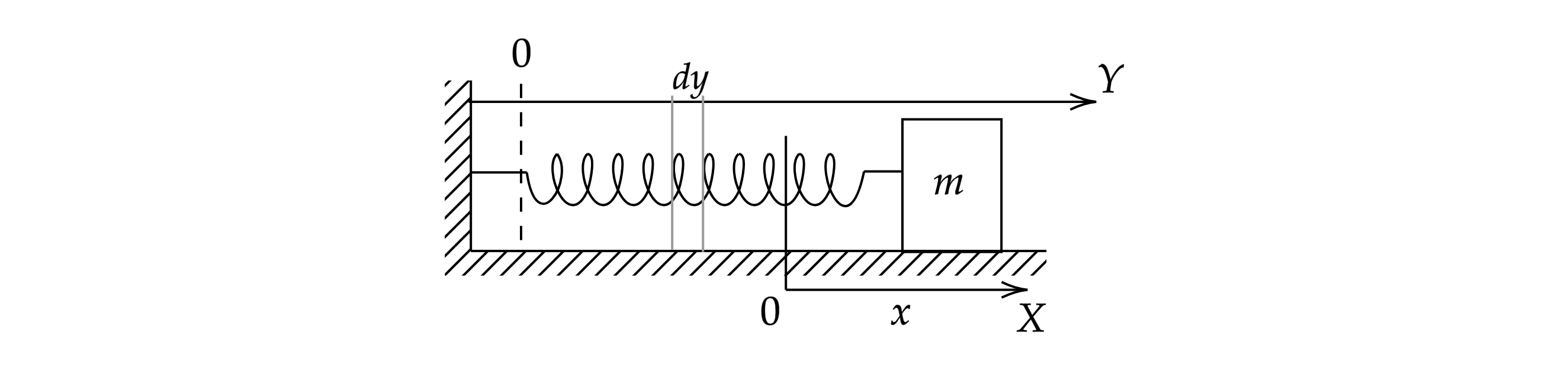
Найдем полную энергию системы "пружина + груз"массой $m$ . Кинетическая энергия груза

mx2 Tm = ----. 2

Если смещение правого конца пружины $x$ , то смещение элемента пружины с координатой $y$ равно

x- xy = l y. 0

Следовательно, скорость элемента пружины с координатой $y$

vy = x˙y = y-˙x0, l0

а кинетическая энергия элемента с длиной $dy$

M y2 M x2 dTпр = ---dy---x˙2 = --3-y2dy. l0 2l0 2l0

Полная кинетическая энергия пружины

∫l0 2 2 Tпр = M-x-y2dy = M-x--. 2l30 6 0

Теперь найдем энергию упругой деформации пружины

2 U = kx--= -M-g-x2. 2 2Δx0

Полная энергия системы "пружина+груз"

2 2 m-˙x-+ m-˙x--+ -M-g--x2 = const. 2 6 2Δx0

Продифференцировав по времени $t$ , получим уравнение движения груза

M g (m + M ∕3)¨x + -----x = 0. Δx0

Период колебания груза:

┌│ (--------)------ │ M-- │∘ m + 3 Δx0 T = 2π ---------------- M g

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 15#45102

Пружина жёсткости $k$ одним концом присоединена к оси колеса массы $m$ , которое способно катиться без проскальзывания, а другим прикреплена к стенке. Найдите период колебаний системы. Масса колеса однородно распределена по ободу.

Показать ответ и решение

При нарушении состояния равновесия система за счёт деформации пружины накапливает энергию, которая при возвращении в состояние равновесия сообщает колесу плоское движение, т.е. поступательное движение его центра масс и вращение точек обода колеса вокруг центра масс.

По закону сохранения энергии

kx2 mv2 J ω2 ----= -----+ ---- 22 22 2 2 2 kx--= m-ω-r--+ J-ω- 2 2 2

Момент инерции колеса $J = mr2$ , поэтому

kx2- 2 2 2 2 = m ω r = mv ∘ ---- v = x -k--= ωx 2m ∘ ---- ω = -k-- 2m

Следовательно

∘ ---- 2m-- T = 2π k

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 16#45103

В глубинах вселенной вдали от всех тяготеющих масс находится тонкий однородный стержень длины $L = 10 м$ и массой $M = 1,0 кг$ . По нему без трения может скользить бусинка массой $m = 0,1 к г$ . В начальный момент бусинка слегка смещена относительно центра стержня и система неподвижна. Через какое время $τ$ бусинка впервые достигнет середины стержня? Гравитационная постоянная $−11 2 2 G = 6,67⋅10 Н ⋅м ∕кг.$
(Всеросс., 2017, РЭ, 11)

Источники: Всеросс., 2017, РЭ, 11

Показать ответ и решение

В процессе колебаний центр масс системы тел будет оставаться неподвижным. Начало лабораторной системы отсчета $OX$ поместим в центр масс. Подвижную систему отсчета $OX1$ свяжем со спицей. В ЛСО ускорение бусинки при малом ее смещении $x 1$ относительно спицы определяется силой притяжения концевого отрезка спицы длиной $2x 1$ и расположенного на расстоянии $≈ L∕2$ от бусинки:

Fx- Gm-(M-∕L)2x1 8GM-- am,C = m = − m (L∕2)2 = − L3 x1.

Ускорение стержня при этом смещении бусинки

F Gm (M ∕L)2x 8Gm aM,C = − -x-= ---------2-1= --3-x1. M M (L∕2) L

Тогда ускорение $am$ бусинки относительно стержня будет равно

a = a − a = − 8G-(M-+-m-)x . m m,C M,C L3 1

Получено уравнение гармонических колебаний бусинки относительно спицы. Период этих колебаний

∘ ----------- L T = 2π∕ω = πL 2G-(M--+-m).

Искомое время равно четверти периода гармонических колебаний

6 τ = T∕4 ≈ 2,0 ⋅10c ≈ 24 суток.

(Официальное решение ВсОШ)

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Отмечено, что при смещении бусинки на $x1$ сила притяжения определяется взаимодействием бусинки и части спицы длиной $2x1$	1

Применены вторые законы Ньютона (по 2 балла за каждый из случаев (для бусинки и для стержня))	4

Получено ускорение бусинки относительно стержня	1

Получено выражение для периода колебаний	2

Получен численный ответ	2

Максимальный балл	10

Ошибка.
Попробуйте повторить позже

Задача 17#45104

В проекте из области фантастики предлагается прорыть между Москвой и Парижем прямолинейный железнодорожный тоннель длиной $L = 2400 км$ . Вагон ставят на рельсы в начале тоннеля в Париже и отпускают без начальной скорости.
1) Через какое время вагон достигнет середины тоннеля?
2) Найдите скорость вагона в середине тоннеля.
Землю считать шаром радиуса $R = 6400 км$ с одинаковой плотностью по всему объёму. Вращение Земли, сопротивление воздуха и все виды трения при движении не учитывать.
(МФТИ, 2003)

Источники: МФТИ, 2003

Показать ответ и решение

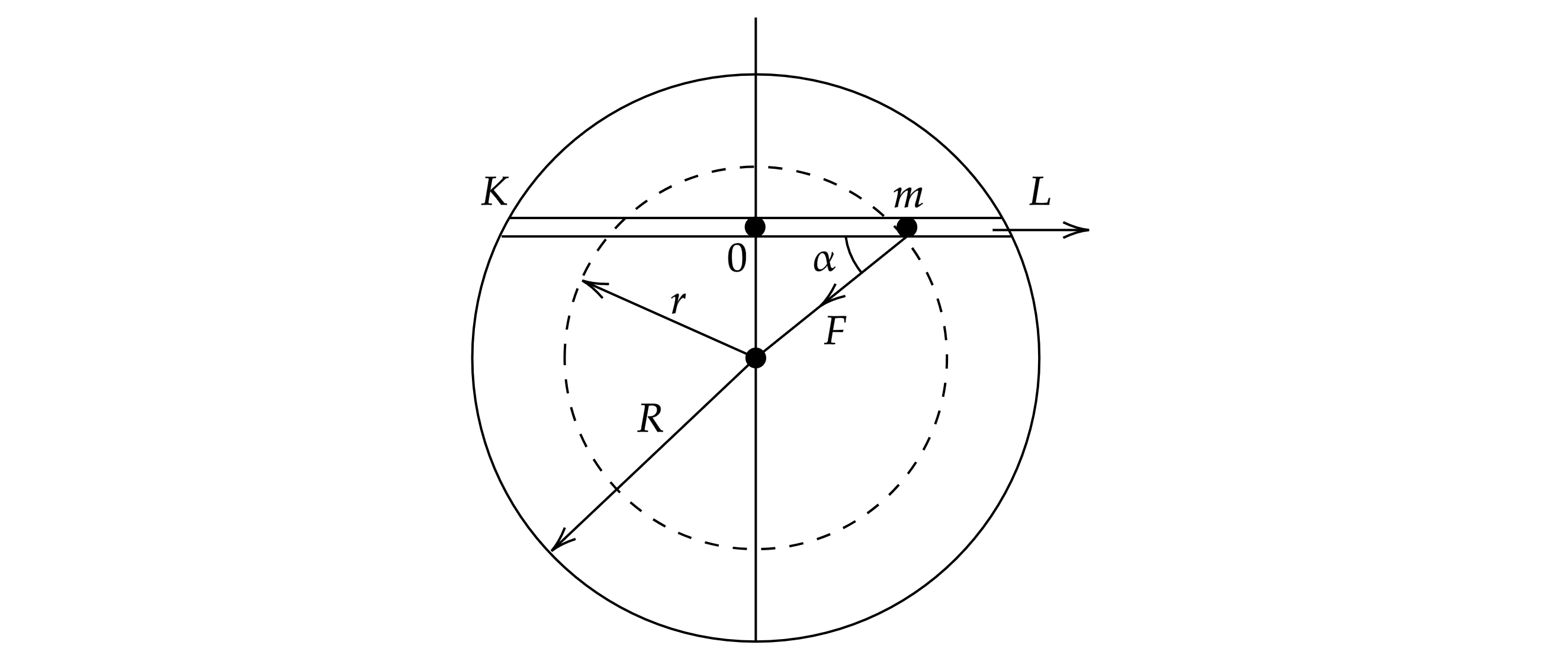
Пусть тело массой $m$ движется по тоннелю в виде хорды KL, изображенному на рис. В некоторый момент времени это тело имеет координату $x$ . В этот момент со стороны Земли на него действует сила тяжести, равная

3 F = GmM----⋅ 4πr-∕3-= GmM---r, r2 ⋅ 4πR3 ∕3 R3

где $M$ - масса Земли, a $r$ - радиус окружности, проходящей через тело массой $m$ . Проекция этой силы на ось х равна

x- GmM---x- -x Fx = − F cos α = − F r = − R3 = − mg R ,

где $g$ - ускорение свободного падения на поверхности Земли. Теперь мы можем записать уравнение движения нашего тела:

m ¨x = − mg x-, R

или

g- ¨x + R x = 0.

Это уравнение описывает гармонические колебания с циклической частотой $ω = ∘g-∕R-$ . Следовательно, наш вагон достигнет середины пути до Парижа через время, равное четверти периода колебаний $(T = 2π ∕ω)$ :